Алгоритми побудови моделей

Модель лінійної регресії (лінійне рівняння) є найпоширенішим видом залежності між економічними змінними.

Скористаймося методом найменших квадратів, суть якого полягає у наступному: сума квадратів відхилень ординат точки, що спостерігається
(X_i, Y_i) від відповідної ординати точки, що лежить на регресійній прямій, повинна бути найменшою

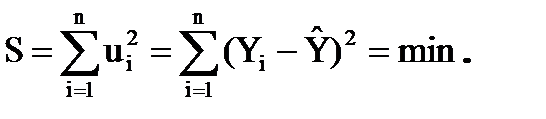
Використання 1МНК для оцінки теоретичних параметрів моделі парної регресії приводить до таких систем нормальних рівнянь:

a) лінійна залежність Y = a₀ + a₁X.

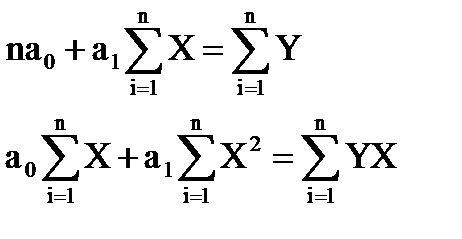
Побудоване лінійне рівняння може слугувати початковою точкою в разі складних (суттєво нелінійних) залежностей.

Нелінійні зв'язки, як правило, певними перетвореннями (заміною змінних чи логарифмуванням) зводять до лінійного вигляду або апроксимують (наближують) лінійними функціями.

б) гіперболічна залежність 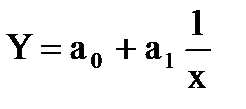. Замінюємо 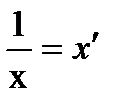і отримаємо лінійну модель Y = a₀ + a₁х′.

Для оцінки теоретичних параметрів моделі складаємо систему нормальних рівнянь:

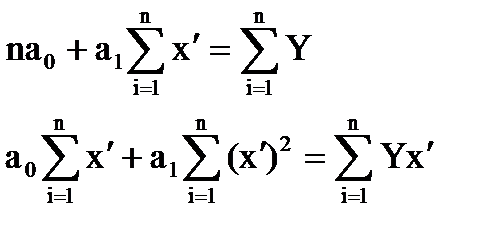
в) параболічна залежність Y = a₀ + a₁х². Замінюємо х² = х′ і отримаємо лінійну модель Y = a₀ + a₁х′.

Для оцінки теоретичних параметрів моделі складаємо систему нормальних рівнянь:

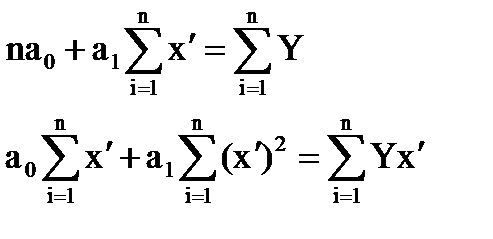
г) степенева залежність .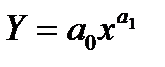

Логарифмуємо функцію lnY = ln a₀ + a₁ · ln Х.

Замінюємо логарифми lnY = Y′, ln Х = Х′, ln a₀ = a′.

Одержуємо лінійну модель Y′ = a′+ a₁ · Х′.

Складаємо систему нормальних рівнянь:

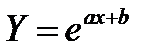д) експоненціальна.

Для оцінки теоретичних параметрів зводимо модель до лінійного вигляду:

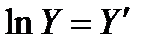Логарифмуємо функцію

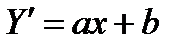Замінюємо логарифм

Одержуємо лінійну модель

е) проста модифікована експоненціальна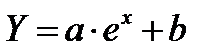

Методом заміни зводимо модель до лінійного вигляду:

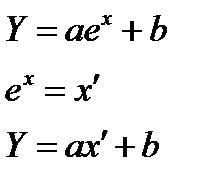
Моделювання здійснюється на основі вибірки статистичних даних, яку студент отримує з відповідних таблиць.

Лабораторні роботи № 1, 2, 3, 4, 5 студент виконує згідно з завданням та варіантом вихідних даних, який отримує у викладача.

Дата добавления: 2015-05-23