Білет№14

N

max ( Rij * Pj),

j = 1

де Pj – імовірність виникнення j-го стану природи (у долях одиниці).

5. Критерій жалю (критерій Севіджа). Використання цього критерію передбачає, що особа, яка приймає рішення, має мінімізувати свої втрати при виборі стратегії. Іншими словами вона мінімізує свою потенційну помилку при виборі неправильного рішення. Використання критерію жалю передбачає:

побудову матриці втрат. Втрати (bij) при цьому розраховуються окремо для кожної стратегії за формулою: bij = max Rij - min Rij;

вибір кращої стратегії за формулою: min (max bij).

Теорія ігор використовується у випадках, коли невизначеність ситуації обумовлена свідомими діями розумного супротивника.

Організації звичайно мають цілі, які суперечать цілям інших організацій-конкурентів. Тому робота менеджерів часто полягає у виборі рішення з урахуванням дій конкурентів. Для вирішення таких проблем призначені методи теорії ігор.

Теорія ігор - це розділ прикладної математики, який вивчає моделі і методи прийняття оптимальних рішень в умовах конфлікту.

Під конфліктом розуміється така ситуація, в якій зіштовхуються інтереси двох або більше сторін, що переслідують різні (суперечні) цілі. При цьому кожне рішення має прийматися в розрахунку на розумного противника, який намагається зашкодити іншому учаснику гри досягти успіху.

Основну задачу теорії ігор можна сформулювати так: визначити, яку стратегію має застосувати розумний гравець у конфлікті з розумним противником, щоб гарантувати кожному з них виграш, причому відхилення будь-кого з гравців від оптимальної стратегії може тільки зменшити його виграш.

Центральне місце в теорії ігор займають парні ігри з нульовою сумою, тобто ігри, в яких:

• приймають участь тільки дві сторони;
• одна сторона виграє рівно стільки, скільки програє інша.

Такий рівноважний виграш, на який мають право розрахувати обидві сторони, якщо вони будуть додержуватися своїх оптимальних стратегій, називається ціною гри. Розв’язати парну гру з нульовою сумою означає знайти пару оптимальних стратегій (одну для першого гравця, іншу – для другого) і ціну гри.

Дві компанії Y і Z з метою збільшення обсягів продажу продукції розробили наступні альтернативні стратегії:

Компанія Y: - Y1 (зменшення ціни продукції);

Y2 (підвищення якості продукції);

Y3 (пропозиція вигідніших умов продажу).

Компанія Z: - Z1 (збільшення витрат на рекламу);

Z2 (відкриття нових дистриб’юторських центрів);

Z3 (збільшення кількості торгових агентів).

Вибір пари стратегій Yi i Zj визначає результат гри, який позначимо як Aij і вважатимемо його виграшем компанії Y. Тепер результати гри для кожної пари стратегій Y i Z можна записати у вигляді матриці, у якій m рядків та n стовпців. Рядки відповідають стратегіям компанії Y, а стовпці - стратегіям компанії Z:

Стратегії Y	Стратегії Z
Z1	Z2	Z3
Y1	А11	А12	А13
Y2	А21	А22	А23
Y3	А31	А32	А33

Така таблиця називається платіжною матрицею гри. Якщо гра записана у такому вигляді, це означає, що вона приведена до нормальної форми.

Для розв’язання гри розраховують верхню і нижню ціну гри та обчислюють сідлову точку.

Нижню і верхню ціну гри знаходимо керуючись принципом обережності, згідно якого у грі потрібно поводити себе так, щоб за найгірших для тебе діях суперника отримати найкращий результат (критерій песимізму).

Нижня ціна гри (яку прийнято позначати ) розраховується шляхом визначення мінімального значення Aij по кожному рядку платіжної матриці (стратегії гравця Y) і вибору з-поміж них максимального значення, тобто:

= max (min Aij).

Верхня ціна гри (яку прийнято позначати 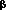) розраховується шляхом визначення максимального значення Aij по кожному стовпцю платіжної матриці гри (стратегії гравця Z) і вибору з-поміж них мінімального значення, тобто:

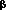= min (max Aij).

Якщо нижня ціна гри дорівнює верхній ( = 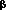), то така гра має сідлову точку і вирішується в чистих стратегіях. Сідлова точка – елемент платіжної матриці гри, який є мінімальним у своєму рядку і одночасно максимальним у своєму стовпці.

Чисті стратегії – це пара стратегій (одна - для першого гравця, а друга - для другого гравця), які перехрещуються в сідловій точці. Сідлова точка в цьому випадку і визначає ціну гри.

Ігри, які не мають сідлової точки, на практиці зустрічаються частіше. У цьому випадку рішення знаходиться в межах змішаних стратегій. Знайти рішення гри без сідлової точки означає визначення такої стратегії, яка передбачає використання кількох чистих стратегій.

Експертні методи прийняття рішень застосовуються у випадках, коли для прийняття управлінських рішень неможливо використовувати кількісні методи. Найчастіше на практиці застосовують такі експертні методи:

• метод простого ранжування;
• метод вагових коефіцієнтів.

Метод простого ранжування (надання переваги) полягає у тому, що кожний експерт позначає ознаки у порядку надання переваги. Цифрою 1 позначається найбільш важлива ознака, цифрою 2 - наступна за ступенем важливості і т.д.

Оцінки ознак (aij) кожного експерта, зводяться в таблицю такого виду:

Ознаки	Експерти
1	2	...	m
x1	a11	a12	...	a1m
x2	a21	a22	...	a2m
...	...	...	...	...
xn	an1	an2	...	anm

Далі визначається середній ранг, тобто середнє статистичне значення Si за і -тою ознакою за формулою:

,

де aij – порядок надання переваги і - тій ознаці j - им експертом;

j - номер експерта;

і - номер ознаки;

m - кількість експертів.

Чим меншим є значення Si, тим вагомішою є ця ознака.

Метод вагових коефіцієнтів (оцінювання) полягає у наданні всім ознакам вагових коефіцієнтів. Воно може здійснюватися двома способами:

1) усім ознакам призначають вагові коефіцієнти так, щоб сума всіх коефіцієнтів дорівнювала 1 або 10, або100;

2) найважливішій з усіх ознак призначають ваговий коефіцієнт, який дорівнює певному фіксованому числу, а решті ознак – коефіцієнти, які дорівнюють часткам цього числа.

Узагальнену думку експертів Si за і -ою ознакою розраховують за формулою:

,

де aij - ваговий коефіцієнт, який призначив j - ий експерт і - ій ознаці;

j - номер експерта;

і - номер ознаки;

m - кількість експертів, які оцінюють і - ту ознаку.

Чим більшою є величина Si, тим більш вагомою є ця ознака.

Дата добавления: 2015-05-23