Введение. Построение кривой свободной поверхности представляет практический интерес и позволяет определить глубины воды в канале с постоянным уклоном дна и в каналах

Построение кривой свободной поверхности представляет практический интерес и позволяет определить глубины воды в канале с постоянным уклоном дна и в каналах, трассируемых по местности с изменяющимися уклонами. Определение глубины в различных сечениях канала позволяет установить размеры затопления берегов при возведении гидротехнических сооружений и решать вопросы о креплении откосов каналов.

В курсовой работе необходимо рассчитать и построить кривую свободной поверхности потока в призматическом канале с изменяющимся уклоном дна.

Курсовая работа состоит из пояснительной записки с необходимыми расчетными таблицами, формулами и графиками, а также продольного профиля канала с нанесенными линиями дна, нормальной, критической и фактической глубин.

Схема системы состоящей из каналов трапециедального и пароболического сечений, соединенных ж/б дюкером.

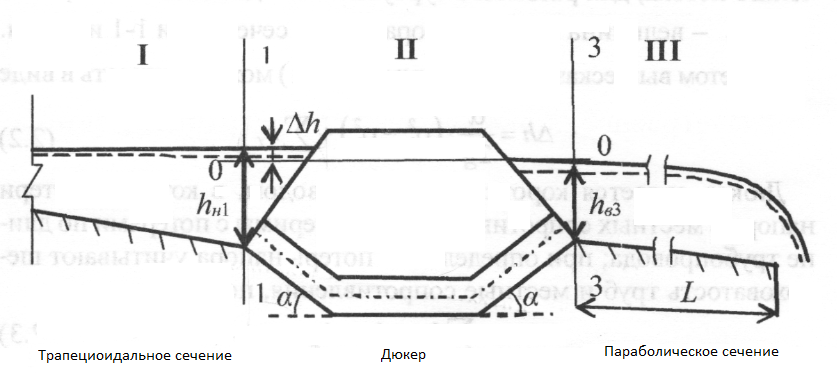
b₁=2,2 м L₂=15 м n₃=0,026

n₁=0,021 α₂=20⁰ i₃=1,3∙10^-4

m₁=1,2 м ∆₂=1,1 мм p₃=1,6 м

i₁=3,4∙10^-4 h_B3=1,7 м

h_н1=2,0 м

1 РАСЧЁТ КАНАЛА ТРАПЕЦЕИДАЛЬНОГО СЕЧЕНИЯ

1. 1 Расчёт нормальной глубины потока

Глубина потока, соответствующая равномерному движению, называется нормальной глубиной и обозначается символом . Основной зависимостью при определении нормальной глубины в данном расчёте является:

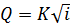, (1.1)

где – модуль расхода;

– площадь живого сечения, м²;

– гидравлический радиус, м;

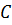- коэффициент Шези, м^0,5/с;

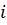- уклон дна.

Для определения нормальной глубины находим модуль расхода, которым должен характеризоваться канал в случае, если в русле установится равномерное движение .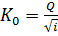

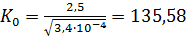м³/с.

Задаваясь произвольной величиной , определяем расходную характеристику 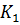при этой глубине. Если найденное значение 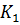отклоняется от не более чем на 5%, то глубину можно считать равной искомой глубине потока . Рассчитывается отклонение по формуле (1.2). В противном случае следует задаться новой глубиной и проверку модуля расхода . Для расчёта пользуемся графиком расходной характеристики 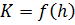, для построения которого подсчитываем расходные характеристики при нескольких глубинах. Расчёт ведём в табличной форме (таблица 1.1).

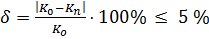(1.2)

Таблица 1.1 – К построению графика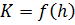

Величина или расчётная формула	Единица измерения	Численные значения
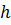
	м	1,00	1,2	1,1	1,05
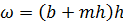
	м^2	3,40	4,37	3,87	3,63
	м	5,32	5,95	5,64	5,48
	м	0,64	0,73	0,69	0,66
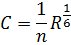
	м^0,5/с	44,21	45,19	44,76	44,43
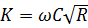
	м^3/с	120,25	168,73	143,89	131,02

По данным таблицы 1.1 строим график 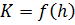(рисунок 1.1). Отложив на оси абсцисс точку, соответствующую расходной характеристике , по графику находим искомую глубину . Для проверки графического решения при найденной глубине найдем отклонение по формуле (1.2), которое не должно превышать 5 %, если все вычисления выполнены правильно.

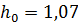м – по графику,

м²,

м,

м,

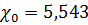м^0,5/с,

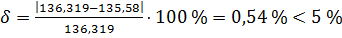
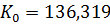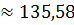м³/с м³/с.

Принимаем нормальную глубину потока 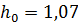м.

1. 2 Расчёт критической глубины

Критической глубиной (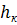) называется глубина, отвечающая минимуму удельной энергии сечения.

Определяем критическую глубину, используя уравнение критического состояния

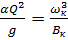, (1.3)

где и - соответственно площадь живого сечения и ширина потока поверху, отвечающие критической глубине .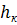

Величина является постоянной и её вычисляем по известному расходу 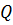, при .

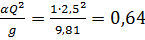м⁵.

Затем, задаваясь рядом значений 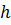, строим график (рисунок 1.2), по которому определяем 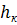, соответствующее известному значению .

Расчёт ведём в табличной форме (таблица 1.2).

Таблица 1.2 – К построению графика

Величина или расчётная формула	Единица измерения	Численные значения
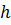
	м	0,50	0,25	0,40	0,45
	м	1,40	0,625	1,07	1,23
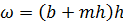
	м^2	3,40	2,80	3,16	3,28
	м^5	0,81	0,03	0,39	0,57

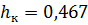м – по графику,

м,

м², Проверяем не превышает 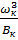более чем на 5 % велечину по формуле:

(1.4)

.

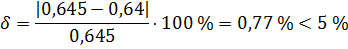
Принимаем критическую глубину 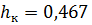м.

1. 3 Расчёт критического уклона

Критическая глубина зависит только от геометрической формы поперечного сечения русла и расхода, но не зависит от продольного уклона дна .

При равномерном движении жидкости нормальная глубина, как это следует из формулы (1.1), зависит именно от уклона. Тогда очевидно, для русла, при заданном расходе 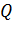, можно подобрать такое значение , при котором нормальная глубина 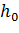станет равной критической 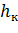, такой уклон обозначается через и называется критическим.

Таким образом критическим уклоном называется уклон, при котором нормальная глубина равна критической - .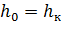

Для определения нужно решить совместно уравнения (1.1), принимая 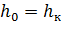, и (1.3), откуда

Нам известны:

м,

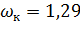м².

Вычисли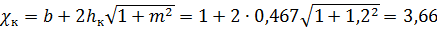м:

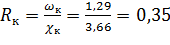м;

м;

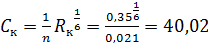м^0,5/с.

Теперь определим :

.

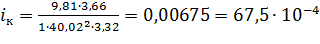Так как 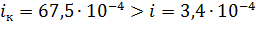, то и поток при равномерном движении будет находиться в спокойном состоянии.

Дата добавления: 2015-05-23