
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Подбор требуемого диаметра для одной нитки трубопровода
|
|
|
|
Дюкер (гидротехнический) - это заглубленная труба под рекой, каналом, другими сооружениями для пропуска заданного расхода воды. В курсовой работе с помощь дюкера соединяются два цилиндрических канала.
Гидравлический расчет дюкера состоит в подборе необходимого диаметра трубопровода для пропуска заданного расхода при известных характеристиках русла, дюкера, расхода и разности горизонтов воды в разных сечениях.
Для этого составим уравнение Бернулли для двух сечений относительно плоскости сравнения.
z1 + P1/ρg + αV12/ 2g = z3 + P3/ρg + αV32/ 2g + Σhf (2.1)
Z1=∆h=hн-hв , Z3=0, P1=P3=Pатм.
где hf – потеря напора на трение.
Преобразуя формулу, мы получим:
Δh + αV12/ 2g = αV32/ 2g + hL +hm;
где hm – местные потери, hm = (ζвход + 2ζповор. + ζреш)· V22/2g + (V2 –V3)2/2g
hL – потери по длине, hL = (λL2 ·V22)/d·2g.
Подставив данные выражения, мы получаем:
Δh = α(V32 - V12)/ 2g + (λL2 ·V22)/d·2g +(ζвход + 2ζповор. + ζреш)· V22/2g + (V2 –V3)2/2g;
ζповор = A·B = 2.5·0.05 = 0,125;
ζреш = 2,0
ζвход + 2ζповор. + ζреш = 0.50 + 2·0.125+2 = 2,75
Reпред. = 500/Δr;
Δr = Δ/d;
V3 = Q/w3 = 0.446(м/с)
V1 = Q/w1 = 0.272 (м/с)
α(V32 - V12)/ 2g = 1(0.4462 – 0.2722)/(2·9.81) = 0.00634
Таблица 2.1 – Определение диаметра трубопровода
| d | W2 | V2 | Re | Re пр2 | Область сопротивления | ƛ | hl | hм | ∆h |
| 1,4 | 1,539 | 1,625 | 2274795,268 | 712727,273 | квадратичная | 0,018 | 0,027 | 0,441 | 0,474 |
| 1,5 | 1,766 | 1,415 | 2123142,251 | 763636,364 | квадратичная | 0,018 | 0,018 | 0,354 | 0,354 |
| 1,6 | 2,01 | 1,244 | 1990445,86 | 814545,455 | квадртатичная | 0,017 | 0,013 | 0,249 | 0,269 |
| 1,7 | 2,269 | 1,102 | 1873360,809 | 865454,545 | квадратичная | 0,017 | 0,01 | 0,192 | 0,208 |
W2=(π*d2)/4
V2=Q/W
Re=V2*d/υ
υ =10-6
∆h= α·(v22-v32)/ 2·q + hm + λ·L·v2/d·2·q
По данным таблицы строим график V = f(d) и Δh = f(d).
Вывод: диаметр принимаем равным 1.56, а скорость 1.31 м/с. Такие параметры необходимы для пропуска расхода 1 м3/с и обеспечения разности уровней 0.3 м.
3 РАСЧЁТ КАНАЛА ПАРАБОЛИЧЕСКОГО СЕЧЕНИЯ
3. 1 Расчёт нормальной глубины потока
Глубина потока, соответствующая равномерному движению, называется нормальной глубиной и обозначается символом  . Основной зависимостью при определении нормальной глубины в данном расчёте является уравнение (1.1).
. Основной зависимостью при определении нормальной глубины в данном расчёте является уравнение (1.1).
Для определения нормальной глубины находим модуль расхода, которым должен характеризоваться канал в случае, если в русле установится равномерное движение 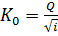 .
.
 м3/с.
м3/с.
Задаваясь произвольной величиной  , определяем расходную характеристику
, определяем расходную характеристику 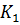 при этой глубине. Если найденное значение
при этой глубине. Если найденное значение 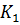 отклоняется от
отклоняется от  не более чем на 5%, то глубину
не более чем на 5%, то глубину  можно считать равной искомой глубине потока
можно считать равной искомой глубине потока  . В противном случае следует задаться новой глубиной
. В противном случае следует задаться новой глубиной  и проверку модуля расхода
и проверку модуля расхода  . Для расчёта пользуемся графиком расходной характеристики
. Для расчёта пользуемся графиком расходной характеристики 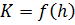 , для построения которого подсчитываем расходные характеристики при нескольких глубинах. Расчёт ведём в табличной форме (таблица 3.1).
, для построения которого подсчитываем расходные характеристики при нескольких глубинах. Расчёт ведём в табличной форме (таблица 3.1).
Таблица 3.1 – К построению графика 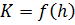
| Величина или расчётная формула | Единица измерения | Численные значения | |||
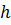
| м | 1,90 | 2,00 | 1,80 | 1,85 |
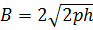
| м | 4,93 | 5,06 | 4,80 | 4,87 |
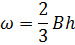
| м2 | 6,24 | 6,75 | 5,76 | 6,01 |

| - | 0,38 | 0,39 | 0,37 | 0,38 |
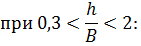
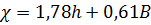 ;
при ;
при 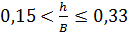 : :
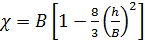 ; ;
| м | 6,39 | 6,65 | 6,13 | 6,26 |

| м | 0,98 | 1,01 | 0,94 | 0,96 |
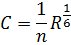
| м0,5/с | 38,33 | 38,52 | 38,07 | 38,20 |
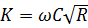
| м3/с | 236,77 | 261,31 | 212,60 | 224,94 |
По данным таблицы 3.1 строим график 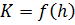 (рисунок 3.1). Отложив на оси абсцисс точку, соответствующую расходной характеристике
(рисунок 3.1). Отложив на оси абсцисс точку, соответствующую расходной характеристике  , по графику находим искомую глубину
, по графику находим искомую глубину  . Для проверки графического решения при найденной глубине
. Для проверки графического решения при найденной глубине  определяем отклонение по формуле (1.2), которое не должно превышать 5 %, если все вычисления выполнены правильно.
определяем отклонение по формуле (1.2), которое не должно превышать 5 %, если все вычисления выполнены правильно.
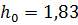 м – по графику,
м – по графику,
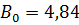 м,
м,
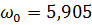 м2,
м2,
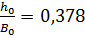
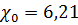 м,
м,
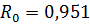 м,
м,
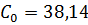 м0,5/с,
м0,5/с,

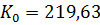 м3/с
м3/с
Принимаем нормальную глубину потока 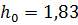 м.
м.
3. 2 Расчёт критической глубины
Критической глубиной (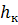 ) называется глубина, отвечающая минимуму удельной энергии сечения.
) называется глубина, отвечающая минимуму удельной энергии сечения.
Определяем критическую глубину, используя уравнение критического состояния (1.3).
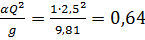 м5.
м5.
Затем, задаваясь рядом значений 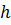 , строим график
, строим график  (рисунок 3.2), по которому определяем
(рисунок 3.2), по которому определяем 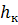 , соответствующее известному значению
, соответствующее известному значению  .
.
Расчёт ведём в табличной форме (таблица 3.2).
Таблица 3.2 – К построению графика 
| Величина или расчётная формула | Единица измерения | Численные значения | |||
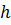
| м | 0,50 | 0,60 | 0,70 | 0,65 |
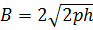
| м | 2,53 | 2,77 | 2,99 | 2,88 |
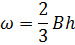
| м2 | 0,84 | 1,11 | 1,39 | 1,25 |

| м5 | 0,24 | 0,49 | 0,91 | 0,67 |
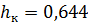 м – по графику,
м – по графику,
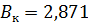 м,
м,
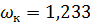 м2,
м2,
Проверяем не превышает 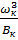 более чем на 5 % велечину
более чем на 5 % велечину  по формуле (1.4).
по формуле (1.4).
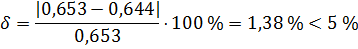
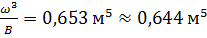 .
.
Принимаем критическую глубину 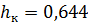 м.
м.
3. 3 Расчёт критического уклона
Критическая глубина зависит только от геометрической формы поперечного сечения русла и расхода, но не зависит от продольного уклона дна 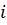 .
.
При равномерном движении жидкости нормальная глубина, как это следует из формулы (1.1), зависит именно от уклона. Тогда очевидно, для русла, при заданном расходе 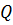 , можно подобрать такое значение
, можно подобрать такое значение 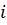 , при котором нормальная глубина
, при котором нормальная глубина  станет равной критической
станет равной критической 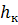 , такой уклон обозначается через
, такой уклон обозначается через 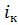 и называется критическим.
и называется критическим.
Таким образом критическим уклоном называется уклон, при котором нормальная глубина равна критической - 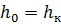 .
.
Для определения 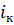 нужно решить совместно уравнения (1.1), принимая
нужно решить совместно уравнения (1.1), принимая 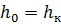 , и (1.3), откуда
, и (1.3), откуда

Нам известны:
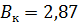 м,
м,
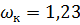 м2.
м2.
Вычислим:
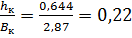 ;
;
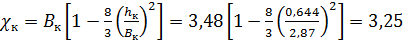 м;
м;
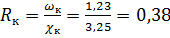 м;
м;
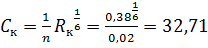 м0,5/с.
м0,5/с.
Теперь определим 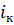 :
:
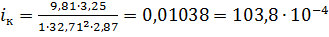 .
.
Так как 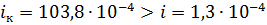 , то
, то 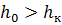 и поток при равномерном движении будет находиться в спокойном состоянии.
и поток при равномерном движении будет находиться в спокойном состоянии.
|
|
|
|
|
Дата добавления: 2015-05-23; Просмотров: 513; Нарушение авторских прав?; Мы поможем в написании вашей работы!