Практичне заняття №4 Планування експерименту з якісними факторами

Контрольні питання

1. У яких випадках використовується симплекс-гратчасте планування?

2. Як перевірити адекватність одержаної моделі?

3. Як визначається дисперсія?

4. Яким чином обчислюються коефіцієнти моделі?

5. Як визначається число мір свободи?

Мета заняття – ознайомитися з методами планування й аналізу експерименту з якісними чинниками.

Вихідні дані

Досліджується тривалість технічного обслуговування автомобілів механіками з різним виробничим стажем. Рівні чинника складають: перший – 6 років, другий – 12 років, третій – 18 років.

Для кожного з рівнів проведено по чотири рандомізованних виміри тривалості технічного обслуговування в годиннику, табл.4.1.

Таблиця 4.1

Параметри	Рівні фактора Х-стаж механіка
Перший-6 рок.	Другий-12 рок.	Третій-18 рок.
Продуктивність технічного обслуговування, год.
Номер заміру
Число вимірів на кожному з рівнів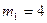
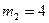
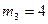
Середнє арифметичне тривалості обслуговування, год.
Дисперсія на кожному з рівнів чинників		8,66	3,33

Потрібно перевірити за рівні значущості Р=0,05 рівність середніх арифметичних тривалості обслуговування, тобто впливи стажу.

Порядок виконання роботи

1. Розраховуються середні арифметичні тривалості обслуговування (функції відгуку) на кожному з рівнів

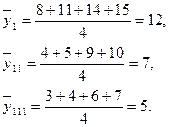
2. Розраховується загальне середнє арифметичне для всього експерименту

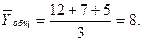
3. Розраховується дисперсія функції відгуку для кожного з рівнів чинників за формулою:

.

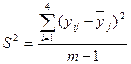Тоді для першого рівня

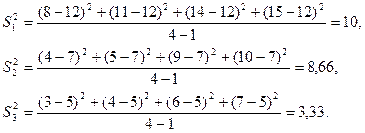
4. Перевіряється однорідність дисперсії за допомогою критерію Кохрена.

.

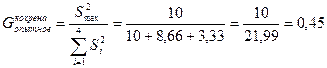5. За таблицями для Р=0,05 N=m=4 і числа ступенів свободи K=n-1=3-1=2 визначається табличне значення критерію Кохрена

,

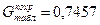Де n – число часних дисперсій.

6. Оцінюється однорідність дисперсії вимірів функції відгуку.

Виходячи з

,

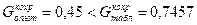то дисперсії однорідні.

7. Визначається загальна сума квадратів відхилень функції відгуку від загального середнього за формулою:

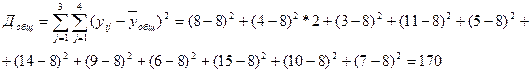
9. Визначається сума чинника квадратів відхилення

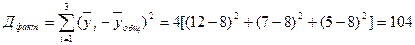
де 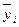– середнє арифметичне функції відгуку на кожному з рівнів.

10. Визначається залишкова сума квадратів

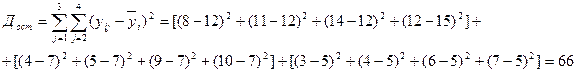
11. Загальна сума квадратів відхилень дорівнює сумі залишкової та сум факторів (за теорію).

170 =66+104= 170.

Отже, розрахунки виконані правильно.

12. Визначається загальна незміщена дисперсія

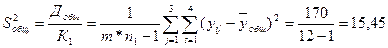
де 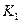– число ступенів свободи

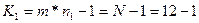
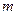– число замірів «у» для кожного рівня факторів;

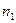– число рівнів факторів.

13. Визначається незміщена дисперсія чинника

.

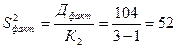
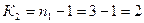13. Визначається незміщена залишкова дисперсія

.

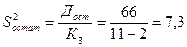
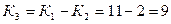14. Визначається опитне значення критерію Фішера

.

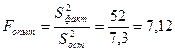15. Визначається табличне значення критерію Фішера для Р=0,05,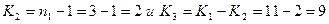

за таблицею

.

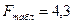16. Тоді

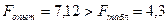, то

середні арифметичні обслуговування автомобілів механіками з різним стажем відрізняються одне від одного статистично значущо.

17. Строиться график связи

Дата добавления: 2015-05-23