Методические указания. Кинематика и динамика жидкостей

Кинематика и динамика жидкостей

Виды движения жидкости. Основные понятия кинематики жидкости: линия тока, трубка тока, струйка, живое сечение, расход. Поток жидкости. Средняя скорость. Уравнение расхода. Дифференциальные уравнения движения идеальной жидкости. Уравнение Бернулли для установившегося движения идеальной жидкости. Геометрическое и энергетическое толкование уравнения Бернулли. Уравнение Бернулли для относительного движения идеальной жидкости. Уравнение Бернулли для потока вязкой жидкости. Коэффициент Кориолиса. Общие сведения о гидравлических потерях. Виды гидравлических потерь. Трубка Пито. Расходомер Вентури. Краткие сведения о движении газов; условия применимости законов гидравлики к движению газов.

Основным уравнением гидродинамики является уравнение Бернулли. Его составляют для двух живых сечений потока, и для установившегося движения реальной жидкости имеет следующий вид:

, (8)

где – геометрический напор или высота положения – расстояние от произвольно выбранной горизонтальной плоскости сравнения до центра тяжести сечения (в энергетическом смысле – это удельная, т.е. отнесенная к единице веса жидкости, потенциальная энергия положения); р – давление в центре тяжести сечения; 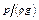– пьезометрический напор – вертикальное расстояние между центром тяжести сечения и уровнем жидкости в пьезометре (удельная потенциальная энергия давления); 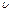– средняя скорость потока в сечении; a – коэффициент Кориолиса (отношение действительной кинетической энергии потока к условной кинетической энергии, вычисленной по средней скорости); 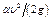– скоростной напор (удельная кинетическая энергия); 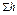– гидравлические потери напора (та часть удельной механической энергии, которую жидкость теряет на преодоление сопротивлений на участке потока между сечениями 1 и 2. Вследствие работы сил трения она превращается в тепловую энергию и рассеивается в пространстве). Гидравлические потери состоят из потерь на трение 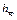и местных потерь h _м, т. е. 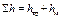. Уравнение Бернулли является частным случаем закона сохранения энергии. Оно может быть выражено и в другом виде, где все члены представляют собой энергию, отнесенную к единице объема:

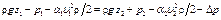, (9)

где 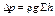– потери давления.

Как видно, уравнение Бернулли выражает связь между тремя разными величинами потока: высотой положения z, давлением р и средней скоростью .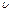

При решении практических задач вместе с уравнением Бернулли применяется и уравнение постоянства расхода, т. е. равенства расхода Q во всех сечениях установившегося потока:

. (10)

Из него следует, что средние скорости 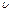обратно пропорциональны площадям S живых сечений.

При использовании уравнения Бернулли целесообразно руководствоваться следующим:

1) оно применяется только для установившегося движения вязкой несжимаемой жидкости в том случае, когда из массовых сил на нее действует лишь сила тяжести;

2) два живых сечения, к которым применяется уравнение Бернулли, должны быть нормальными к векторам скоростей и располагаться на прямолинейных участках потока. Движение жидкости в окрестности выбранных сечений должно быть параллельноструйным или плавно изменяющимся, хотя между ними поток может быть и резко изменяющимся. На участке потока между сечениями не должно быть источника или потребителя энергии жидкости (насоса или гидродвигателя);

3) если поток неустановившийся или на участке между расчетными сечениями имеется источник или потребитель энергии, к приведенным уравнениям (8,9) необходимо дописать дополнительные члены;

4) обычно расчетные сечения удобно подбирать там, где известно давление. Но в уравнение должна попасть и неизвестная величина, которую нужно определить. Нумерация выбранных сечений 1 и 2 производится по направлению потока. В противном же случае меняется знак гидравлических потерь 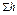или D р;

5) плоскость сравнения должна быть горизонтальной. По высоте ее можно подобрать произвольно, но очень часто удобно использовать плоскость, проходящую через центр тяжести нижнего расчетного сечения;

6) геометрический напор z выше плоскости сравнения считается положительным, а ниже – отрицательным;

7) когда площадь расчетного сечения сравнительно большая, скоростной напор 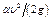и член являются ничтожными по сравнению с другими членами и приравниваются нулю.

Дата добавления: 2015-05-23