Методические указания. Турбулентное движение жидкости

Турбулентное движение жидкости

Особенности турбулентного движения жидкости. Пульсации скоростей и давлений. Распределение осредненных скоростей по сечению. Касательные напряжения в турбулентном потоке. Потери напора в трубах. Формула Дарси; коэффициент потерь на трения по длине (коэффициент Дарси). Шероховатость стенок, абсолютная и относительная. Графики Никурадзе и Мурина. Гидравлически гладкие и шероховатые трубы. Формулы для определения коэффициента Дарси и области их применения. Движение в некруглых трубах.

Потери напора на трение по длине трубы при турбулентном движении определяют также по формуле Дарси (11), но в этом случае коэффициент трения l, определяют по другим зависимостям, чем в ламинарном потоке. Таким образом, формула Дарси является универсальной – ее можно применять для любых жидкостей при любом режиме движения.

Имеется ряд формул для определения коэффициента l в зависимости от режима течения жидкости и числа Рейнольдса, например:

1) ламинарное движение (I зона, );

2) неопределенное движение (II зона, ). Трубопроводы с движением, соответствующим этой зоне, проектировать не рекомендуется;

3) турбулентное движение ():

а) зона гладких труб (III зона, ). Формула Прандтля – Никурадзе

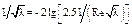. (13)

б) переходная зона (IV зона, 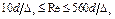), формула Колбрука:

. (14)

в) зона шероховатых труб (V зона, ), формула Прандтля-Никурадзе:

. (15)

Зону V еще называют зоной квадратичного сопротивления, так как здесь гидравлические потери на трение пропорциональны квадрату скорости. Для турбулентного движения самой общей является формула IV зоны. Из нее как частные случаи легко получаются формулы для III и V зон. С увеличением номера зоны растет число Рейнольдса, увеличивается турбулентность, толщина ламинарного пристенного слоя уменьшается и, следовательно, увеличивается влияние шероховатости и уменьшается влияние вязкости, т.е. числа Rе на коэффициент гидравлического трения. В первых трех зонах коэффициент зависит лишь от числа Rе, в IV зоне – от числа Rе и относительной шероховатости D_э/ d, а в V зоне – лишь от шероховатости D_э/ d.

Для труб промышленного изготовления с естественной шероховатостью для любой области сопротивления при турбулентном режиме движения можно пользоваться формулой А.Д. Альтшуля:

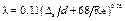. (16)

Пользоваться приведенными формулами для определения коэффициента l не всегда удобно. Для облегчения расчета здесь приводится номограмма Колбрука – Уайта (см. приложение 3), при помощи которой l определяется весьма просто по известным Rе и D_э/ d.

Дата добавления: 2015-05-23