
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгоритм знаходження оптимальних значень цільової функції графічним методом
|
|
|
|
Графічне розв’язування задачі лінійного програмування
Область визначення задачі лінійного програмування, яка визначається обмеженнями (5) та (6), являє собою випуклу многогранну множину. Кожна точка цієї множини називається планом задачі, а кожна вершина — опорним планом задачі.
Задача лінійного програмування має розв’язок, якщо існує вектор 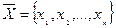 , що задовольняє умови (5) та (6), і приводить функцію (4) до екстремуму.
, що задовольняє умови (5) та (6), і приводить функцію (4) до екстремуму.
При 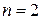 задача лінійного програмування має вигляд:
задача лінійного програмування має вигляд:
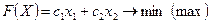 (8)
(8)
за умов 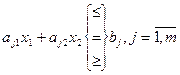 (9)
(9)
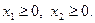 (10)
(10)
I. За обмеженнями (9) та (10) будуються граничні прямі:
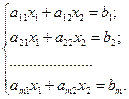
II. Кожному обмеженню (9) та (10) визначаємо відповідну йому півплощину за допомогою підстановки точки з даної півплощини: якщо нерівність виконується у даній точці, то півплощина, яка містить дану точку буде шуканою, якщо нерівність не виконується, то шуканою буде півплощина, яка дану точку не містить.
Таким чином знаходять многокутник розв’язків як перетин відповідних півплощин. Многокутник розв’язків — це область, кожна точка якої задовольняє систему обмежень (9) та (10).
ІІІ. Виберемо довільну сталу 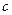 і матимемо рівняння
і матимемо рівняння 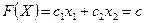 . Це рівняння визначає на площині сукупність паралельних прямих
. Це рівняння визначає на площині сукупність паралельних прямих  , які будуть перпендикулярними до вектора нормалі цільової функції
, які будуть перпендикулярними до вектора нормалі цільової функції 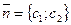 . Пряма
. Пряма  називається лінією рівня функції
називається лінією рівня функції 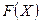 , яка відповідає значенню
, яка відповідає значенню 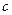 .
.
Будують вектор 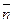 і лінію рівня
і лінію рівня 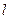 , яка перетинає область.
, яка перетинає область.
IV. Лінію рівня зміщують паралельно самій собі в напрямі вектора 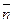 до тих пір, поки пряма
до тих пір, поки пряма 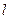 не досягне крайньої точки області, в якій цільова функція набуде максимального значення (це остання спільна точка з областю) або мінімального (перша спільна точка з областю).
не досягне крайньої точки області, в якій цільова функція набуде максимального значення (це остання спільна точка з областю) або мінімального (перша спільна точка з областю).
V. Визначають координати вершини екстремуму, як координати точки перетину відповідних прямих.
VI. Обчислюють значення цільової функції в отриманих точках і знаходять оптимальне значення цільової функції 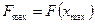 або
або 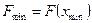 .
.
При графічному розв’язуванні задач лінійного програмування можуть зустрітися такі випадки:
— цільова функція набуває екстремального значення в одні точці (рис. 1);
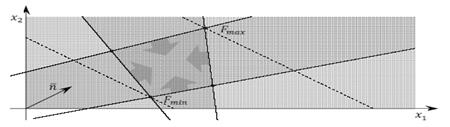
Рис. 1
— цільова функція набуває максимального чи мінімального значення в кожній точці відрізка, отже задача має безліч альтернативних планів: 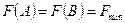 (рис. 2);
(рис. 2);
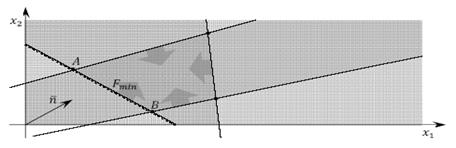
Рис. 2
— цільова функція F(Х) необмежена зверху в необмеженій області: 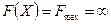 (рис. 3);
(рис. 3);
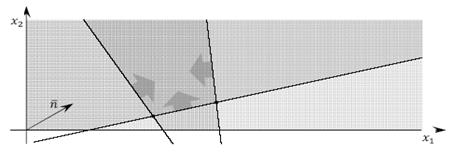
Рис. 3
— допустима область складається з однієї точки: 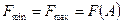 (рис. 4);
(рис. 4);
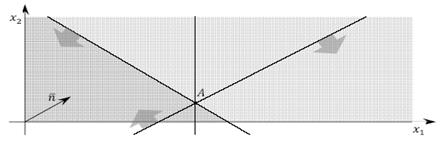
Рис. 4
— цільова функція розв’язку не має, оскільки система обмежень (9), (10) є несумісною (рис. 5).
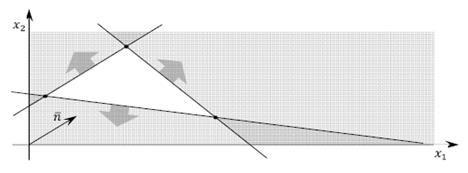
Рис. 5
Приклад 2. Розв’язати графічно задачу лінійного програмування:
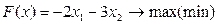

Розв’язання: І.За обмеженнями системи будуємо граничні прямі через дві точки (рис. 6).
Для прямої 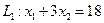 при
при 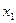 =0,
=0, 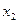 =6; при
=6; при 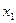 =3,
=3, 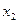 =5.
=5.
Для прямої 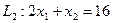 при
при 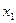 =8,
=8, 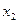 =0; при
=0; при 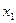 =5,
=5, 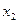 =6.
=6.
Пряма 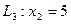 проходить паралельно осі
проходить паралельно осі 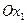 .
.
Пряма 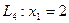 проходить паралельно осі
проходить паралельно осі 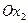 .
.
Для прямої 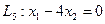 ; при
; при 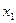 =0,
=0, 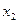 =0;при
=0;при 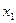 =4,
=4, 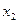 =1.
=1.
II. Кожному обмеженню системи визначимо відповідну півплощину за допомогою підстановки точки з даної півплощини. Многокутником розв’язків є многокутник АВСD.
III. Будуємо вектор 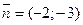 і лінії рівня
і лінії рівня 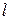 , які перетинають область.
, які перетинають область.
IV. Лінії рівня та многокутник розв’язків мають першу спільну точку –точку С, тобто в цій точці цільова функція має мінімум, а остання спільна точка-це точка А, в цій точці цільова функція має максимум.
V. Визначимо координати точки А як кооординати точки перетину осі 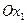 та прямой
та прямой 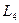 :
: 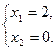 Таким чином, точка А має координати
Таким чином, точка А має координати 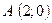 .
.
Визначимо координати точки С як кооординати точки перетину прямих 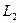 та
та 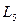 :
: 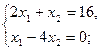
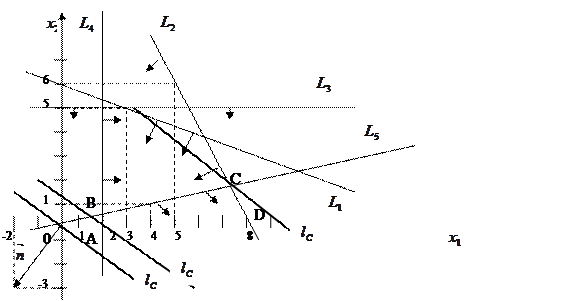
Рис. 6
Визначимо координати точки А як кооординати точки перетину осі 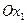 та прямой
та прямой 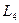 :
: 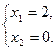 Таким чином, точка А має координати
Таким чином, точка А має координати 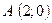 .
.
Визначимо координати точки С як кооординати точки перетину прямих 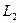 та
та 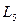 :
: 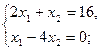
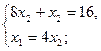
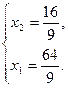 Таким чином, точка С має координати
Таким чином, точка С має координати 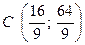 .
.
VI. Визначаємо значення цільової функції в отриманих точках:
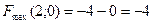 ,
, 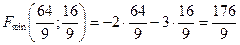 Відповідь:
Відповідь: 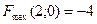 ;
; 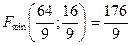 .
.
Теорія двоїстості в лінійному програмуванні
Кожній задачі лінійного програмування можна поставити у відповідність іншу, спеціально побудовану задачу, яка називається двоїстою до даної. Дві такі задачі утворюють пару взаємнодвоїстих задач. Початкову задачу в такій парі називають прямою або вихідною. Якщо прямою вважати двоїсту задачу, то двоїста до неї буде збігатися з початковою.
Побудуємо пару двоїстих задач.
Нехай задано задачу
лінійного програмування:
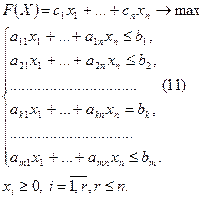
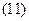 яку вважатимемо прямою
задачею.
яку вважатимемо прямою
задачею.
| Двоїстою до неї буде така задача:
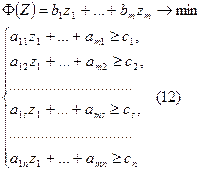 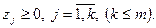
|
Правила побудови двоїстої задачі:
1. Одна із задач двоїстої пари повинна бути на знаходження найбільшого, а інша — на знаходження найменшого значення цільової функції.
2. Обмеження в задачі на максимум повинні бути записані за допомогою 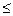 і (або) =, а в задачі на мінімум — за допомогою
і (або) =, а в задачі на мінімум — за допомогою 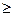 і (або) =.
і (або) =.
3. Кількість змінних однієї задачі має бути такою самою, як кількість нерівностей і рівнянь в системі обмежень іншої задачі.
4. Кожній нерівності системи обмежень однієї задачі повинна відповідати в іншій задачі невід’ємна змінна, а кожному рівнянню повинна відповідати змінна в іншій задачі, на знак якої не накладено обмежень.
5. Коефіцієнти цільової функції однієї задачі повинні бути правими частинами (вільними членами) системи обмежень іншої задачі.
6. Матриця системи обмежень однієї задачі повинна бути транспонованою матрицею системи обмежень іншої задачі.
Приклад 3. Скласти двоїсту задачу до задачі лінійного програмування 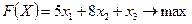
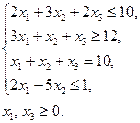
Розв’язання: Оскільки цільова функція прямує до максимуму, то всі знаки в системі обмежень мають бути 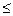 або
або 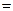 :
:
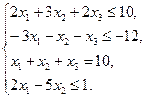
Кількість змінних двоїстої задачі дорівнює кількості обмежень прямої задачі за правилом 3, тобто в двоїстій задачі буду чотири змінних 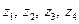 . Цільова функція двоїстої задачі повинна прямувати до мінімуму за правилом 1, за правилом 5 коефіцієнтами цільової функції є праві частини системи обмежень прямої задачі, таким чином маємо цільову функцію:
. Цільова функція двоїстої задачі повинна прямувати до мінімуму за правилом 1, за правилом 5 коефіцієнтами цільової функції є праві частини системи обмежень прямої задачі, таким чином маємо цільову функцію: 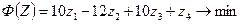 . Складемо матрицю системи обмежень прямої задачі і за правилом 6 її транспонуємо:
. Складемо матрицю системи обмежень прямої задачі і за правилом 6 її транспонуємо:
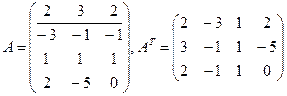 .
.
Таким чином, враховуючи, що за правилом 2 в системі обмежень знаки повинні бути 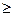 і (або) =. В системі обмежень двоїстої задачі друге обмеження буде рівністю за правилом 4, оскільки на другу змінну не було накладено умову невід’ємності:
і (або) =. В системі обмежень двоїстої задачі друге обмеження буде рівністю за правилом 4, оскільки на другу змінну не було накладено умову невід’ємності:
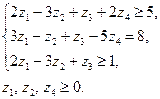
Розглянемо економічну інтерпретацію пари двоїстих задач.
Якщо пряму задачу можна трактувати як задачу планування виробництва продукції, то двоїсту до неї – як задачу знаходження об'єктивно зумовлених (граничних, маргінальних, двоїстих, тіньових) оцінок ресурсів, які б дали змогу порівнювати результати з витратами при різних планах виробництва продукції.
Між прямою та двоїстою задачами лінійного програмування існує тісний взаємозв’язок, який випливає із наступних теорем.
Теорема (основна нерівність теорії двоїстості). Для будь-яких допустимих розв’язків прямої задачі 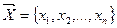 і двоїстої
і двоїстої 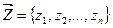 , справедлива нерівність:
, справедлива нерівність: 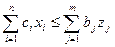 .
.
Теорема. Якщо 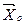 і
і 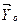 — допустимі плани взаємно двоїстих задач і значення цільових функцій
— допустимі плани взаємно двоїстих задач і значення цільових функцій 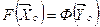 , то
, то 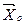 і
і 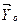 — оптимальні плани цих задач.
— оптимальні плани цих задач.
Теорема (мала теорема двоїстості). Для існування оптимального розв’язку кожної із задач двоїстої пари необхідно і достатньо існування допустимого розв’язку кожної з цих задач.
Теорема (основна теорема двоїстості). Якщо одна з задач двоїстої пари має оптимальний розв’язок, то і друга задача його має, при чому екстремальні значення цільових функцій збігаються. Якщо ж цільова функція однієї з задач необмежена, то друга задача допустимого розв’язку не має.
Економічне значення оптимального для двох задач розв’язку: сума виручки від продажу готових виробів дорівнює сумі виручки від продажу ресурсів. Якщо цільова функція прямої задачі не обмежена, то не знайдеться таких цін, які б скомпенсували це нескінченне значення цільової функції.
|
|
|
|
|
Дата добавления: 2015-05-23; Просмотров: 2546; Нарушение авторских прав?; Мы поможем в написании вашей работы!