Економічна постановка задачі, її математична модель

Двоїстий симплекс-метод

Суть двоїстого симплекс-методу полягає в тому, що для розв’язку пари двоїстих задач досить розв’язати одну із них.

Якщо розв’язана пряма задача має оптимальний розв’язок, то оптимальне значення змінних прямої задачі знаходимо в стовпчику вільних членів, а оптимальне значення змінних двоїстої задачі знаходимо в рядочку оцінок в оптимальному плані прямої задачі, враховуючи відповідності: .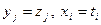

Транспортна задача лінійного програмування

Серед задач лінійного програмування можна виділити деякі види задач, моделі яких мають певну специфіку. Прикладом такої задачі є, так звана, транс­портна задача.

Постановка транспортної задачі пов'язана з визначенням такого плану пере­везення вантажу від постачальників до споживачів, при якому загальні транспортні витрати були б найменшими за умови, що мають бути задоволені потреби спожи­вачів. Можливості кожного постачальника, а також потреби кожного споживача вважаються відомими.

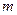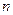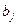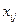Для побудови економіко-математичної моделі транспортної задачі введемо позначення: – кількість постачальників; – номер постачальника, ; – кількість вантажу в -го постачальника, ; – кількість споживачів; – номер споживача, ; – потреби -го споживача, ; – вартість перевезення одиниці вантажу від -го постачальника до -го споживача, , . Змінні моделі означають кількість вантажу, який перевозиться від -го постачальника до -го споживача. Тоді умову задачі можна записати у вигляді наступної таблиці (матриці планування):

Постачальники	Споживачі	Запаси
		…
					…
					…
…	…	…	…	…	…
					…
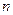
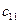
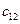
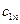
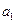
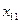
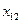
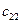
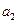
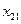
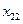
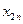
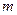
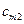
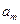
Потреби			…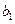

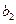
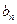
Загальні транспортні витрати 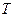обчислюються за формулою:

.

Згідно з критерієм оптимальності ці витрати мають бути мінімальними, тому цільова функція транспортної задачі прямує до мінімуму:

(13)

План перевезень 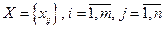має задовольняти умови:

– загальний обсяг вантажу, який вивозиться від кожного постачальника, повинен бути рівним його запасу:

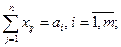(14)

– обсяг вантажу, який надходить кожному споживачеві, повинен бути рівним його потребам:

(15)

– обсяги вантажу на кожному з маршрутів мають бути невід'ємними:

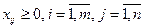. (16)

Система умов (13) – (16) є математичною моделлю транспортної задачі.

Якщо в транспортній задачі кількість продукції усіх постачальників рівна загальному попиту всіх споживачів, тобто

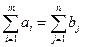, (17)

то таку транспортну задачу називають збалансованою або закритою. Якщо ж така умова не виконується, то ТЗ називається незбалансованою або відкритою.

Теорема. Будь-яка збалансована транспортна задача має розв’язок.

Для того, щоб розв’язати незбалансовану транспортну задачу спочатку необхідно її збалансувати. Можливі два випадки:

1. Загальні потреби споживачів більші від загального запасу продукції постачальників: .

У такому разі ТЗ нерозв’язна через наявність дефіциту продукції. Для розв’язування такої задачі необхідно ввести фіктивного постачальника, який забезпечить 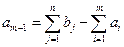одиниць продукції. Фіктивні поставки продукції означають дефіцит продукції у -го споживача.

2. Загальна кількість продукції постачальників більша від загального попиту споживачів: .

Для розв’язування такої задачі необхідно ввести фіктивного споживача.

Фіктивні поставки продукції 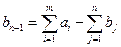означають залишок продукції у -го постачальника.

І в першій, і в другій ситуації норми витрат на доставку продукції рівні нулю.

Математична модель транспортної задачі (13)–(16) є задачею лінійного програмування. Специфіка цієї задачі полягає у системі її обмежень, яка є системою з 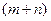лінійних рівнянь відносно змінних 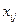. Виявляється, що дана система складається з 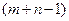лінійно незалежних рівнянь. Тому опорному розв’язку відповідатиме 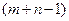лінійно незалежних векторів та кількість базисних маршрутів 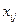для будь-якої транспортної задачі дорівнює .

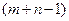Опорний план транспортної задачі називається невиродженим, якщо у ньому точно 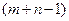додатних компонент .

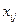Для розв’язування ТЗ можна використовувати симплекс-метод, проте зважаючи на специфіку ТЗ, можна застосовувати більш ефективний алгоритм – метод потенціалів.

Алгоритм методу потенціалів складається з таких етапів:

1. Визначення типу ТЗ (збалансована чи незбалансована). У другому випадку – збалансувати.

2. Побудова першого опорного плану ТЗ.

3. Визначення потенціалів опорного плану ТЗ.

4. Перевірка опорного плану ТЗ на оптимальність. Якщо умова оптимальності не виконується, то повторити дії, починаючи з п.3.

1. Як збалансувати ТЗ було розглянуто раніше. Переходимо до п.2.

2. Для побудови початкового опорного плану транспортної задачі існує кілька методів: північно-західного кута; мінімальної вартості; подвійної переваги, метод Фогеля та інші. Побудову опорного плану зручно подавати у вигляді таблиці, в якій постачальники продукції визначаються рядками, а споживачі - стовпчиками.

Дата добавления: 2015-05-23