
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Інтервальний варіаційний ряд
|
|
|
|
Якщо досліджувана ознака розподілена неперервно, то область зміни її значень розбивають на кілька однакових проміжків, які називають класами. Ширину класу визначають за формулою
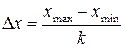 , (ІІІ.2)
, (ІІІ.2)
де k — кількість класів. Кількість класів та їх межі вибираються так, щоб межі класів були зручними для розрахунків. Оптимальною для вибірки об’ємом 80 – 150 елементів є кількість 8 – 12 класів.
Класи  разом з частотами пі попадання значень у кожен клас утворюють інтервальний варіаційний ряд.
разом з частотами пі попадання значень у кожен клас утворюють інтервальний варіаційний ряд.
Гістограмою відносних частот називають функцію, яка на кожному інтервалі  набуває значення
набуває значення 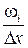 , де
, де  — відносна частота попадання значень змінної в цей інтервал. Площа підграфіка цієї функції на кожному проміжку
— відносна частота попадання значень змінної в цей інтервал. Площа підграфіка цієї функції на кожному проміжку  дорівнює відносній частоті попадання значень досліджуваної ознаки у цей проміжок, а площа всього підграфіка функції дорівнює одиниці. Тому гістограма відносних частот є емпіричною щільністю розподілу
дорівнює відносній частоті попадання значень досліджуваної ознаки у цей проміжок, а площа всього підграфіка функції дорівнює одиниці. Тому гістограма відносних частот є емпіричною щільністю розподілу  ознаки. Для побудови емпіричної функції розподілу
ознаки. Для побудови емпіричної функції розподілу 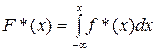 достатньо сполучити відрізками точки з координатами
достатньо сполучити відрізками точки з координатами  (тут
(тут 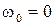 , а
, а  — відносна частота, що відповідає інтервалу
— відносна частота, що відповідає інтервалу 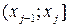 ).
).
Приклад 16. Час (у секундах) затрачений кожним із 124 учнів VII класу на розв'язування задачі з фізики становить:
| 14,7 | ||||||||||||||
| 17,5 | ||||||||||||||
| 30,5 | 49,2 | 54,4 | 24,6 | |||||||||||
| 33,3 | 51,5 | 49,2 | 42,4 | 54,4 | 53,5 | 32,8 | ||||||||
| 44,5 | ||||||||||||||
| 40,8 | ||||||||||||||
| 53,8 | 40,8 |
Побудувати інтервальний варіаційний ряд, гістограму відносних частот та емпіричну функцію розподілу даного часу. Знайти медіану та квартилі розподілу.
Розв’язання: Об’єм вибірки дорівнює 124. Внісши дані в пакет MS Excel та використавши стандартні функції НАИБОЛЬШИЙ та НАИМЕНЬШИЙ визначаємо, що 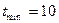 , а
, а  . Для зручності обчислень проміжок від 5 до 200 розіб’ємо на 15 інтервалів довжиною 13 кожен. Порахуємо частоти попадання значень випадкової величини Т в кожен з інтервалів (в Excel можна використати функцію СЧЁТЕСЛИ).
. Для зручності обчислень проміжок від 5 до 200 розіб’ємо на 15 інтервалів довжиною 13 кожен. Порахуємо частоти попадання значень випадкової величини Т в кожен з інтервалів (в Excel можна використати функцію СЧЁТЕСЛИ).
| (5;18] | (18;31] | (31;44] | (44;57] | (57;70] | (70;83] | (83;96] | (96;109] | (109;122] | (122;135] | (135;148] | (148;161] | (161;174] | (174;187] | (187;200] | |
| пі |
Інтервальний варіаційний ряд матиме вигляд:
| (5;18] | (18;31] | (31;44] | (44;57] | (57;70] | (70;83] | (83;96] | (96;109] | (109;122] | (122;135] | (135;148] | (148;161] | (161;174] | (174;187] | (187;200] | |
| wі | 0,032 | 0,226 | 0,202 | 0,226 | 0,105 | 0,056 | 0,056 | 0,032 | 0,008 | 0,024 | 0,016 | 0,008 | 0,000 | 0,000 | 0,008 |
Для побудови графіка емпіричної функції розподілу складаємо таблицю нагромаджених відносних частот

| ||||||||||||||||
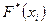
| 0,032 | 0,258 | 0,46 | 0,685 | 0,79 | 0,847 | 0,903 | 0,935 | 0,944 | 0,968 | 0,984 | 0,992 | 0,992 | 0,992 |
 |
Гістограма відносних частот та емпірична функція розподілу зображені на рис. 12.
Як видно з графіка, медіана  потрапляє на інтервал
потрапляє на інтервал 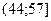 . Оскільки ми вважаємо розподіл значень у середині кожного інтервалу рівномірним, то для знаходження медіани скористаємось рівністю
. Оскільки ми вважаємо розподіл значень у середині кожного інтервалу рівномірним, то для знаходження медіани скористаємось рівністю 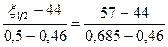 , звідки
, звідки 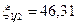 . Аналогічно для знаходження квартилей маємо
. Аналогічно для знаходження квартилей маємо  ,
, 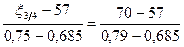 . Тоді
. Тоді  , а
, а  .
.
|
|
|
|
|
Дата добавления: 2015-05-23; Просмотров: 2597; Нарушение авторских прав?; Мы поможем в написании вашей работы!