Перевірка гіпотези про однорідність вибірки

Перевірка вибірки на однорідність має бути першим етапом статистичної обробки даних. Під однорідністю розуміють наявність в усіх елементів сукупності таких властивостей, які визначають їх однотипність. Неоднорідність вибірки може бути зумовлена наявністю похибки вимірювань даних або ж присутністю у вибірці аномальних елементів. Якщо неоднорідність вибірки зумовлена похибкою вимірювань і дослідник знає її причину, то відповідні елементи вибірки можна виключити перед початком статистичного аналізу даних. В іншому випадку потребують досліджень причини появи таких аномальних даних.

Задача перевірки вибірки на однорідність зводиться до перевірки таких гіпотез:

Н ₀: вибірка однорідна;

Н ₁: вибірка містить аномальні елементи (промахи).

Для перевірки цих гіпотез на заданому рівні значущості α використовують критерії Діксона.

Якщо елементи вибірки розміщені у порядку зростання 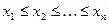, то перевірці на промах піддаються крайні ліві і крайні праві елементи. Формули для обчислення емпіричних значень критеріїв залежно від об’єму вибірки наведено у таблиці

Об’єм вибірки	Перевірка на промах х 1	Перевірка на промах хп
3≤ п ≤7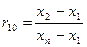
8≤ п ≤10
11≤ п ≤13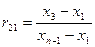
14≤ п ≤25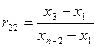

Критичні значення критеріїв Діксона наведені у таблиці 3 додатка.

Нульова гіпотеза приймається, якщо емпіричне значення критерію не перевищує критичного для 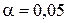, і відхиляємо, коли емпіричне значення критерію більше, ніж критичне для .

Приклад 19. Нехай при вимірюванні рівня вербального інтелекту за методикою Д.Век­слера у 12 студентів отримано наступні дані: 126, 127, 132, 120, 119, 126, 120, 123, 120, 116, 123, 115. Перевірити гіпотезу про однорідність отриманої вибірки.

Розв’язання: Впорядкувавши отримані дані, отримаємо такий варіаційний ряд:

115, 116, 119, 120, 120, 120, 123, 123, 126, 126, 127, 132.

Обчислимо значення 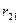для лівого краю ряду . Для правого краю . Критичні значення критерію , .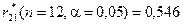

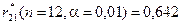Оскільки обидва емпіричні значення критерію не перевищують критичного для 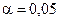, то приймається нульова гіпотеза, яка стверджує, що вибірка є однорідною.

Дата добавления: 2015-05-23