II. Основные теоретические положения

I. Цель работы

ИЗУЧЕНИЕ ПОТЕРЬ НАПОРА ПО ДЛИНЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ЖИДКОСТИ ПО ТРУБЕ

Установление области гидравлического сопротивления при движении жидкости в трубе. Определение опытных зна­чений коэффициента гидравлического трения и сопоставле­ние их с расчетными значениями.

При движении жидкости в трубе часть ее механической энергии вследствие трения обращается во внутреннюю (теп­ловую) энергию, которая не может быть снова обращена в механическую и поэтому рассматривается как потерянная. Эта потерянная энергия, отнесенная к единице веса жидко­сти, называется потерей напора по длине. Вели­чина потери напора по длине зависит от средней скорости течения, от длины трубы и ее сечения, от шероховатости поверхности и вязкости жидкости.

При равномерном движении жидкости в трубе круглого сечения потери напора по длине 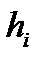рассчитываются по фор­муле Вейсбаха — Дарси

, (8)

где d и l — диаметр и длина трубы;

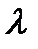- коэффициент гидравлического трения;

v - средняя скорость течения в трубе.

Коэффициент гидравлического трения 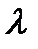в общем случае зависит от относительной шероховатости трубы 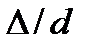( — эквивалентная шероховатость) и от числа Рейнольдса Re:

. (9)

При ламинарном движении зависимость (9) представ­ляется формулой Стокса, полученной теоретическим путем:

. (10)

Нетрудно убедиться, что в этом случае по зависимости (8) величина h _i является линейной функцией скорости v.

При турбулентном течении зависимость h_i от v перестает быть линейной. При этом различают три области гидрав­лического сопротивления:

1) область сопротивления гидравлически гладкой стенки. В этой области потери напора пропорциональны скорости в степени 1,75.

Коэффициент гидравлического трения определяется по закону Блазиуса

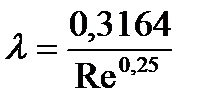; (11)

2) доквадратичная область сопротивления. В этой обла­сти потери напора пропорциональны скорости в степени, из­меняющейся в пределах от 1,75 до 2.

Коэффициент гидравлического трения определяется по обобщенному закону Колбрука

(12)

3) квадратичная область сопротивления. В этой области потери напора пропорциональны квадрату скорости.

Коэффициент гидравлического трения не зависит от числа Рейнольдса и определяется по формуле Прандтля — Никурадзе

. (13)

Наглядное представление о характере зависимости ко­эффициента от Re и /d дает график, представленный на рис. 5. На графике указаны два предельных числа Рей­нольдса (Re)’ _пред 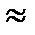10/ /d и (Re)"_пред 560/ /d, по которым проходят границы указанных областей гидравлического со­противления. Для области сопротивления гидравлически гладкой стенки указана другая зависимость коэффициента .

Следует отметить, что приведенные зависимости (10), (11), (12) и (13) справедливы для равномерного движения, которое наступает на расстоянии l_n >15 d от входа в трубу. На протяжении начального участка потери напора больше, нем в равномерном потоке.

В настоящей работе потери напора по длине изучаются на участке равномерного движения жидкости в трубе круг­лого сечения.

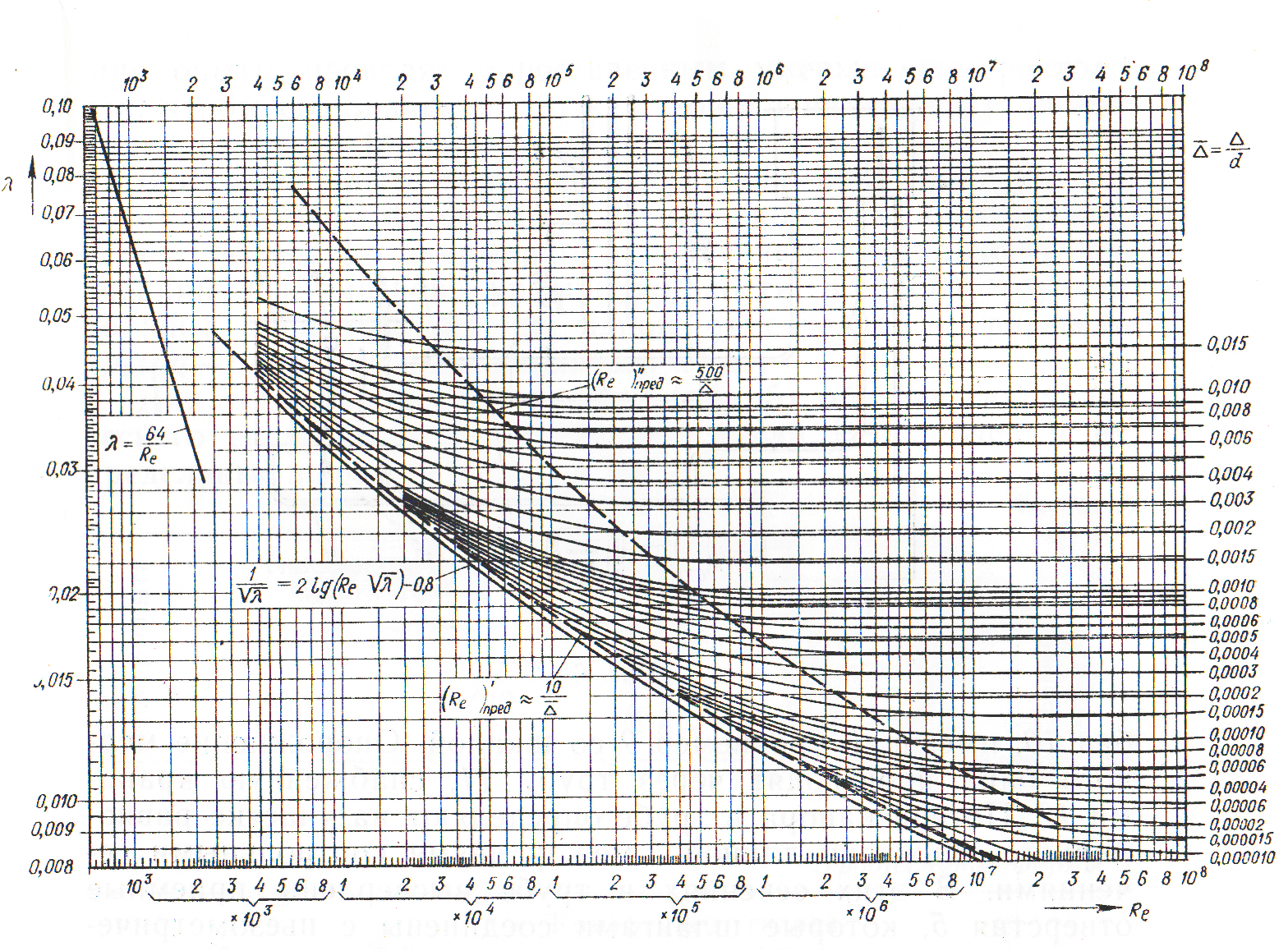
Рис. 3. Зависимость коэффициента от числа Re и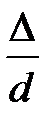

Дата добавления: 2015-05-23