II. Основные теоретические положения. Построение по данным измерений пьезометрической и гидродинамической линий диаграммы уравнения Бернулли для потока жидкости в трубопроводе

Лабораторная работа №1

ИЗУЧЕНИЕ ДИАГРАММЫ УРАВНЕНИЯ БЕРНУЛЛИ И МЕСТНЫХ ПОТЕРЬ НАПОРА

ПРИ УСТАНОВИВШЕМСЯ ДВИЖЕНИИ ЖИДКОСТИ

В ТРУБОПРОВОДЕ

I. Цель работы

Построение по данным измерений пьезометрической и гидродинамической линий диаграммы уравнения Бернулли для потока жидкости в трубопроводе. Определение опытных величин местных потерь напора и коэффициентов местных сопротивлений и сопоставление их с расчетными значениями.

Диаграмма уравнения Бернулли представляет собой его геометрическую интерпретацию (разъяснение), которая в гра­фическом виде отображает изменение удельной энергии по­тока (энергии, отнесенной к единице веса). Диаграмма (рис. 1) состоит из пьезометрической линии Р — Р, отображающей изменение удельной потенциальной энергии, и гидродинамической линии Е — Е, отображающей изменение удельной механической (т. е. потенциальной плюс кинетической) энергии.

Для двух любых контрольных сечений потока i — i и j—j (см. рис. 1) реальной жидкости при установившемся движе­нии уравнение Бернулли записывается в виде:

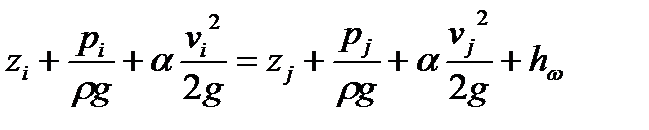, (1)

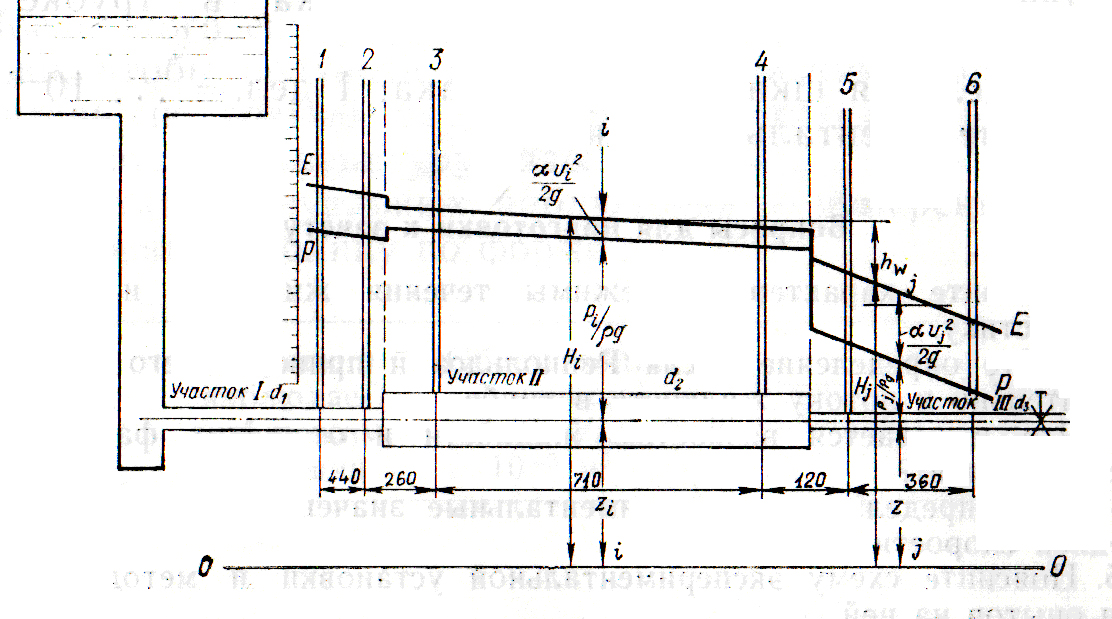Рис.1. Геометрическая интерпретация уравнения Бернулли

где 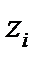и — геометрические высоты сечений по отноше­нию к горизонтальной плоскости сравнения 0 — 0 (если ось трубопровода горизонтальна, то z — const для всех сечени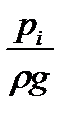й);

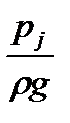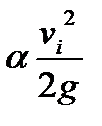и - пьезометрические высоты, соответствующие давлениям и

и 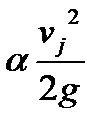- скоростные напоры, вычисленные по сред­ним скоростям течени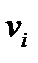й и ;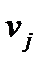

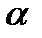- коэффициент (корректив) кинетической энер­гии;

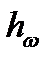— потеря удельной энергии или потеря напора на участке потока между контрольными сечениями.

Пьезометрическая линия расположена от плоскости сравнения 0 — 0 на расстоянии z+p/g ; гидродинамическая линия расположена от плоскости 0 — 0 на расстоянии H = z+p/g 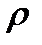+ (v²/2g). Величина Н называется гидроди­намическим напором. Согласно уравнению (1), по­теря напора — есть разность гидродинамических напоров в кон­трольных сечениях потока — 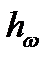=H_i — H_j .

Из уравнения (1) следует, что гидродинамическая линия имеет уклон вдоль потока, который называется гидроди­намическим уклоном. На участке равномерного движения гидродинамический уклон является постоянным. Соответственно уклон пьезометрической линии называется пьезометрическим уклоном.

На участках местной деформации потока пьезометриче­ская и гидродинамическая линии условно изображаются вертикальным уступом. Высота уступа гидродинамической линии графически изображает местную потерю напора h_M, т. е. ту часть энергии, которая вследствие местных, локаль­ных сил трения обращается во внутреннюю (тепловую) энер­гию, и поэтому считается потерянной. Местные потери на­пора рассчитываются по формуле Вейсбаха

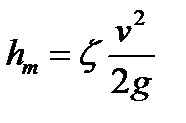, (2)

где 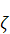— коэффициент местного сопротивления;

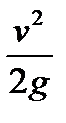— скоростной напор, определяемый по средней ско­рости 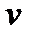в трубопроводе.

Величина коэффициента 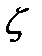зависит от вида местного сопротивления (сужения, расширения, поворота потока в трубе, в трубопроводной арматуре и т. д.). Для данного вида мест­ного сопротивления величина 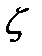при ламинарном и переход­ном режимах движения жидкости зависит также и от вяз­кости жидкости (точнее, от числа Рейнольдса Re). Число­вые значения коэффициентов 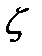приводятся в справочных руководствах по гидравлике.

Для случая резкого расширения потока в трубе (рис. 1) при определении местной потери напора по формуле (2) ко­эффициент 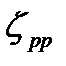принимают

, (3)

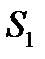где и 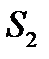— площади сечения потока в трубе на участках I и II (рис. 1).

Для случая резкого сужения потока в трубе (рис. 1) при определении местной потери напора по формуле (2) коэф­фициент 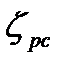принимают

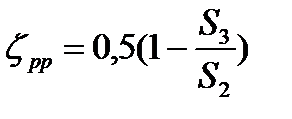, (4)

где 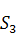— площадь сечения потока в трубе на участке III.

В настоящей работе рассматривается движение жидкости в горизонтальном трубопроводе, составленном из трех труб разного диаметра.

III. Описание лабораторной установки

На рис. 2 дана схема установки, на которой проводятся опыты по определению местных потерь напора и величин для построения диаграммы Бернулли. Трубопровод 1 с го­ризонтальной осью состоит из трех участков труб раз­личного диаметра с местными сопротивлениями. Подача жидкости в трубопровод производится из напорного бака 6. Напорный бак заполняется жидкостью с помощью насоса 2 из приемного бака 3 по трубопроводу 4, на котором уста­новлен вентиль 5. Уровень в баке в процессе опытов под­держивается на постоянной отметке благодаря частичному сливу жидкости через стенку. Расход жидкости в трубопро­воде регулируется вентилем 10. Истечение жидкости из трубопровода происходит в мерный бак 11, имеющий уровне­мер 12. Опорожнение мерного бака производится через трубу 14, снабженную кранами 13. В контрольных сечениях трубопровода высверлены приемные отверстия 7, которые с помощью шлангов соединены с пьезометрическими труб­ками 8. Трубки собраны на щите и имеют шкалу отсчетов 9.

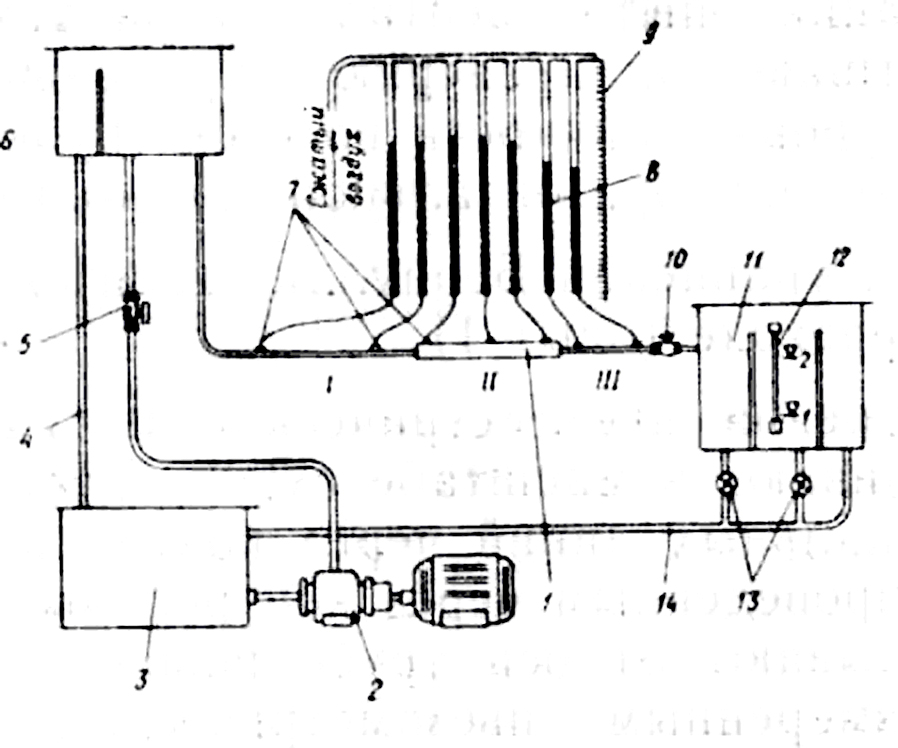Рис. 2. Схема лабораторной установки для определения местных потерь напора

Дата добавления: 2015-05-23