Уравнение Бернулли для идеальной жидкости

Коэффициент потерь на трение.

Коэффициент гидравлического сопротивления, который определяется в зависимости от числа Рейнольдса Re и от эквивалентной абсолютной шероховатости Δ_э. Для удобства сводные данные по определению λ представлены в таблице 4.1.

Пользоваться приведенными в табл. 4.1 формулами для определения коэффициента λ не всегда удобно. Для облегчения расчетов можно воспользоваться номограммой Колбрука-Уайта (рис.4.8), при помощи которой по известным Re и Δ_э/ d весьма просто определяется λ.

Является основным уравнением гидродинамики, оно устанавливает связь между скоростью потока жидкости и установившемся движением. Получим уравнение связанное между собой давление и скорость ее движения.

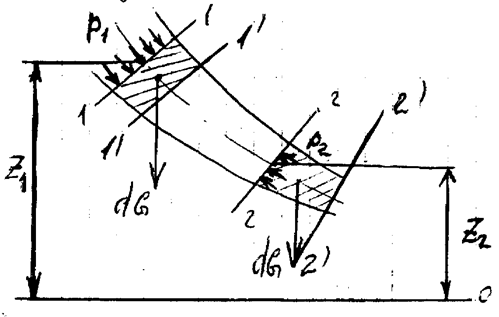Возьмем одну из элементарных струй составляю-щую объем и выделим сечение 1 и 2 участок струйки произвольной дли-ны. Пусть площадь 1-ого сечения dA1, скорость в нем V1, давление Р1, высота расположения центра масс сечения Z1. Во втором сечении: dA2, V2, P2, Z2. За бесконечно малое время dt, участок струйки переместится в положение 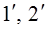. Применим к массе жидкости в объеме струйки теорему механики. Работа сил прилож.к телу равна приращению кинетич. энергии этого тела. В рассмотренном случае такими силами явл.: сила давления и сила тяжести. Работа силы давления в первом сечении положит. Т.к. направление силы совпадает с направл.движения и равно:

.

Работа силы давления во втором сечении отрицательна т.к. направление силы и перемещение противопол.

Результирующая работа сил давления:

Силы тяжести заштрихованных элементов = между собой и опред: 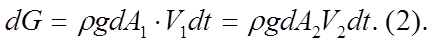Работа силы тяжести выражается 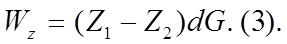Приращение кинетической энергии =: Учитывая, что согласно названной теореме механике =: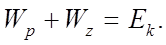

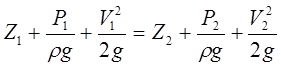Разделим уравнение 5 на dG и получим: Проинтегрируем: уравнение Бернулли для элементарной струйки идеальной не сжимаемой жидкости. 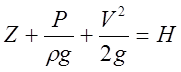- наз. полным напором. Уравнение Бернулли данное записано для двух сечений:

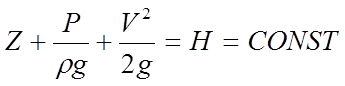
Т. образом для идеальной движущейся жидкости сумма трех напоров геометр. ‘Z’, пьезометрического 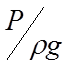и скоростного есть величина постоянная вдоль струйки – это геометрический смысл уравнения Бернулли. Энергетический смысл уравнения Бернулли для элементарной струйки жидкости заключается в постоянстве вдоль струйки полной удельной энергии жидкости, следовательно уравнение Бернулли выражает закон сохранения механической энергии идеальной жидкости.

Дата добавления: 2015-05-23