Гидроудар в частично заполненной вертикальной трубе

Рассмотрим развитие гидроудара в вертикальной трубе, часть которой возле заглушки уже заполнена неподвижной жидкостью. Случай, когда жидкостью заполнена часть трубы возле входа, рассмотрен выше и описывается формулами (13) (для сверхтекучей жидкости) и (16)–(18) (с учётом гидравлического трения).

Когда поток сталкивается с неподвижной жидкостью возле заглушки, гидроудар возникает немедленно и распространяется в обе стороны — к заглушке и ко входу в трубу. При этом его сила (скачок давления) в соответствии с формулой Жуковского определяется лишь скоростью перед остановкой. Но зато длительность, а, следовательно, и полная энергия, определяется геометрией, то есть расстояниями от места столкновения до заглушки и до входа в трубу.

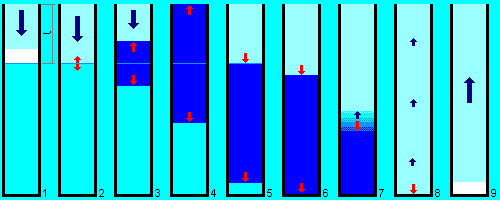
Схема развития гидравлического удара при заполнении потоком уже частично заполненной жидкостью вертикальной трубы. Голубым цветом обозначена внешняя среда с исходным давлением, светло-голубым — область пониженного давления, синим — область повышенного давления (зона гидроудара). Синие стрелки показывают перемещение вещества среды (жидкости), красные — перемещение границы зоны повышенного давления (без существенного перемещения вещества). Светло-синяя линия отмечает исходный уровень неподвижной жидкости на расстоянии l от входа в трубу. Цифрами обозначены этапы развития процесса.

Разберём этапы развития этого процесса более подробно (в скобках указаны соответствующие цифры на рисунке). Заполняющий трубу поток (этап 1) натыкается на неподвижную жидкость. Поскольку деваться ей некуда, она сразу оказывает жёсткое сопротивление вновь прибывшей жидкости и останавливает её. Поэтому в месте столкновения кинетическая энергия потока сразу начинает переходить в потенциальную энергию упругой деформации, что сопровождается повышением давления — в месте столкновения возникает гидравлический удар (этап 2). Ударная волна от места удара начинает распространяться в обе стороны — как по набегающему потоку, останавливая всё новые его части, так и по неподвижной жидкости, сжимая её (этап 3). Впрочем, благодаря малой сжимаемости жидкостей при таком сжатии вещество почти не перемещается, поэтому неподвижная жидкость фактически остаётся там же, где была до начала гидроудара. Через какое-то время фронты сжатия, движущиеся в разные стороны, достигнут заглушки и выхода из трубы. Когда фронт сжатия достигнет заглушки, не произойдёт ничего, а вот когда фронт сжатия достигнет входа в трубу, ударная волна выйдет в среду и начнёт рассеиваться (этап 4), также как и в фазе (4) «классического» гидроудара.

Затем граница области сжатия начнёт откатываться внутрь трубы (этап 5 здесь и фаза (5) «классического» гидроудара). Однако пока передний фронт зоны сжатия ещё не достиг заглушки, сильного обратного движения жидкости за задним фронтом сжатия нет. Это обусловлено тем, что импульс исходного потока продолжает распространяться к заглушке до тех пор, пока не достигнет её. При этом на переднем фронте зоны сжатия жидкость как бы слегка «проминается», и всё это выглядит как перетекание освобождающейся энергии деформации с заднего фронта зоны сжатия в сжимаемую жидкость на её переднем фронте. Таким образом, картина несколько отличается от «классики» — возле заглушки мы имеем ещё невозмущённую несжатую неподвижную жидкость, к ней стремительно движется фронт сжатия, а от входа трубы с той же скоростью и в том же направлении уже движется фронт спада давления.

Когда передний фронт зоны сжатия достигает заглушки (этап 6), он как бы «упирается» в неё, поскольку впереди больше нет жидкости, которую можно было бы сжать. Теперь «разряжаемая» жидкость на заднем фронте области сжатия действительно начинает двигаться обратно ко входу в трубу, поскольку для освобождаемой энергии деформации остаётся только один вариант — превратиться в кинетическую энергию жидкости. Однако при этом надо разогнать и всю жидкость на участке от заднего фронта зоны сжатия до входа в трубу, что занимает некоторое время. Поэтому задний фронт давления несколько «размывается», как показано на этапе 7. Впрочем, по мере разгона жидкости в обратном направлении эта «размытость» заднего фронта становится всё менее выраженной и, в конце концов, картина приближается к «классической» фазе (6). Этот механизм преобразует относительно мощный, но короткий импульс первичного удара в более слабый, но имеющий «стандартную» (т.е. ту же, что при заполнении пустой трубы) длительность — такую же, как и во всех последующих циклах.

Наконец, развитие процесса полностью переходит в «классические» рамки: зона сжатия сокращается (этап 7) и в последнюю очередь исчезает возле заглушки — этап 8, «классическая» фаза (6). Затем наступает фаза разрежения, которая при достаточной силе гидроудара сопровождается отрывом жидкости от заглушки — этап 9, «классическая» фаза (7). Однако за счёт «размывания» заднего фронта и необходимости разгона при обратном ходе всей жидкости в трубе скорость при этом будет меньше исходной скорости потока, даже в идеальном случае — когда нет необратимых потерь.

Остаётся выяснить вопрос, насколько изменится сила гидроудара по сравнению с пустой трубой? Здесь картина более сложная, чем в рассмотренной чуть выше горизонтальной трубе. Пока зона сжатия расширяется и её передний фронт не достиг заглушки, за счёт «проминания» невозмущённой жидкости, сжимаемость которой равна сжимаемости останавливаемой жидкости, скачок давления будет в корень из двух раз меньше, чем при гидроударе непосредственно в заглушку (кинетическая энергия преобразуется в деформацию, распространяющуюся в обе стороны от места начального столкновения). Однако если изначально неподвижной жидкости в трубе меньше, чем вновь прибывшей, то, когда передний фронт зоны сжатия достигает заглушки, сила гидроудара (скачок давления) там достигает тех же значений, что и в случае пустой трубы.

А вот длительность первого сжатия в любом случае будет меньше и на участке от места возникновения гидроудара до заглушки равна

t_C1 = 2 · l / c (21),

где t_C1 — длительность стадии сжатия первого цикла гидроудара; l — расстояние от места возникновения гидроудара до входа в трубу; с — скорость распространения ударной волны в трубе, рассчитываемая по формуле (5).

Длительность первого сжатия на участке от входа в трубу до места возникновения гидроудара будет такой же, как и при заполнении пустой трубы и должна рассчитываться по формуле (9).

Для всех последующих циклов гидроудара длительности стадий сжатия и расширения определяются уже полной длиной трубы от входа до заглушки и не отличаются от заполнения пустой трубы. Поэтому они должны рассчитываться по тем же формулам (6)—(10). Однако энергия гидроудара по сравнению с пустой трубой уменьшается в число раз, равное соотношению длительностей первой стадии сжатия

k_E = t_C1 / t_CЗ = (2 · l / c) / (2 · L / c) = l / L (22),

где k_E — отношение энергии гидроудара в частично заполненной трубе к той же энергии при заполнении пустой трубы; t_C1 — длительность стадии сжатия первого цикла гидроудара в частично заполненной трубе, рассчитываемая по формуле (21); t_CЗ — длительность стадии сжатия у заглушки при гидроударе в пустой трубе, рассчитываемая по формуле (6); l — расстояние от места возникновения гидроудара до входа в трубу; L — полная длина от заглушки до входа; с — скорость распространения ударной волны в трубе.

Соответственно, скорости жидкости и скачок давления при всех последующих стадиях гидроудара в частично заполненной трубе будут отличаться от случая пустой трубы в √k_E раз (квадратный корень из соотношения энергий). С учётом того, что кинетическая энергия здесь прямо пропорциональна массе жидкости, а в масса жидкости в трубе с неизменным сечением — её длине, это соотношение определяется квадратным корнем из отношения полной длины трубы к длине её незаполненной части √(l / L).

Мы рассмотрели столкновение потока с неподвижной жидкостью. Однако жидкость, в которую ударяет поток, может и сама двигаться в ту или иную сторону. Но здесь мы уже имеем дело со столкновением потоков.

Дата добавления: 2015-05-23