Робота і потужність струму. Закон Джоуля-Ленца

Розглянемо ділянку кола опором R до якої прикладена напруга U і по якій тече струм силою І. Із означення електричної напруги (3.160) визначимо елементарну роботу по переміщенню по колу елементарного заряду dq

. (3.211)

Із означення сили струму (3.156) визначимо елементарний заряд

. (3.212)

Підставимо вираз (3.212) у формулу (3.211)

. (3.213)

Проінтегруємо вираз (3.203) і отримаємо формулу роботи електричного струму

. (3.214)

У випадку постійного струму, коли , , 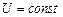робота електричного струму визначається за формулою

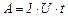. (3.215)

Потужність рівна роботі виконаній за одиницю часу

. (3.216)

Підставимо (3.213) у формулу (3.216). Отримаємо формулу потужності струму

. (3.217)

Якщо електричний струм не виконує роботу проти зовнішніх сил і не змінюється внутрішня енергія провідника то, як випливає з першого закону термодинаміки, робота струму рівна кількості теплоти, яка виділяється в провіднику

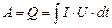. (3.218)

З закону Ома для ділянки кола випливає

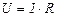. (3.219)

Підставимо (3.219) у формулу (3.218)

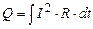. (3.220)

У випадку постійного струму формула (3.220) набере вигляду

. (3.221)

Формули (3.220) і (3.221) – це закон Джоуля-Ленца в інтегральній формі: кількість теплоти, яка виділяється в провіднику при проходженні електричного струму, прямо пропорційна квадрату сили струму, опору провідника і часу проходження струму

Розглянемо циліндричний провідник з площею поперечного перерізу , довжиною 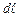, по якому тече струм силою 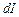. Тоді за час 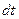в ньому виділиться кількість теплоти , яка згідно з формулою (3.221) рівна

. (3.222)

З формул (3.164) і (3.159) отримаємо

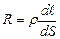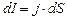; . (3.223)

Підставимо (3.223) у формулу (3.222)

(3.224)

де 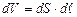– об’єм провідника.

Питомою тепловою потужністю струму називається фізична величина, рівна кількості теплоти, яка виділяється в одиниці об’єму провідника за одиницю часу

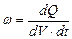. (3.225)

Підставимо (3.224) у формулу (3.225) отримаємо

. (3.226)

Формула (3.226) – це закон Джоуля-Ленца в диференціальній формі: питома теплова потужність струму прямо пропорційна питомому опору провідника і квадратові густини струму.

Використовуючи формули (3.173) вираз (3.226) можне бути представлений у вигляді

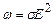. (3.227)

Формули (3.227) – це другий варіант закону Джоуля-Ленца в диференціальній формі: питома теплова потужність струму прямо пропорційна питомій електропровідності провідника і квадрату напруженості електричного поля.

Дата добавления: 2015-05-23