Деформаційні сили. Гідродинаміка. Теорі подібності та фізико-технологічні процеси СТ. 35

Дисипативна енергія

Правило важелів Архімеда

У книжці «Про рівновагу і визначення центра ваги плоских фігур» Архімед уперше доводить відоме правило важеля: нерівні тягарі перебувають у рівновазі на важелі, якщо відстані центрів тягарів від. точки опори важеля обернено пропорційні їх вагам. У цій самій праці" Архімед визначає центри ваги прямокутників, паралелограмів, трикутників і т. д.

Є всі підстави припускати, що тут він установив саме поняття центра ваги аме поняття центра ваги тіла: це така точка, в якій досить підтримати тіло, щоб воно було в рівновазі у будь-якому положенні.

Дисипати́вна систе́ма (або дисипати́вна структу́ра) — відкрита нелінійна система, яка є далекою від стану термодинамічної рівноваги. Така система є нерівноважною завдяки розсіянню енергії, одержуваної ззовні. Внаслідок самоорганізації у таких системах можуть виникати стійкі структури, які існують за умови постійної дисипації, тобто втрати системою енергії. З появою складної впорядкованої структури в системі зростає ентропія, яка компенсується негативним потоком ентропії зовні.

Дисипативна структура здійснює постійний обмін речовиною та енергією із середовищем, в котрому вона народилася, та є структурно стійкою у ньому. Класичним прикладом таких структур є комірки Бенара, винайдені у 1900 році. Ці комірки утворюються у воді, котру постійно підігрівають знизу, за рахунок конвекційних потоків. Як тільки система переходить в рівноважний стан, тобто підігрівання води припиняють, ці структури зникають. Термін дисипативних структур уперше використав бельгійський вчений Ілля Пригожин.

Дисипативна система також може називатися нерівноважною або стаціонарною відкритою системою. Прикладами такої системи із спонтанною самоорганізацією окрім ефекту Бенара може бути реакція Бєлоусова-Жаботинського з її автоколиваннями, лазер із синфазним випромінюванням атомів тощо. Біологічне життя теж може вважатися прикладом дисипативної системи.

1 ) Пру́жна деформа́ція — деформація, що не викликає незворотних змін у структурі тіла.

При пружній деформації тіло повертає собі попередні розміри й форму при знятті напруження.

Закон Гука встановлює лінійну залежність між деформацією й механічними напруженнями.

Закон Гука справедливий для малих пружних деформацій.

У своїй найпростішій формі закон Гука записується для деформації довгого тонкого стрижня або пружини

сила, прямо пропорційна лінійному видовженню пружини відносно рівноважного положення:

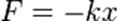
де F — сила, k — коефіцієнт жорсткості, х — видовження.

. Для випадку лінійного навантаження закон Гука має вигляд:

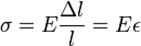де: σ — механічне напруження, визначається, як сила, що припадає на одиницю площі поперечного перерізу тіла;

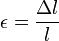— величина відносної деформації (відносне видовження);

E — модуль Юнга.

Дата добавления: 2015-05-23