Диференціальна формула Остроградського-Гауса. Рівняння Пуасона і Лапласа і оператор Лапласа

Лінії напруженості електричного поля. Потік вектора напруженості, та вектора електричної індукції. Теорема Остроградського Гауса для знаходження, параметрів поля заряженої площини, сфери, кулі та циліндра.

Потенціалточкового заряду

Скалярний потенціал

Скалярнийпотенціал векторного поля (Частіше просто потенціал векторного поля) - цескалярнафункція така, що у всіхточкахобластівизначення поля

де позначаєградієнт . У фізицізазвичайпотенціаломназивають величину, протилежну за знаком (потенціалсили, потенціалелектричного поля).

Лінії напруженості електростатичного поля (силові лінії) незамкнені: починаються на позитивних зарядах, а закінчуються на негативних; вони неперервні й не перетинаються.
Напруженість поля точкового заряду:
.
Електричне поле між двома паралельними різнойменно зарядженими пластинами, а також поле плоского конденсатора однорідні, тобто напруженість кожного із цих полів у будь-якій точці однакова і чисельно, і за напрямком.

Ознакою однорідності поля є паралельність його силових ліній. 

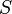Електричний потік (ElectricFlux)- потік вектора електричної індукції () через поверхню (не обов'язково замкнуту).

Відомо, що напруженість електричного поля залежить від властивостей фізичного середовища, в якому діє електричне поле (). Тому для повної характеристики електричного поля вводиться фізична величина, котра має назву електричної індукції (або електричного зміщення).

У випадку слабких^[1] електричних полів, відсутності анізотропії та дисперсії, вектор електричної індукції та напруженість електричного поля зв'язані формулою:

,

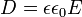де 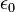- діелектрична стала. Очевидно, що електрична індукція є векторна величина, що не залежить від властивостей середовища (оскільки останні просто входять в неї):

.

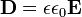Електричний потік вектора електричної індукції через довільну поверхню 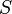в певній точці визначається через одиничний вектор нормалі 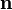до цієї поверхні в цій точці:

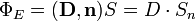
Звичайно, ця формула справедлива у випадку плоскої поверхні 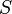. В загальному випадку довільної поверхні необхідно брати інтегральний вираз для потоку вектора електричної індукції:

.

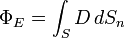Фо́рмула Острогра́дского — формула, котораявыражаетпоток векторного поля через замкнутуюповерхностьинтегралом от дивергенцииэтого поля по объёму, ограниченномуэтойповерхностью:

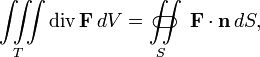
то есть интеграл от дивергенции векторного поля 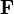, распространённый по некоторомуобъёмуT, равенпотоку вектора через поверхностьS, ограничивающуюданныйобъём.

Формула применяется для преобразованияобъёмногоинтеграла в интеграл по замкнутойповерхности.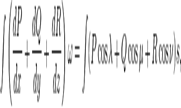

В работеОстроградского формула записана в следующемвиде:

гдеω и s — дифференциалыобъёма и поверхностисоответственно. В современной записи ω = d Ω — элементобъёма, s = dS — 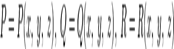элементповерхности. — функции, непрерывныевместесосвоимичастнымипроизводнымипервогопорядка в замкнутойобластипространства, ограниченногозамкнутойгладкойповерхностью.

Рівняння Пуассона - неоднорідне еліптичне рівняння в часткових похідних другого порядку.

Зокрема, в електростатиці рівняння, яке описує потенціал електричного поля в системі зарядів, заданих густиною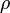

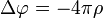
Рівняння Лапласа — однорідне лінійне рівняння в часткових похідних другого порядку еліптичного типу.

.

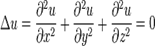Функції, які задовільняють рівнянню Лапласа, називаються гармонічними.

Відповідне неоднорідне рівняння називається рівнянням Пуассона.

Дата добавления: 2015-05-23