Для фотонного газу

2.7

2.6

2.5

2.4

2.3

Основні поняття й означення.

Об'єкт дослідження в термодинаміці в узагальненому вигляді називають термодинамічною системою. Під термодинамічною системою розуміють деяку речовину, здебільшого задану параметрами Її стану, оскільки вона бере участь у процесах зміни й перетворення енергії.

Рівноважним станом називають такий стан системи, параметри якої — температура, тиск і об'єм — сталі.

Рівноважним процесом називають неперервну послідовність рівноважних станів системи. Такий процес можна здійснити лише при нескінченно повільних змінах стану системи.

До основних понять і величин у термодинаміці належать внутрішня енергія, робота і кількість теплоти.

Внутрішня енергія. Під внутрішньою енергією системи розуміють сумарну енергію всіх видів частинок, з яких складається система. Сюди входить кінетична і потенціальна енергія молекул, енергія коливальних рухів атомів у молекулах, енергія електронних оболонок в атомах та іонах і внутрішньоядерна енергія. До внутрішньої не відноситься енергія системи як цілого, яку вона може мати в результаті механічного руху або взаємодії з іншими системами. Інакше кажучи, внутрішньою енергією називають сумарну енергію мікрочастинок, з яких складається система. Внутрішня енергія є функцією стану системи, тобто змінюється із зміною стану системи і однозначно визначається тими самими параметрами, що й система. У термодинаміці практичне значення має не сама внутрішня енергія, а її зміна з переходом системи з одного стану в інший.

Робота. У термодинаміці поняття про роботу набуває ширшого змісту, бо стан системи і відповідно її внутрішню енергію, як функцію стану, можна змінювати завдяки виконанню і макроскопічної, і мікроскопічної роботи. Остання здійснюється без будь-якого видимого переміщення тіл, що взаємодіють, її інакше називають теплообміном.

Кількість теплоти. макроскопічна робота і теплообмін — способи зміни внутрішньої енергії системи. Кількісною мірою процесу макроскопічної роботи є фізична величина, яка також називається роботою. Кількісною мірою процесу теплообміну є фізична величина, що називасться кількістю теплоти. Кількість теплоти і робота, як величини, що визначаютьзміну внутрішньої енерііі системи, у реальних процесах можуть бути взаємно зв’язаними і визначати одна одну.

Перший закон термодинаміки

Цей закон містить три величини: внутрішню енергію U, роботу А і теплоту Q. Перш ніж сформулювати сам закон, встановимо фізичне значення цих величин.

Перший закон термодинамики стверджує, що приріст внутрішньої енергії макросистеми при її переході з початкового стану 1 в кінцеве 2 рівно сумі досконалої над системою роботи А' всіх зовнішніх макроскопічних сил і кількості переданого системі тепла Q:

U₂ – U₁ = Q + А'. (1.1)

Оборотні І Необоротні Процеси

За почином Р. Клаузіуса термодинамічні процеси поділяють на два вили.

До процесів першого виду відносять такі, які відбуваються “самі по собі”. Такими, наприклад, є перехід теплоти від тіла з вищою темперагурою до тіла з нижчою температурою, зниження центра маси системи, перетворення механічного руху в тепловий тощо. Ці процеси називають природними.

До процесів другого виду належать такі, які «самі по собі» не відбуваються, для їх здійснення треба використати додатково процеси першого виду. Ці процеси називають штучними.

Поділ процесів на природні й штучні в термодинаміці тісно пов'язаний з поняттям про оборотні й необоротні процеси.

Оборотним називають такий процес, який може відбуватися в обох напрямках. Після завершення такого процесу в прямому і зворотному напрямах сисгема повертається в початковий стан і в навколишньому середовищі не залишається ніяких слідів. Якщо процес не має перелічених вище ознак, то його називають необоротним.

Другий початок термодинаміки

1. Клаузіус (1850): неможливий мимовільний перехід тепла від менш до більш нагрітого тіла, або неможливі процеси, єдиним кінцевим результатом яких був би перехід тепла від менш до більш нагрітого тіла.

2. Кельвін (1851): неможливі процеси, єдиним кінцевим результатом яких було б перетворення тепла цілком в роботу.

2-ге формулювання Кельвіна так: вічний двигун 2-го роду неможливий, бо неможливо створити тепловий двигун з ККД η = 1.

Третій закон термодинаміки

4. Теорема Нернста (1906). Ця теорема cтверджує, що при наближенні температури до абсолютного нуля ентропія макросистеми також прямує до нуля: S → 0 при T → 0 (3.4)

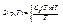(3.5)

Звідси слідує, що при Т → 0 теплоємність С _р всіх макросистем повинна теж прагнути нуля (інакше інтеграл не буде сходитися).

Теорема Нернста не може бути логічно виведена з перших двох початків, тому її часто називають третім початком термодинаміки

Властивості ентропії

1. Ентропія - функція стану.

2. Ентропія - величина адитивна: ентропія макросистеми рівна сумі ентропії її окремих частин.

3. Одна з найважливіших властивостей ентропії полягає в тому, що ентропія замкнутої (тобто теплоізольованої) макросистеми не зменшується - вона або зростає, або залишається постійною.

Принцип зростання ентропії замкнутих систем являє собою ще одне формулювання другого початку термодинаміки.

Величина зростання ентропії в замкнутій макросистемі може служити мірою безповоротності процесів, що протікають в системі. В граничному випадку, коли процеси мають оборотний характер, ентропія замкнутої макросистеми не міняється.

4. Приріст ентропії при необоротному процесі між двома рівноважними станами 1 і 2. Безпосередньо рахувати ентропію по необоротному процесу абсолютно неможливо. Але ентропія - функція стану. Цим ми і скористаємося, провівши між станами 1 і 2 який-небудь оборотний процес, який немає нічого спільного з реальним необоротним процесом.

5. Зростання ентропії при змішенні газів. Хай в двох половинах теплоізольованої судини об'ємом V знаходяться два ідеальні гази, 1 і 2, розділених перегородкою. Після видалення перегородки починається необоротний процес змішення газів. Врешті-решт він припиняється, і система приходить в рівноважний стан, в якому обидва гази рівномірно перемішані. Температура в кінцевому стані буде така ж, оскільки система теплоізольована і гази ідеальні. Знаходимо, що при V ₁ = V ₂ приріст ентропії кожного газу Δ S _1,2 = νR ln 2, тобто сумарний приріст ентропії системи Δ S = 2 vR ln2.

Приріст Δ S > О, що природно, оскільки процес змішення істотно необоротний (зворотний процес - саморозділення суміші двох газів - абсолютно неймовірний).

Статистична фізика - це розділ фізики, в якому вивчають властивості макросистем, виходячи з індивідуальних властивостей складових частинок макросистеми і взаємодій між ними. Опис руху кожної частинки макросистеми (а їх близько 10²²¸10²³) - завдання абсолютно немислиме. Натомість статистична фізика оперує з середніми значеннями параметрів дуже великого числа частинок.

Основу статистичної фізики складає теорія ймовірності. ймовірність події, що цікавить нас, характеризується кратністю її повторення. Якщо в N випадках і-а подія відбувається N_і раз, то ймовірністю Р_і цієї події називають величину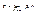

Тепер звернемося до обчислення ймовірності складних подій. Розглянемо дві основні теореми: про складання і множення ймовірності. Найпростіше це зрозуміти за допомогою грального кубика.

1. Теорема про складання ймовірності полягає в тому, що ймовірність того, що в результаті N кидань кубика випаде іабо k, рівна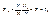

2. Теорема про множення ймовірності. Знайдемо ймовірність того, що при двох киданнях кубика випаде послідовно i і k (або навпаки). Розглянемо N подвійних кидань. Нехай перший кубик з кожної пари кидків дав і в N_iвипадках (отже Р_i» N_i/N).

Тепер виділяємо з цих N_i випадків ті N_k випадків, коли другий кубик давав k (отже Р_k» N_k/N_i).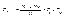

Середні значення випадкових величин. Знаючи ймовірності появи різних результатів вимірювання дискретної величини х, можна знайти їх середнє значення áхñ. За визначенням середнього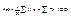

Функція розподілу. Розглянемо випадок, коли випадкова величина х має безперервний характер (наприклад, швидкості молекул). Для цього розіб'ємо всю область зміни х на окремі інтервали і рахуватимемо число попадань випадкової величини в той або інший інтервал. Інтервали повинні бути щоб уникнути помітних флуктуації достатньо великими, щоб в кожному інтервалі число попадань було N_i >> 1 і щоб з допомогою (2.2) можна було визначити ймовірність попадання випадкової величини в даний інтервал. Разом з тим, інтервали повинні бути достатньо невеликими, щоб детальніше характеризувати розподіл величини х.

Отже, ми маємо достатньо велике число досить невеликих інтервалів і, припустимо, нам відома ймовірність Рх попадання в той або інший інтервал Dх. Сама величина DРх досить мала, тому як характеристику випадкової величини беруть відношення DРх/Dх, яке для достатньо малих Dх не залежить від величини самого інтервалу Dх.

Це відношення при Dх: ® 0 Про називають функцією розподілу f(x) випадкової величини х: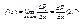

Мікроканонічний розподіл

Якщо система знаходиться в стані рівноваги, то середні значення будь-яких її параметрів не будуть залежати від часу. Тому функція розподілу повинна залежати тільки від інтегралів руху системи. Основним інтегралом руху є повна механічна енергія системи Е або функція Гамільтона Н. Відповідно, найпростіший загальний вид функції розподілу буде w(х)=w(Н).

Функція Гамільтона залежить від 6H змінних системи х і від зовнішніх параметрів а, тобто Н(х,а). безпосередній висновок функції розподілу з механіки поки ще не розв'язана проблема.

Розглянемо адіабатичну, тобто замкнуту систему з певною енергією. Отриманий розподіл w(х) записують так:

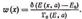
Знайдена функція розподілу для адіабатичної системи називається мікроканонічним розподілом (мал. 27).

Канонічний розподіл Гіббса

Тепер знайдемо функцію розподілу w (х) для ізотермічної системи, що знаходиться в термостаті. При цьому ізотермічну систему можна розглядати як деяку частину ще більшої системи. Для цієї частини великої системи і потрібно знайти функцію розподілу w(х).

Канонічний розподіл Гіббса запишеться у вигляді

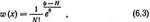
Оскільки з N частинок можливо N! перестановок, той фазовий простір системи тотожних частинок слід зменшити в N! раз.

Термодинамічний зміст параметрів канонічного розподілу.

модуль канонічного розподілу Q володіє наступними двома властивостями термодинамічної температури:

1) Термодинамічні системи з однаковими температурами знаходяться в рівновазі між собою.

2. Величина, зворотна температурі, є інтегруючим множником для зміни кількості теплоти системи dQ.

Поняття статистичної температури має на увазі наявність системи частинок. Не можна, наприклад, застосовувати поняття температури для однієї або дуже малого числа частинок. Статистична температура характеризує розподіл систем у фазовому просторі, будучи модулем канонічного розподілу.

Параметр канонічного розподілу y має зміст «вільної енергії». Дійсно, в термодинаміці показується, що узагальнені сили рівні похідній від вільної енергії по відповідній узагальненій координаті, узятій із зворотним знаком.

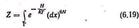
називається інтегралом станів і грає важливу роль в статистичній фізиці.

Інтеграл станів відображає внутрішній стан системи, оскільки інтеграція проводиться по всіх мікростанах системи. Іншими словами Z. є функцією стану і залежить від a_k і Q.

Інтеграл станів придбаває особливо важливе значення у зв'язку з тим, що з його допомогою можна обчислити для будь-якої статистичної системи вільну енергію, а отже, і ряд інших термодинамічних параметрів.

Розподіл Максвела

Уявимо собі простір швидкостей з прямокутними координатними осями, по яких відкладатимемо значення проекцій їх V_x, V_y, V_z окремих молекул. Тоді швидкості кожної молекули відповідатиме крапка в цьому просторі - кінець вектора V. Із-за зіткнень молекул положення крапок стрімко мінятимуться, але їх розподіл в цілому залишатиметься незмінним, оскільки макросистема знаходиться в термодинамічній рівновазі.

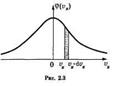
Унаслідок рівноправності всіх напрямів руху розташування крапок щодо початку координат буде сферично симетричним. Тому щільність крапок може залежати тільки від модуля швидкості V (але не від об’єму v).

Графік функції j(v_x) зображений на рис. 2.3. Він співпадає з гауссовою кривою похибок. Площа тонованої смужки на рис 2.3 - це ймовірність того, що проекція швидкості молекули лежить в інтервалі, (v_х, v_х + dv_x).

Функція (2.16) нормована на одиницю, тобто площа під кривою j(v_x)

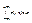= 1 (2.18)

Розподіл Больцмана

У відсутність зовнішніх сил середня концентрація n молекул газу в стані термодинамічної рівноваги усюди однакова. Якщо ж газ знаходиться в зовнішньому силовому полі, ситуація стає іншою. n = n₀e^-U/kT (2.36)

Цей закон і виражає розподіл Больцмана.

Швидкості руху молекул. До них відносяться три швидкості: найімовірніша v_ймов, середня ávñ і середньоквадратична v_кв.

Найімовірніша швидкість відповідає максимум функції розподілу Р(v). Ця швидкість визначається з умови dF/dv = О, звідки слідує

v_{ймов = 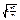=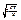} (2.22)

Середня швидкість за визначенням

ávñ = 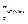= = 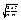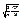(2.23)

Середньоквадратична швидкість vкв = 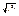; вона знаходиться з умови áv2ñ = 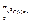= 3 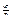звідки v_{кв = =}

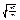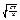
Закон розподілу Максвелла-Больцмана як частинні випадки канонічного розподілу Гіббса

Розподіли Максвела і Больцмана є складовими частинами єдиного розподілу, званого розподілом Гіббса (це питання детально розглядається в спецкурсах по статистичній фізиці, і ми обмежимося тільки згадкою цього факту).

Обидва розібраних нами розподіли можна об'єднати в один закон розподілу Максвелла-Больцмана, згідно якому число dN молекул, проекції швидкості яких і їх координати лежать в інтервалах

(v_x, v_x + dv_x), (v_y, v_y + dv_y), (v_z, v_z + dv_z)

(x, x + dx), (y, y + dy), (z, z + dz)

визначається виразом

dN = A exp 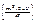dv_xdv_ydv_zdxdydz (2.41)

де нормуючий множник A = n₀(m/2pkT)^3/2, v2 = v_x² + v_y² + v_z², U = U(x, y, z).

Частинки з напівцілим спіном, їх називають ферміонами; вони підкоряються статистиці Фермі-Дірака, У статистиці Фермі-Дірака в кожному квантовому стані може знаходитися не більш одна частинка (принцип Паулі), а в статистиці Бозе-Ейнштейна - будь-яке число частинок.

Квантові розподіли. Ці розподіли є функціями f(ε_i), що визначають середні числа частинок в одній фазовій комірці з енергією ε_i або функції заповнення комірок:

для ферміонів 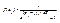(4.2)

Тут μ - так званий хімічний потенціал (деяка характерна енергія, значення якої можна знайти з умови нормування: сумарне число частинок у всіх фазових комірках повинне бути рівне повному числу N частинок макросистеми).

1. Для ферміонів функція f(ε_i) не може бути більше одиниці, а для бозонів її значення може бути будь-яким (f ≥ 0).

2. Якщо f << 1, то в знаменниках розподілів можна нехтувати одиницею, і формула переходять в 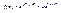(4.4)

3. У макросистемі рівні енергії ε_i частинок квазінепреривні (розташовані дуже щільно). Тому індекс i у ε_i можна опустити.

4. Для бозонів значення м в (4.3) не можуть бути позитивними, інакше при ε_i < μ виявиться, що f < 0, а це позбавлено фізичного значення. Таким чином, для бозонів μ ≤ 0. У макросистем із змінним числом бозонів (до числа яких відносяться, наприклад, фотони) μ = 0, і формула (4.3) переходить в 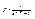(4.5) Для ферміонів подібного обмеження не існує.

Розподіл Фермі-Дірака

для електронів в металі

Вільні електрони в металі. Електропровідність металів обумовлена, як відомо, наявністю в них електронів, які ми називаємо вільними. Вони не пов'язані з конкретними атомами і можуть практично вільно переміщатися в межах зразка. У першому наближенні вільні електрони можна розглядати як ідеальний газ з ферміонів в прямокутній потенційній ямі.

Перш за все розглянемо поведінку електронного газу при температурі Т = 0. В цьому випадку функція (4.2) приймає наступні значення:

f (ε ≤ μ) = 1, f (ε > μ) = 0 (4.9)

Відповідний графік показаний на рис. 4,1, з якого видно, що заповнені всі стани з енергією е < м, а стани з е > м виявляються незайнятими.

Стани квантовані, і енергетичні рівні є дискретними, але розташовані настільки густо, що енергетичний спектр можна рахувати, як вже мовилося, квазібезперервним (див. задачу 4.2).

Питома теплоємність – це відношення кількості теплоти (Q), необхідної для нагріву тіла, до різниці температур (ΔТ) тіла і до його маси (m), тобто це така кількість теплоти, яка необхідна для нагріву 1 г речовини на один градус: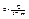

Частинки з цілим спіном - бозони; вони підкоряються статистиці Бозе-Ейнштейна.

У статистиці Фермі-Дірака в кожному квантовому стані може знаходитися не більш одна частинка (принцип Паулі), а в статистиці Бозе-Ейнштейна - будь-яке число частинок.

Квантові розподіли. Ці розподіли є функціями f(ε_i), що визначають середні числа частинок в одній фазовій комірці з енергією ε_i або функції заповнення комірок:

для бозонів 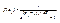(4.3)

Тут μ - так званий хімічний потенціал (деяка характерна енергія, значення якої можна знайти з умови нормування: сумарне число частинок у всіх фазових комірках повинне бути рівне повному числу N частинок макросистеми).

1. Для ферміонів функція f(ε_i) не може бути більше одиниці, а для бозонів її значення може бути будь-яким (f ≥ 0).

2. Якщо f << 1, то в знаменниках розподілів можна нехтувати одиницею, і формула переходять в

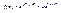(4.4)

3. У макросистемі рівні енергії ε_i частинок квазінепреривні (розташовані дуже щільно). Тому індекс i у ε_i можна опустити.

4. Для бозонів значення м в (4.3) не можуть бути позитивними, інакше при ε_i < μ виявиться, що f < 0, а це позбавлено фізичного значення. Таким чином, для бозонів μ ≤ 0. У макросистем із змінним числом бозонів (до числа яких відносяться, наприклад, фотони) μ = 0, і формула (4.3) переходить в

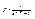(4.5)

Для ферміонів подібного обмеження не існує.

Розподіл Бозе-Ейнштейна

Рівноважне теплове випромінювання в замкнутій порожнині є сукупністю стоячих електромагнітних хвиль з дискретними частотами. Ейнштейн припустив, і це підтвердилося експериментом, що саме випромінювання представляє собою фотонний газ, газ ідеальний. У фотонів спін рівний одиниці. Значить це бозони, а вони підкоряються статистиці Бозе-Ейнштейна.

Число фотонів в порожнині не зберігається, воно залежить від температури. А для систем із змінним числом бозонів, хімічний потенціал μ = 0, і функція (4.3) приймає вигляд (4.5), тобто

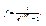(4.21)

Для фотонів ε = hν і р = hν / c, тому число квантових станів (фазових осередків) в інтервалі частот (ν, ν + d ν) з розрахунку на одиницю об'єму фотонного газу рівне згідно (4.7)

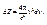(4.22)

Графік розподілу фотонів по частотах, тобто dn/dn, показаний на рис. 4.11. Площа під кривою рівна повному числу n фотонів з розрахунку на одиницю об'єму фотонного газу.

Закони рівноважного випромінювання.

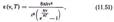
Ця формула називається формулою Планка для спектральної густини енергії рівноважного випромінювання. Кількість енергії, випромінюваної абсолютно чорним тілом у вигляді електромагнітних хвиль в інтервалі частот від n до n+dn рівно

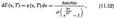
Ввівши нову змінну

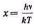
і скориставшись значенням певного інтеграла для повної енергії випромінювання, отримаємо:

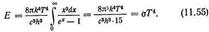
Формула Планка у вигляді (11.52) дозволила пояснити всі закони випромінювання абсолютно чорного тіла, підтвердивши тим самим висунуту Планком «гіпотезу квант». Ми отримали відомий закон Стефана - Больцмана.

Рівність

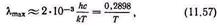
показуюче, що довжина хвилі, яка відповідає максимуму випромінювання в спектрі абсолютно чорного тіла, змінюється обернено пропорційно до абсолютної температури. Це і є закон зсуву Вина.

Виявляється, формула Планка при певних припущеннях переходить і в інші відомі формули. Так, у випадку

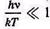
розкладаючи знаменник формули (11.51) в ряд і обмежуючись першим членом розкладання, одержуємо класичну формулу Релея - Джинса:

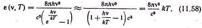
У разі ж, коли

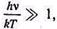
нехтуючи одиницею в знаменнику, отримаємо іншу відому формулу Вина для спектральної густини при великих частотах:

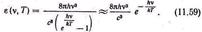
Дата добавления: 2015-05-23