
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Кінематика обертального руху
|
|
|
|
Кутова швидкість. Поворот тіла можна представити направленим відрізком уздовж осі обертання – вектором повороту 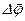 . Довжина цього вектора дорівнює куту повороту, а напрямок визначається за правилом правого гвинта (правилом свердлика) (див. рис. 7). Тільки дуже малі повороти задовольняють
. Довжина цього вектора дорівнює куту повороту, а напрямок визначається за правилом правого гвинта (правилом свердлика) (див. рис. 7). Тільки дуже малі повороти задовольняють

Рис. 7
правилу векторного додавання і, отже, є векторами. Якщо за час 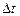 виконується поворот
виконується поворот 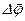 , то середня кутова швидкість
, то середня кутова швидкість
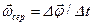 . (1.31)
. (1.31)
Миттєва кутова швидкість
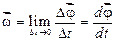 . (1.32)
. (1.32)
Таким чином, вектор кутової швидкості дорівнює першій похідній від вектора повороту за часом і направлений уздовж осі обертання і пов’язаний з напрямком обертання правилом правого гвинта (правилом свердлика). Модуль вектора кутової швидкості
 . (1.33)
. (1.33)
При  відбувається рівномірний обертальний рух, для якого вводяться такі величини: T – період обертання (час одного оберту) та n = 1 /T – частота обертання. Тоді кутова швидкість
відбувається рівномірний обертальний рух, для якого вводяться такі величини: T – період обертання (час одного оберту) та n = 1 /T – частота обертання. Тоді кутова швидкість
w=2pn =2p /T. (1.34)
Кутове прискорення. Якщо за час 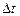 приріст кутової швидкості
приріст кутової швидкості  , то середнє кутове прискорення
, то середнє кутове прискорення
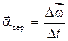 (1.35)
(1.35)
Миттєве кутове прискорення
 (1.36)
(1.36)
Вектор кутового прискорення 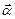 характеризує зміну кутової швидкості в одиницю часу і дорівнює першій похідній від кутової швидкості за часом. Вектор
характеризує зміну кутової швидкості в одиницю часу і дорівнює першій похідній від кутової швидкості за часом. Вектор 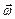 може змінюватися як за рахунок зміни швидкості обертання, так і за рахунок повороту осі обертання у просторі. Якщо напрямок осі обертання у просторі залишається незмінним, то модуль кутового прискорення
може змінюватися як за рахунок зміни швидкості обертання, так і за рахунок повороту осі обертання у просторі. Якщо напрямок осі обертання у просторі залишається незмінним, то модуль кутового прискорення
 . (1.37)
. (1.37)
У формулі (1.37) a – проекція вектора  на вектор
на вектор 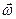 , тобто алгебраїчна величина (може мати різні знаки) (див. рис. 8).
, тобто алгебраїчна величина (може мати різні знаки) (див. рис. 8).
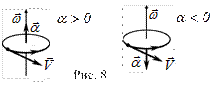
При a > 0 вектори 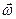 і
і  мають однаковий напрямок – обертання є прискореним, при a < 0 вектори
мають однаковий напрямок – обертання є прискореним, при a < 0 вектори 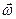 і
і  протилежно направлені – обертання сповільнене.
протилежно направлені – обертання сповільнене.
Зв’язок між лінійними і кутовими швидкостями і прискореннями має вигляд
V=wR; (1.38) 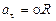 ; (1.39)
; (1.39)
де R – радіус кола, по якому рухається матеріальна точка. Формулу (1.38) можна переписати у векторному вигляді:
 , (1.40)
, (1.40)
де 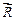 – радіус-вектор матеріальної точки у площині обертання, а хрестик позначає векторний добуток векторів.
– радіус-вектор матеріальної точки у площині обертання, а хрестик позначає векторний добуток векторів.
Відступ. Є дії додавання векторів, віднімання векторів, два види добутків (скалярний і векторний), але немає дії ділення вектора на вектор.
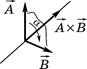
Рис. 9
Скалярний добуток  двох векторів – це скаляр:
двох векторів – це скаляр:  , де a – кут між векторами
, де a – кут між векторами  і
і  .
.
Векторний добуток 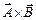 двох векторів – це вектор, модуль якого
двох векторів – це вектор, модуль якого 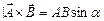 , а
, а
напрямок перпендикулярний площині, яку проведено через вектори  і
і 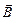 , і пов’язаний з напрямком найменшого повороту від
, і пов’язаний з напрямком найменшого повороту від  до
до 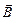 правилом правого гвинта (див. рис. 9).
правилом правого гвинта (див. рис. 9).
|
|
|
|
|
Дата добавления: 2015-05-23; Просмотров: 2962; Нарушение авторских прав?; Мы поможем в написании вашей работы!