Задачі для самостійного розв'язування

1.00. Залежність пройденого тілом шляху S від часу t дається рівнянням S = At – Bt ² + Ct ³, де А = 2 м/с, В = 3 м/с² і С = 4 м/с³. Знайти: а) залежність швидкості v і прискорення a від часу t; б) відстань S, пройдену тілом, швидкість v і прискорення a через час t = 2 с після початку руху.

1.01. Залежність пройденого тілом шляху S від часу t дається рівнянням S = A – Bt + Ct ³, де А = 6 м, В = 3 м/с і С = 2 м/с³. Знайти середню швидкість < v > і середнє прискорення < a > тіла для інтервалу часу 1с £ t £ 4с

1.02. 1.02. Залежність пройденого тілом шляху S від часу t дається рівнянням S = A + Bt+ Ct ², де А = 3 м, В = 2 м/с, С = 1 м/с². Знайти середню швидкість < v > і середнє прискорення < a > за другу і третю секунди його руху.

1.03. Рівняння руху матеріальної точки (пройдений шлях x за час t) має вигляд: x = At + Вt ² + Сt ³, де А = 5 м/с, B = 0,2 м/с², C = 0,1 м/с³. Визначити швидкість точки в моменти часу t ₁ = 2 с і t ₂ = 4 с, а також середню швидкість в інтервалі часу від t ₁ до t ₂ .

1.04. Визначити шлях, який проходить частинка, що рухається по прямолінійній траєкторії впродовж 10 с, якщо її швидкість змінюється за законом v = 30 + 2 t. В момент часу t _o = 0, S = 0.

1.05. Швидкість матеріальної точки, що рухається вздовж осі X, визначається рівнянням v_x = 0,2 – 0,1 t. Знайти координату точки в момент часу t = 10 с, якщо в початковий момент часу вона знаходилась в точці x_o = 1

1.06. Рух двох матеріальних точок виражається рівняннями:
x ₁ =А ₁ + B ₁ t +С ₁ t ²та x ₂ = А ₂ +B ₂ t +С ₂ t ², де A ₁= 20 м; А ₂ = 2 м;
В ₁ = В ₂ = 2 м/с; С ₁ = – 4 м/с²; C ₂= 0,5 м/с². В який момент часу t швидкості цих точок будуть однаковими? Визначити швидкості v ₁ і v ₂ та прискорення a ₁ і a ₂ точок в цей момент.

1.07. Рух двох матеріальних точок виражається рівняннями:
x ₁ = А ₁ t +B ₁ t ² +С ₁ t ³ та x ₂ = А ₂ t + B ₂ t ² +С ₂ t ³, де A ₁ = 4 м/с; В ₁ = 8 м/с²; С ₁ = –16 м/с³; А₂ = 2 м/с; В ₂ = – 4 м/с²; C ₂= 1 м/с³. В який момент часу t прискорення цих точок будуть однакові? Знайти швидкості v ₁ і v ₂ точок в цей момент.

1.08. Рух точки по прямій задано рівнянням x = At+Вt ², де А =2м/с; В = – 0,5 м/с². Визначити середню швидкість < v > руху точки в інтервалі часу від t ₁ = 1 с до t ₂= 3 с.

1.09. Рух точки по прямій задано рівнянням x= Аt+Вt ², де А= 6м/с; В = – 0,125 м/с². Визначити середню швидкість < v > руху точки в інтервалі часу від t ₁ = 2 с до t ₂= 6 с.

1.10. Літак для зльоту повинен мати швидкість v = 100 м/с. Визначити час розбігу і прискорення, якщо довжина розбігу S = 600 м. Рух літака при цьому вважати рівноприскореним.

1.11. Автомобіль рухається зі швидкістю v ₁ = 25 м/с. На шляху S = 40 м проводиться гальмування, після якого швидкість зменшилась до v ₂ = 15 м/с. Вважаючи рух автомобіля рівносповільненим, знайти модуль прискорення і час гальмування.

1.12. Визначити час піднімання ліфта у висотному будинку, вважаючи його рух при розгоні і гальмуванні рівнозмінним з прискоренням a = 1 м/с², а на середній ділянці – рівномірним зі швидкістю v = 2 м/с. Висота підйому h = 60 м.
1.13. Визначити початкову швидкість тіла, кинутого вертикально вгору, якщо відмітку висоти h = 60 м воно проходило двічі з проміжком часу D t = 4 с. Опір повітря не враховувати.

1.14. Тіло, кинуте вертикально вниз із початковою швидкістю v_o = 19,6 м/с, за останню секунду пройшло n = ¼ частину всього шляху. Визначити час падіння тіла і його кінцеву швидкість.

1.15. Визначити кутове прискорення маховика, частота обертання якого за час здійснення N = 20 повних обертів зросла рівномірно від n ₁=1 об/с до n₂ =5 об/с.

1.16. Диск радіусом r = 10 см, що знаходився в стані спокою, почав обертатися з постійним кутовим прискоренням e = 0,5 рад/с. Знайти тангенціальне a _t , нормальне a_n і повне прискорення точок на ободі диска в кінці другої секунди після початку обертання.

1.17. Диск обертається з кутовим прискоренням e = –2 рад/с. Скільки обертів N зробить диск при зміні частоти обертання від n ₁= 4 с ^–1 до n ₂ =1,5 с ^–1. Знайти час t, протягом якого це станеться.

1.18. Колесо обертається з кутовим прискоренням e = 2рад/с. Через час t = 0,5 с після початку руху повне прискорення точки, що лежить на ободі колеса a =13,6 см/с². Знайти радіус R колеса.

1.19. Точка рухається по колу радіусом R = 10 см з постійним тангенціальним прискоренням a _t= 5 см/с. Через який час після початку руху нормальне прискорення точки буде дорівнювати тангенціальному?

1.20. Похила площина, що утворює кут a = 25^o з площиною горизонту, має довжину l = 2 м. Тіло, рухаючись рівноприскорено, зісковзнуло з цієї площини за час t = 2 с. Визначити коефіцієнт тертя k тіла і площини.

1.21. Через нерухомий блок перекинута тонка нерозтяжна нитка, на кінцях якої підвішені два вантажі масами m ₁= 200 г і m ₂ = 300 г. Який шлях пройде кожен з вантажів за 1 с? Вважати, що блок обертається без тертя. Масою блока знехтувати.

1.22. Щоб визначити коефіцієнт тертя k між дерев'яними поверхнями, брусок поклали на дошку і стали піднімати один кінець дошки доти, доки брусок не почав ковзати по дошці. Це сталося, коли кут нахилу дошки становив a = 14^o. Чому дорівнює k?

1.23. Аеростат масою m = 250 кг почав опускатись із прискоренням а = 0,20 м/с². Визначити масу баласту, яку потрібно скинути за борт, щоб аеростат одержав таке ж прискорення, спрямоване вгору. Опором повітря знехтувати.

1.24. В нижній точці мертвої петлі реактивний літак рухається зі швидкістю v = 1200 км/год. Визначити, якого перевантаження (відношення сили тиску на сидіння до сили тяжіння) зазнає пілот, якщо діаметр петлі 1 км.

1.25. Нерухомий блок підвішений до динамометра. Через блок перекинутий невагомий шнур, на кінцях якого укріплені вантажі масами m ₁ = 2 кг і m ₂= 8 кг. Яким буде показ динамометра при русі вантажів?

1.26. Дві гирі, які мають маси m ₁= 3 кг і m ₂= 6,8 кг, висять на кінцях нитки, перекинутої через нерухомий блок. Легка гиря знаходиться на 2 м нижче від важкої. Гирі почали рухатись без початкової швидкості. Через який час вони будуть на однаковій висоті?

1.27. Кліть вагою Р = 3×10⁴ Н піднімається з прискоренням a = 0,49 м/с. Визначити силу натягу канату, за допомогою якого піднімається кліть. Якою буде сила натягу канату за рівномірного руху кліті вгору і вниз?

1.28. Автомобіль, маса якого m = 1000 кг, рухається зі швидкістю v ₁ = 36 км/год по опуклому мосту, радіус кривини якого R = 50 м. З якою силою тисне автомобіль на середину мосту? З якою найменшою швидкістю v ₂ має рухатись автомобіль, щоб у верхній точці він зовсім не тиснув на міст?

1.29. Кулька масою m = 20 г прикріплена до кінця невагомого стрижня довжиною l = 40 см, який рівномірно обертається у вертикальній площині довкола іншого кінця, роблячи 10 обертів за секунду. Знайти силу натягу стрижня, коли кулька проходить верхню і нижню точку своєї траєкторії.

1.30. Циліндр діаметром D = 12 см, що має масу m = 3 кг, лежить боковою поверхнею на горизонтальній площині. Визначити момент інерції циліндра відносно осі, що проходить по лінії контакту з площиною.

1.31. Обчислити момент інерції тонкого обруча радіусом r = 0,5 м і масою m = 3 кг відносно осі, що проходить через кінець діаметра перпендикулярно до площини обруча.

1.32. Визначити момент інерції суцільної кулі масою m =10 кг і радіусом R = 0,1 м відносно осі, дотичної до кулі.

1.33. Визначити момент інерції Землі відносно осі обертання, вважаючи її кулею радіусом R = 6 400 км і масою M = 6×10²⁴ кг.

1.34. До ободу однорідного суцільного диска радіусом R = 0,5 м прикладена постійна дотична сила F = 100 Н. При обертанні диска на нього діє момент сил тертя М = 2 Н × м. Визначити масу диска, якщо відомо, що його кутове прискорення постійне і дорівнює e = 12 рад/с.

1.35. Махове колесо, момент інерції якого J = 245 кг×м², обертається з частотою n = 20 об/с. Після того, як на колесо перестав діяти обертовий момент сил, воно зупинилось, зробивши N = 1000 обертів. Знайти момент сил тертя M _тер і час гальмування t від припинення дії обертального моменту до зупинки колеса.

1.36. На вал масою m ₁ = 20 кг намотана нитка, до кінця якої прив'язали вантаж масою m ₂ = 1 кг. Визначити прискорення вантажу, що опускається під дією сили тяжіння. Масою нитки і тертям знехтувати.

1.37. Маховик, що являє собою диск масою m = 10 кг і радіусом
R =10 см, вільно обертається довкола осі, яка проходить через центр, з круговою частотою w = 6 рад/с. При гальмуванні маховик зупиняється через час t = 5 с. Визначити гальмівний момент.

1.38. Маховик масою m ₁ = 1 кг укріплений на шківі радіусом r = 5 см і масою m ₂ = 200 г, який приводиться в обертання з допомогою гирі, що опускається, масою m ₃ = 500 г, прив'язаної до кінця намотаної на шків мотузки. Через який час швидкість маховика досягне n = 5 об/с? Вважати, що вся маса маховика розподілена по його ободу на відстані R = 40 см від осі обертання. Тертям та масою мотузки знехтувати.

1.39. На барабан радіусом R = 10 см намотана нитка, до кінця якої прив'язаний вантаж масою m = 0,5 кг. Знайти момент інерції барабана, якщо вантаж опускається з прискоренням а = 1,0 м/с.

1.40. Молот масою m = 20 кг, піднятий на висоту h = 1,2 м, вільно падає на ковадло. Знайти середню силу удару молота в ковадло, якщо удар непружний, а тривалість удару Dt = 0,005с?

1.41. З якою швидкістю v ₁ повинна летіти куля масою m ₁ = 1кг, щоб після її удару об візок з піском, який стоїть на рейках, візок дістав швидкість u = 2 cм/c? Маса візка m ₂ = 30 кг, куля рухається паралельно до рейок, удар повністю непружний.

1.42. Дві однакових платформи рухаються одна за одною (без тертя) з однією і тією ж швидкістю v_o. На задній платформі знаходиться людина масою m. В певний момент людина перескочила на передню платформу зі швидкістю u відносно своєї платформи. Знаючи, що маса кожної платформи дорівнює М, знайти швидкості, з якими будуть рухатись обидві платформи після стрибка людини.

1.43. На краю нерухомої платформи маси М знаходиться двоє людей, маса кожного з них дорівнює m. Нехтуючи тертям, знайти швидкість платформи після того, як обоє людей зіскочать з однією й тією ж горизонтальною швидкістю u відносно платформи: а) одночасно; б) один за одним.

1.44. На платформі установлено безвідкатну гармату, з якої робиться постріл вздовж залізничного полотна під кутом a = 45^o до горизонту. Визначити початкову швидкість снаряду, якщо відомо, що після пострілу платформа відкотилась на відстань S = 3 м. Маса платформи з гарматою M = 2×10⁴ кг, маса снаряду m = 10 кг, коефіцієнт тертя кочення між колесами платформи і рейками k = 0,002.

1.45. Яка енергія пішла на деформацію двох кульок масами m ₁ = m ₂ = 4 кг, що зіткнулися, якщо вони рухались назустріч одна одній зі швидкостями v ₁=3 м/с і v ₂ = 8 м/с, а удар був прямий і непружний.

1.46. Дві кулі масами m ₁ = 0,2 кг і m₂ = 0,8 кг, підвішені на двох паралельних нитках довжиною l = 2 м, дотикаються одна до одної. Менша куля відводиться на кут a = 90^о від початкового положення і відпускається. Знайти швидкість куль після зіткнення, вважаючи удар абсолютно непружним. Яка частина механічної енергії піде на нагрівання куль?

1.47. Після вибуху гранати, що летіла зі швидкістю v = 8 м/с, утворились два осколки. Осколок, маса якого становила 0,3 від маси гранати, продовжував рухатись у попередньому напрямку зі швидкістю v ₁ = 30 м/с. Визначити швидкість другого осколка.

1.48. На підніжку вагонетки, що рухається прямолінійно зі швидкістю v = 2 м/с, стрибає людина масою m = 60 кг у напрямку, перпендикулярному до ходу вагонетки. Маса вагонетки М = 240 кг. Визначити швидкість вагонетки разом з людиною.

1.49. Два човни масою М = 100 кг кожен ідуть паралельним курсом назустріч один одному з однаковою швидкістю v = 5 м/с. Коли човни зустрічаються, з першого човна на другий перекидають вантаж масою m = 25 кг, а потім з другого човна в перший перекидають такий же вантаж. Визначити швидкості човнів.

1.50. Якою кінетичною енергією володіло тіло масою m = 2 кг, якщо воно піднялось по похилій площині з кутом нахилу a = 30^о на висоту h = 1 м? Коефіцієнт тертя між тілом і похилою площиною k = 0,1.

1.51. На тонкій нитці підвішений пружинний пістолет так, що ствол розміщений горизонтально. На який кут відхилиться нитка після пострілу, якщо куля масою m = 20 г при вильоті зі ствола має швидкість v = 10 м/с? Маса пістолета М = 200 г.

1.52. Знайти роботу, яка виконується при підніманні вантажу масою m = 10 кг по похилій площині з кутом нахилу a = 45^о на відстань S = 2 м, якщо час піднімання вантажу t = 2 c, а коефіцієнт тертя k = 0,1.

1.53. Парашутист масою m = 70 кг здійснює затяжний стрибок і через час t = 14 c має швидкість v = 60 м/с. Вважаючи рух парашутиста рівноприскореним, знайти роботу по подоланню опору повітря.

1.54. Кулька для гри в настільний теніс радіусом r = 15 мм і масою m = 5 г занурена у воду на глибину h = 30 см. Коли кульку відпустили, вона вистрибнула з води на висоту h ₁ = 10 cм. Яка кількість тепла виділиться внаслідок тертя кульки і води?

1.55. Яку роботу потрібно здійснити, щоб маховик у вигляді диска масою m = 100 кг і радіусом R = 0,4 м, який знаходився у стані спокою, став обертатися з частотою n = 20 об/c?

1.56. Обчислити кінетичну енергію диска масою т = 2 кг, що котиться без ковзання по горизонтальній поверхні зі швидкістю v = 2 м/с.

1.57. Куля котиться без ковзання по горизонтальній поверхні. Повна кінетична енергія кулі Т = 14 Дж. Визначити кінетичну енергію Т ₁ поступального і Т ₂ обертового руху кулі.

1.58. Однорідний тонкий стрижень довжиною l = 1 м може вільно обертатися відносно горизонтальної осі, що проходить через його кінець. Стрижень відхилили на кут j = 60^о і відпустили. Визначити кутову швидкість w і лінійну швидкість v нижнього кінця стрижня в момент проходження ним положення рівноваги.

1.59. Кінетична енергія маховика, що обертається, дорівнює Т = 1 кДж. Під дією постійного гальмівного моменту маховик почав обертатись рівносповільнено і, зробивши N = 80 обертів, зупинився. Визначити момент сил тертя.

1.60. Точка здійснює коливання за законом х = А sinwt. В певний момент часу зміщення точки виявилось рівним х ₁ = 5 см. Коли фаза коливань збільшилась удвічі, зміщення стало рівним х ₂ = 8 см. Знайти амплітуду А коливань.

1.61. Точка здійснює гармонічні коливання. Найбільше зміщення точки х _max=10 см, найбільша швидкість v _max= 20 cм/c. Знайти циклічну частоту коливань w і максимальне прискорення точки a _max.

1.62. Початкова фаза гармонічного коливання j = 0. При зміщенні точки від положення рівноваги х ₁ = 2,4 см швидкість точки v ₁ = 3 см/с, а при зміщенні х ₂ = 2,8 см її швидкість v ₂ = 2 cм/c. Знайти амплітуду А і період Т цього коливання.

1.63. Точка здійснює гармонічне коливання. Період коливання Т = 2с, амплітуда А = 5 см, початкова фаза j = 0. Знайти швидкість v в момент часу, коли зміщення точки від положення рівноваги х = 2,5 см.

1.64. Визначити амплітуду вимушених коливань вантажу масою т = 0,2кг, підвішеного на пружині жорсткістю k = 20 Н/м, якщо діє змушуюча сила з амплітудою А = 2 Н і частотою удвічі більшою від власної частоти коливань вантажу, а коефіцієнт згасання b = 0,5 с^–1.

1.65. Визначити період коливань вантажу на пружинній вазі, якщо у стані рівноваги він зміщує стрілку ваги на Dх = 2 см від нульової поділки, яка відповідає ненавантаженій пружині.

1.66. Кулька масою т = 200 г підвішена на пружині i коливається з частотою n = 5 Гц. Визначити коефіцієнт жорсткості пружини.

1.67. У скільки разів зменшиться повна енергія коливань секундного маятника за t = 5 хв, якщо логарифмічний декремент згасання D = 0,031?

1.68. Амплітуда коливань камертона за час t = 15 c зменшилась у 100 разів. Знайти коефіцієнт згасання коливань.

1.69. Знайти частоту коливань вантажу масою т = 0,2 кг, підвішеного на пружині і зануреного в олію, якщо коефіцієнт тертя в олії r = 0,5 кг/c, а жорсткість пружини k = 50 Н/м.

1.70. Знайти швидкість поширення звукових коливань в повітрі, довжина хвилі яких l = 1 м, а частота коливань n = 340 Гц. Чому дорівнює максимальна швидкість зміщення частинок повітря, якщо амплітуда коливань А = 0,2 мм?

1.71. На якій відстані від джерела коливань, які здійснюються за законом синуса, в момент часу t = T/ 2 зміщення точки від положення рівноваги дорівнює половині амплітуди? Швидкість поширення коливань v = 340 м/с. Період коливань Т = 10^–3 с.

1.72. У скільки разів зміниться довжина ультразвукової хвилі при переході хвилі зі сталі у мідь, якщо швидкості поширення ультразвуку у міді і сталі відповідно дорівнюють v ₁= 3600 м/cі v ₂ =5500 м/с?

1.73. Дві точки знаходяться на відстані х = 50 см одна від одної на прямій, вздовж якої поширюється хвиля із швидкістю v = 50 м/с. Період коливань Т = 0,05 с. Знайти різницю фаз Dj коливань у цих точках.

1.74. Плоска звукова хвиля має період Т = 3 мс, амплітуду А = 0,2 мм і довжину хвилі l = 1,2 м. Для точок середовища, віддалених від джерела коливань на відстань х = 2 м, знайти зміщення x(х,t), швидкість 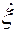і прискорення для моменту часу t = 7 мс. Початкову фазу коливань вважати рівною нулю.

1.75. Визначити різницю фаз Dj коливань джерела хвиль, що знаходиться в пружному середовищі і точки цього середовища, яка знаходиться на відстані х = 2 м від джерела. Частота коливань дорівнює n = 5 Гц; хвилі поширюються із швидкістю v = 40 м/c.

1.76. Хвиля поширюється в пружному середовищі зі швидкістю v= 100 м/c. Найменша відстань між точками середовища, фази яких протилежні, дорівнює Dх = 1 м. Визначити частоту n коливань.

1.77. Визначити швидкість v поширення хвилі у пружному середовищі, якщо різниця фаз коливань двох точок середовища, які знаходяться одна від одної на відстані Dх = 10 см, дорівнює Dj = p /3. Частота коливань n= 25 Гц.

1.78. Знайти зміщення х від положення рівноваги точки пружного середовища, віддаленої від джерела коливань на відстань l = l /12, для моменту часу t=T/ 6. Амплітуда коливань А = 0,05 м.

1.79. Зміщення від положення рівноваги точки, яка віддалена від джерела коливань на відстань l = 4 см, в момент часу t = T/ 6 дорівнює половині амплітуди. Знайти довжину біжучої хвилі.

Дата добавления: 2015-05-23