Коефіцієнт рангової кореляції

Нехай групу учнів ранжували у відповідності із їхніми здібностями, виявленими на уроках музики та математики. Позначимо дітей буквами від А до J і випишемо наступні дві послідовності рангів:

Учні	A	B	C	D	E	F	G	H	I	J
Математика
Музика

Розглянемо питання, чи існує залежність між математичними та музичним здібностями. Зрозуміло, що чіткої залежності не існує. Однак деякі учні посідають майже однакові місця в обох рядах. Наявність (відсутність) зв’язку між цими показниками стане більш очевидною, якщо ми розташуємо елементи першого ряду в порядку збільшення (у послідовності натуральних чисел):

Учні	I	F	C	B	J	E	A	H	G	D
Математика
Музика

Необхідно визначити ступінь зв’язку між цими двома послідовностями або, іншими словами, визначити тісноту рангової кореляції. Методика побудови відповідного коефіцієнта кореляції 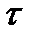наступна. Коефіцієнт кореляції повинен володіти наступними властивостями. (методика побудови відповідного коеф. кореляції)

1. Якщо між послідовностями порядкових оцінок існує повна відповідність, тобто кожний елемент займає одне і те ж місце в обох рядах, то 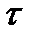має бути рівним +1, що означає повну рангову кореляцію.

2. Якщо існує повна негативна залежність, тобто якщо в одній послідовності оцінки розташовані у зворотній послідовності у порівнянні з іншою, то 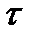=-1, що означає повну негативну кореляцію;

3. В інших випадках 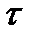лежить між граничними значеннями; можна стверджувати, що збільшення 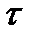від -1 до +1 у певному розумінні характеризує відповідність між двома послідовностями порядкових оцінок.

У першій послідовності виділимо деяку пару рангів, наприклад А і В. Їхні значення 7 і 4 утворюють зворотній порядок величин (прямим порядком називатимемо порядок натурального ряду 1,…,10); парам, що утворюють прямий порядок, будемо присвоювати значення +1, а тим, що утворюють зворотній порядок, – присвоюватимемо значення -1. У другій послідовності ранги А та В утворюють прямий порядок (5,7). Відповідно, цій парі присвоюється значення 1.

Перемноживши значення, що присвоюються цим парам у першій та другій послідовностях, отримаємо добуток, рівний -1. Зрозуміло, що для довільної пари значень цей добуток буде рівний +1 у тому випадку, коли відповідні значення утворюють в обох послідовностях однаковий порядок рангів, і -1, якщо порядки рангів ­ різні.

Можна сказати, що ми приписуємо значення +1 та -1 залежно від того, чи узгоджуються між собою порядки пари в обох послідовностях.

Сума значень, рівних +1 (назвемо її Р),, а сума значень, рівних -1 (назвемо її Q), Додавши ці два числа, отримаємо загальну суму приписаних значень S 3.Якщо б усі пари мали однаковий порядок, то кожне із приписуваних значень було б позитивним; відповідно максимальне значення S було б рівне. Міркуючи аналогічно, приходимо до висновку, що мінімальне значення S повинно складати -45. Таким чином, значення 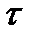рівне:

.

Ця величина близька до нулю; звідси випливає, що кореляція між двома послідовностями рангів дуже мала. Нульове значення 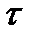може інтерпретуватися як свідчення незалежності рядів.

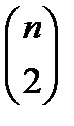Розглянемо загальний випадок, коли є дві послідовності рангів, кожна із яких містить членів; кількість пар, що підлягають порівнянню, дорівнює кількості способів, за допомогою яких можна вибрати два предмети з набору, що містить предметів; ця величина рівна ; іноді її позначають . Вказане число характеризує найбільшу можливу суму приписаних значень; така її величина може бути досягнута тільки тоді, коли порядок рангів в обох послідовностях співпадатиме. Позначивши загальну кількість приписаних значень буквою 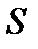, введемо наступне визначення коефіцієнта кореляції: 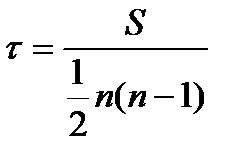. (1)

Нехай 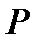та 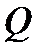позначають відповідно суми приписуваних позитивних та негативних значень (так, що 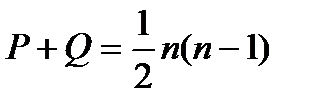); тоді можна записати еквівалентні формули для обчислення 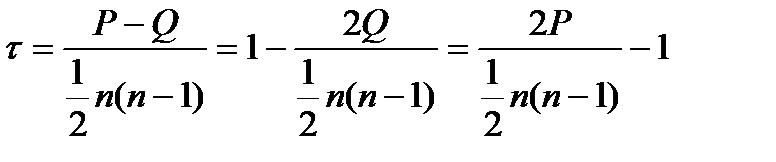. (2)

Для того, щоб знайти 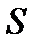(що рівносильне знаходженню та ), не потрібно відтворювати описану вище послідовність дій. Існують і простіші способи. Найбільш простий із них, очевидно, наступний.

Розглянемо формулу (2). У тих випадках, коли одна послідовність рангів є натуральним рядом 1, 2,..., 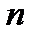, то оцінки, що приписуються кожній парі значень цього ряду, позитивні. Відповідно, значення +1, що входять доданками до суми 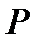, будуть приписуватися тільки тим парам другого ряду, котів утворюють прямий порядок. Потрібно тільки перерахувати їх

Дата добавления: 2015-05-24