Та молекулярної фізики 3 страница

Дані вимірів і обчислень занести до таблиці:

	l	α	Δt	T	ω	Δω	A
Теоретичне Вимірювання 1 Вимірювання 2 Вимірювання 3		-	-			-	-

Дайте відповіді на запитання:

1. Як залежить точність виконання законів гармонічних коливань від кута відхилення математичного маятника?

2. Приймаючи відносну похибку 0,03, оцінити за даними табл.1, для яких кутів можна застосовувати закони гармонічних коливань?

Лабораторна робота № 11.

Вивчення затухаючих коливань на прикладі фізичного маятника.

Прилади та приладдя: установка з фізичним маятником і градусною шкалою, лінійка, секундомір.

Мета роботи: Визначення параметрів затухаючих коливань.

Коротка теорія і метод вимірювань

Фізичним маятником називається тіло, вільно підвішене на нерухому вісь в точці, що не співпадає з центром інерції тіла. У відсутності тертя і при малих амплітудах коливань рух фізичного маятника можна розглядати як гармонічне коливання, яке здійснюється за законом синуса або косинуса:

x = A sin ωt, (1)

де A - амплітуда коливання, ω - циклічна частота коливання, t – час, x - відхилення від положення рівноваги по горизонтальному напрямку.

Коливання фізичного маятника може буте зведено до коливання математичного маятника, для якого період коливання T і циклічна частота ω обчислюються за формулами:

T = 2π 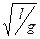, ω = 2π / T, (2)

де l - довжина математичного маятника, g - прискорення вільного падіння.

Довжина математичного маятника, період коливань якого співпадає з періодом коливань фізичного маятника називається приведеною довжиною фізичного маятника. Якщо виміряти період коливань фізичного маятника, то за формулою (2) можна обчислити приведену довжину фізичного маятника:

l = gT² / 4π². (3)

При наявності тертя коливання маятника з плином часу затухають - зменшується амплітуда коливань. Рівняння затухаючих коливань має вигляд:

x = A₀ exp (- βt) sin ω₃t, (4)

де A = A₀ exp (- βt) - амплітуда коливань, що зменшується з плином часу, A₀ - початкова амплітуда, β - коефіцієнт затухання, ω₃ - циклічна частота затухаючих коливань, яка менша за частоту ω незатухаючих - власних коливань:

ω₃ = . (5)

Графік затухаючих коливань подано на рис.1.

Ступінь затухання коливань характеризують декрементом затухання - відношенням двох послідовних амплітуд, взятих через період. Натуральний логарифм декремента затухання:

Δ = ln (A_n/ A_n+1) = ln [ A₀e^{- β t} / A₀e^{- β (t + T)} ] = β t (6)

В даній роботі фізичний маятник являє собою стрижень з віссю обертання на шариковому підшипнику. Зміна періоду коливань маятника здійснюється зміною положення муфти, надітої на стрижень.

Завданнями роботи є визначення приведеної довжини фізичного маятника і вивчення закону затухаючих коливань. Неважко збагнути, що логарифмічний декремент затухання можна визначити за формулою

Δ = ln (A₀ / A_n)/n, (7)

де A_n - амплітуда n -го коливання.

Порядок виконання роботи:

Завдання 1.

1. Ознайомитися з установкою. Встановити муфту верхнім краєм проти верхньої риски на стрижні і виміряти відстань r від осі обертання до центра муфти. Відхилити маятник на 15-20˚ від положення рівноваги і в трьох дослідах виміряти секундоміром період коливань T.

2. Повторити заміри за пунктом 1 двічі, опускаючи кожного разу муфту на 5-10 см. Результати вимірювань і розрахунків подати в табл. 1. Порівняти значення r і l.

Таблиця 1

№	r	T	l	r-l	(r-l)/l

Завдання 2.

1. Залишаючи муфту в третьому положенні, відхилити маятник на 15-20˚ і при коливаннях помітити відхилення початкового і кінцевого коливань. Зробити подібні вимірювання тричі. Кожного разу обчислити значення початкової і кінцевої амплітуди за формулою A_n = l sin α_n..

2. Знайти в кожній серії вимірів відношення початкової амплітуди до шостої (три значення). Згідно з (6) розрахувати логарифмічний декремент затухання як Δ = ln (A₆ / A₀)/6 = 2,3 lg (A_n / A_n+1)/6.

3. Визначити коефіцієнт затухання β=Δ/T, використовуючи T з останнього рядка табл.1.

4. Дані вимірів та розрахунків за пп.3-5 подати в табл. 2. Обчислити циклічну частоту коливання за співвідношенням ω = 2π / T.

Таблиця 2.

№	An	An+1	An / An+1	Δ	T	β
				- - -	- - -	- - -
Середні значення

Записати рівняння затухаючих коливань (4), підставляючи в нього знайдені числові значення.

Дайте відповіді на запитання:

1. Як змінюється різниця між положенням центру муфти і приведеною довжиною фізичного маятника при опусканні муфти?

2. Від чого залежить та як можна виміряти коефіцієнт затухання в цій роботі?

3. Як залежить період затухаючих коливань в даній роботі від положення муфти на стрижні фізичного маятника?

Лабораторна робота № 12.

Дослідження прискорення вільного падіння за допомогою оборотного маятника.

Прилади та приладдя: оборотний маятник, секундомір, міліметрова лінійка, призма для находження центра інерції фізичного маятника.

Мета роботи: засвоїти метод визначення прискорення вільного падіння за допомогою оборотного фізичного маятника.

Коротка теорія та метод вимірювання

Фізичним маятником називають будь-яке тіло, що коливається під дією сили тяжіння відносно осі, що не перетинає його центр інерції.

Період коливань фізичного маятника може бути визначений за тією ж формулою, що і математичного маятника

T = 2π (1)

де g - прискорення вільного падіння, l - так звана приведена довжина фізичного маятника.

Приведена довжина фізичного маятника може бути виражена через його момент інерції I відносно осі обертання, відстань d від m осі обертання до центра інерції і масу маятника:

l = I / md (2)

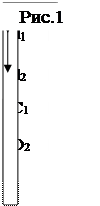
Оборотний фізичний маятник (див. рис.1) складається з металевого стержня, вздовж якого можуть переміщуватися тягарі і опорні призми, що служать для підвішування маятника. Якщо маятник підвісити на одну, а потім на другу призму, то періоди коливань в цих двох випадках, згідно з співвідношенням (2), можуть бути подані у вигляді:

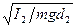T₁= 2π ; T₂ = 2π (3)

де d₁і d₂ - відстані від точок опори до центра інерції маятника С (рис.1); I₁ і I₂ - моменти інерції маятника відносно точок опори.

Згідно з теоремою Штайнера

I₁ = I₀ + md₁² ; I₂ = I₀ + md₂² , (4)

де I₀ - момент інерції маятника відносно осі, що проходить через інерції тіла. Із (3) з урахуванням (4) можна одержати такі співвідношення:

T₁² = 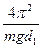(I₀ + md₁²); T₂ ² = 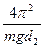(I₀ + md₂²).

Підставляючи І₀ із першого в друге рівняння, одержуємо

g = 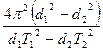. (5)

Це – розрахункова формула для визначення g в першому завданні. При використанні в другому завданні рівності періодів коливань T₁= T₂ = T оборотного маятника на точках опори O₁ і O₂ (рис.1), коли рівні і їх приведені довжини l₁ = l₂ = l, із (3) і (4) одержуємо:

l = . (6)

Визначаючи із (6) I₀, приходимо до виразу

I₀ = md₁d_2. (7)

Підставляючи значення I₀ із (7) в (6), одержуємо співвідношення, що дозволяє визначити приведену довжину фізичного маятника за прямими вимірюваннями:

l = d₁+ d₂. (8)

Знаючи приведену довжину фізичного маятника і вимірюючи період коливань T₁, за формулою (1) можемо визначити прискорення вільного падіння:

g = 4π² l / T² (9)

Порядок виконання роботи:

Завдання 1.

1. Розмістивши тягарі так, як вказано на рис. 1., відхилити кінець маятника на 3-4см, тричі визначити секундоміром час ста повних коливань, розрахувати значення T₁і T₂.

2. Поклавши маятник на ребро спеціальної призми і домігшись рівноваги, визначити положення центра інерції – точки С (рис.1) і виміряти відстані d₁ і d₂.

3. За формулою (5) обчислити g₁, результати внести в таблицю:

t1	T1	t2	T2	d1	d2	g1

Завдання 2.

1.Перемістити на стрижні один тягар так, щоб зменшити різницю періодів T₁, T₂ відхилити кінець маятника на 3-4 см., визначити час t₁ 10 коливань.

2. Перевертаючи маятник, зробити ті ж вимірювання, визначаючи t₂.

3. Переміщуючи тягарі і повторюючи дії пп.1-2, домогтися співпадання t₁і t₂.

4. Уточнити положення тягарів, зробивши вимірювання ста коливань. Домогтися відміни t₁і t₂ не більше ніж 1с.

5. Визначити середнє значення періоду коливань T = (t₁+ t₂ ) / 200.

6. За допомогою лінійки визначити відстань між призмами l - приведену довжину маятника.

7. За формулою (9) розрахувати g₂ і знайти різницю з результатом, одержаним в завданні 1 – Δg = g₂ – g₁:

Результати вимірів і розрахунків подати в таблиці:

t1	t2	T	l	g1	g2

Дайте відповіді на запитання:

1. Який з використаних методів є точнішим і більш раціональним?

2. Чому вказаними методами можна користуватися тільки при малих амплітудах коливань?

3. Чи залежить період коливань фізичного маятника від маси?

4. Як мають бути змінені вимірювання в другому завданні для збільшення точності визначення g?

Лабораторна робота № 13.

Вивчення стоячої хвилі в трубі.

Прилади та приладдя: установка, що складається з металічної труби з пересувним поршнем, камертон з відомою власною частотою коливань, вимірювальна лінійка, термометр.

Мета роботи: методом резонансу визначити довжину хвилі та швидкість її поширення в повітрі.

Коротка теорія та метод вимірювання

Звукові хвилі в повітрі являють собою послідовність згущень та розріджень повітря, що чергуються та поширюються з певною швидкістю, залежною від пружних властивостей середовища та його густини. Відстань між сусідніми згущеннями або розрідженнями називається довжиною хвилі. Звукові хвилі повздовжні, в них коливання частинок повітря здійснюється за напрямком поширення хвилі.

Так зване рівняння біжучої хвилі можна одержати у такий спосіб. Нехай на початку координат здійснюються гармонічні коливання з амплітудою A і циклічною частотою ω = 2πν (ν - кількість коливань за секунду або проста частота):

x = A sin (ωt). (1)

Нехай ці коливання передаються однорідному середовищу без втрат енергії, так що коливання поширюються в ньому з деякою сталою швидкістю v. Розглянемо деяку точку, що відстоїть від початку на відстані “у”. До цієї точки коливання дійдуть через проміжок часу Δt = y/v, що означає, що час коливань в точці, що розглядається, відстає від часу коливань на початку координат на Δt. Отже, точка “у” буде коливатися за законом

x₁ = A sin ω (t – y/v). (2)

Одержане рівняння біжучої хвилі - коливання довільної точки в довільний момент часу при відомому коливанні на початку координат.

Якщо хвиля розповсюджується вздовж труби і відбивається від поршня, то відбита хвиля буде описуватися рівнянням, що подібне (2), а тільки замість “у” слід писати “-у”:

x₂ = A sin ω (t + y/v). (3)

Складання прямої і відбитої хвиль призводить до такого коливання:

x = a sin ωt, де a = 2A cos (ωy / v), (4)

де а - амплітуда результуючого коливання в точці “у” залежить від її положення. Якщо зробити заміну за відомими співвідношеннями

ω = 2πν; v = λν, (5)

то для амплітуди результуючого коливання одержимо:

a = 2A cos (2πy / λ). (6)

При “у”, що дорівнює цілому числу півдовжин хвилі y = kλ/2 (k = 0,1,2, …), амплітуда коливань перетворюється в нуль.

Що ж являє собою коливання (4)? Ці коливання є такими, що зупинилися, бо фазовий множник sin (ωt) не містить координату “у”. Амплітуда цих коливань (6) в різних точках “у” різна. В тих місцях, де вона перетворюється в нуль, утворюються так звані вузли, а де амплітуда коливань максимальна - пучності. Коливання точок, що розміщені між сусідніми вузлами, відбуваються в одній фазі, що визначаються аргументом функції синус. Розподіл коливань в просторі нагадує, таким чином, хвилю, що зупинилася.

Якщо відбивання здійснюється від більш густого середовища, ніж те, в котрому поширюється пряма хвиля, то на місці відбивання завжди утворюється вузол. Отже, якщо вести відлік відстаней від поршня, то пучності відстоять від нього на відстанях:

l = (2k + 1) λ/4. (7)

Якщо поршень зміщений на відстань l (7) від обрізу труби, то в місці розміщення джерела звуку (на обрізу труби) виникне пучність. При цьому коливання джерела звуку (камертона), попадаючи в резонанс з коливаннями звукової хвилі, призводять до різкого підсилення гучності звуку. В цьому і полягає метод досліджень в даній роботі. Переміщуючи поршень, домагаються підсилення звуку і вимірюють послідовний ряд відстаней l₁, l₂, l₃, для яких справджується співвідношення (7). Складаючи значення l₁ + l₂ + l₃ = λ/4 + 3λ/4 + 5λ/4, визначають середнє значення довжини хвилі:

λ = 4 (l₁ + l₂ + l₃) / 9. (8)

За відомою частотою ν коливань камертона і знайденою λ знаходять швидкість звуку при даній температурі: v = λ/ν. Швидкість при t = 0 ˚С знаходить за відомою температурою залежністю:

v₀ = v / (9)

Порядок виконання роботи:

1. Повільно відсовують поршень від обрізу труби, безперервно постукуючи молоточком по камертону. При різкому підсиленні звуку підбирають положення поршня, переміщуючи його вперед і назад, що відповідає найбільшій гучності звуку, і вимірюють відстань l₁, від обрізу труби до поршня.

2. Переміщуючи поршень далі, повторюють дії пункту 1 і знаходять відстані l₁^’, l₂^’, l₃^’.

3. Двічі повторюють дії пп.1-2, вимірюючи l₁^”, l₂^”, l₃^”. Обчислюють середнє значення величини довжини l₁ = (l₁^’ + l₁^” + l₁^”’) /3 в кожній точці вимірювань.

4. За формулою (8) обчислюють λ, визначають v = λν і швидкість звуку при 0˚С за співвідношенням (9).

Результати вимірювань і розрахунків дати в таблиці:

ν	l1	l2	l3	λ	v	v0

У звіті подають повний розрахунок величин.

Дайте відповіді на запитання:

1. Як треба вести вимірювання, якщо камертон вііддалити від труби на деяку відстань b?

2. Як оцінити похибки вимірювань в цьому методі?

3. Як можна удосконалити метод вимірювань?

Лабораторная робота № 14.

Визначення показника адіабати повітря.

Прилади та приладдя: установка Клемана – Дезорма.

Коротка теорія та метод вимірювання

Адіабатичним називається процес, що протікає без теплообміну з навколишніми тілами. В газах адіабатичний процес можна здійснити при швидкому розширенні або стисканні газу. Проміжок часу стискання має бути такий, щоб не встиг відбутися теплообмін між газом і стінками посудини.

Адіабатичний процес описується рівнянням Пуаcсона:

p₁V₁^γ = p₂V₂^γ = const, (1)

де p - тиск, створюваний газом на стінки посудини об’ємом V. При цьому індекс “1” відноситься до одного стану газу, а індекс “2” - до іншого.

Графік процесу називається адіабатою, а величину γ показником адіабати. Вона дорівнює відношенню теплоємності газу при сталому тиску до теплоємності його при сталому об’ємі. В молекулярно-кінетичній теорії теплоємностей газу доводиться, що величина γ визначається числом ступенів вільності “і” молекули газу -

γ = (і +2) / і. (2)

В одноатомних молекул число ступенів вільності і=3, у лінійних молекул і=5, у нелінійних розгалуджених молекул і=6.

В даній роботі застосовується метод Клемана –Дезорма, в якому на основі здійснення адіабатичного процесу в газі визначається величина показника адіабати.

В балоні місткістю до 20 л знаходиться повітря при кімнатній температурі T₀ та атмосферному тиску P₀. За допомогою насоса тиск в балоні підвищують та надають газові час охолодитись до кімнатної температури. Маємо початковий стан газу, що характеризується тиском P₀ + H, об’ємом V₀ та температурою T₀. Відкриваємо кран, надаємо газові можливості розширитися та швидко закриваємо кран. Час розширення газу малий порівняно з часом теплообміну його з навколишнім середовищем. Процес можна вважати адіабатним. При адіабатному розширенні температура газу знижується до Т₁. Другий стан газу характеризується параметрами P₀, V₁ і T₁. Зв’язок параметрів газу в цих двох станах описується співвідношенням (1). Ми, на жаль, не знаємо ні об’єму V₁, ні температури T₁. Тому, застосувавши додатково до цих двох станів рівняння Менделеєва-Клапейрона, можна записати такі дві рівності:

(P₀ + H)V₀^γ = P₀V₁^γ, V₀^γ-1 = T₁V₁^γ-1 (3)

Після закриття крану в посудині виявилась інша маса газу, що характеризується атмосферним тиском P₀, об’ємом V₀ і температурою T₁. Якщо при закритому крані надати можливості газу нагрітися до кімнатної температури T₀, то при незмінному об’ємі V₀ тиск газу підійметься до P₀ + h.

Маємо зв’язок двох станів при ізохоричному процесі

P₀ / T₁ = (P₀ + h) / T₀ (4)

Із співвідношень (3) – (4) одержуємо рівність

(P₀ + h) / P₀ = T₀ / T₁ = (V₁ / V₀ )^{γ -1} = (P₀ + H) / P₀ )^{γ -1}

Розділимо почленно крайні члени останньої рівності

1+h / P₀ = (1 + H / P₀)^{γ -1}

і розкладемо праву частину рівності в ряд, приймаючи, що відношення h/P₀, а також H/P << 1. Тоді приходимо до рівняння

1 + h / P₀ = 1 + (γ – 1) (H / P₀),

або

γ = H / (H – h) (5)

Порядок виконання роботи:

1. Закрити випускний кран балона, обережно накачати насосом повітря, щоб різниця рівнів води в манометрі досягла 15-25 см. При накачуванні виконується робота стискування газу, тому температура його підіймається.

2. Зачекати 2-3 хв., доки температура в балоні зрівняється з кімнатною і перестануть змінюватися показання манометра. Відлічити показання різниці рівнів в манометрі H в міліметрах водяного стовпа.

3. Здійснити адіабатичний процес. Для цього швидко відкрити випускний кран і негайно закрити його, щойно зрівняються рівні води в манометрі. При цьому тиск в балоні дорівнюватиме атмосферному, температура буде нижчою за кімнатну.

4. Зачекати 2-3 хвилини до вирівнювання температури повітря в балоні з кімнатною. Це видно по затримці підвищення тиску в балоні. Записати різницю рівней в манометрі h в міліметрах водяного стовпа.

5. За формулою (5) обчислити показник адіабати.

Здійснити дії пунктів 1-5 ще 4 рази, змінюючи кожний раз тиск у вказаних межах.

Результати вимірювань та розрахунків занести до таблиці; знайти довірчий інтервал визначення показника адіабати для надійності 0,7:

№	H	h	γ	Δγ	γi =
					- - - - -
Середні значення

8. Беручі до уваги, що повітря складається в основному з двоатомних молекул азоту та кисню, для яких число ступенів вільності і=5, обчислити за (2) теоретичне значення показника адіабати.

Результати роботи подати у вигляді: γ = γ_ср. ± Δγ_ср.

Дайте відповіді на запитання:

1. Який процес називається адіабатичним і як здійснити цей процес?

2. Як змінюється температура системи при адіабатичному розширенні, стисканні?

3. В чому полягає причина різниці експериментально і теоретично знайденого значень показника адіабати?

4. Чому в даній роботі застосовують водяний, а не ртутний манометр?

Лабораторна робота № 15.

Дослідження вологості повітря.

Прилади та приладдя: психрометр Асмана, барометр-анероїд, таблиця тиску насиченої водяної пари (пружності водяної пари), психрометрична таблиця –номограма.

Мета роботи: засвоїти метод вимірювання вологості повітря.

Коротка теорія та метод вимірювань

Велика маса води на Землі призводить до того, що її атмосфера в значній мірі насичена водяною парою. Для багатьох цілей важливо знати кількість водяної пари, що міститься в атмосферному повітрі.

Одною з характеристик атмосфери є вологість повітря. Розрізняють абсолютну та відносну вологість.

Абсолютну вологість характеризують масою водяної пари, що міститься в 1 м³ повітря. Оскільки водяну пару в повітрі можна розглянути як своєрідну суміш газів, то до неї можна застосувати закон Дальтона: “Тиск суміші газів дорівнює сумі парціальних тисків компонентів”.

Парціальний тиск – це тиск, що створювався б одним компонентом при тій же температурі, що й суміш, якби він (даний компонент) займав весь об’єм, наданий суміші. Це вказує шлях для зведення характеристики абсолютної вологості як парціального тиску водяної пари.

При даній температурі є певна кількість пари, яка може міститься в одиниці об’єму, або інакше: при кожній температурі є гранично високий тиск пари. Пара при гранично високому при даній температурі тискові називається насиченою. Перевершення тиску насиченої пари у наявності центрів конденсаціі веде до конденсації лишків пари і пониження тиску до тиску насиченої пари. Тиск насиченої водяної пари при нормальному атмосферному тискові протабульований.

Абсолютна вологість не повністю характеризує стан атмосфери, бо одна і та ж кількість пари в одиниці об’єму при різних температурах по різному впливає на різні фізичні та інші процеси: пара, що ненасичена при високій температурі, стає насиченою при зниженні температури. В зв’язку з цим вводять ще одну характеристику – відносну вологість повітря як відношення тиску пари води, що міститься в повітрі при даних умовах, до тиску насиченої пари при тій же температурі (інколи – у відсотках).

B = (P / P_H) 100% (1)

Психрометр Асмана складається з двох термометрів, ртутний резервуар одного з яких обгорнуто батистом, змоченим у воді. Під час вимірювань термометри інтенсивно обдуваються повітрям за допомогою вентилятора. Внаслідок випаровування води, більшого відводу тепла від вологого термометра його температура Т_в встановлюється нижчою, ніж сухого Т_с.

Різниця температур Т_с - Т_в, що встановилася, свідчить про те, що кількість тепла Q, яке надходить з повітряного потоку, дорівнює кількості тепла Q_1, що витрачається на випаровування води. Згідно з законом Фур’є, кількість тепла, що надходить з повітряного потоку, можна подати як

Q = λ (Т_c – Т_в) S Δt, (2)

де λ - коефіцієнт теплопередачі від повітря до вологого термометра; S - площа поверхні термометра, що бере участь у теплообміні; Δt - деякий проміжок часу. Кількість тепла, що йде на випаровування, можна подати виразом

Q₁ = k l S (P_H^/ - P) Δt / H, (3)

де k - характеризує теплопередачу від балона термометра до вологого батисту; l - характеристика повітряного потоку; H - атмосферний тиск; P - тиск повітряної пари; P_H^/- тиск насиченої пари при температурі вологого термометра. Прирівнюючи Q і Q₁ і вводячи позначення A = λ / kl, одержуємо співвідношення для визначення тиску пари, що знаходиться в повітрі, тобто абсолютної вологості:

P = P_H^/ – AH (Т_c – Т_в). (4)

Сталу A визначають дослідним шляхом. Для психрометра Асмана в даній роботі A = 0,0005 К^-1.

Порядок виконання роботи:

1. Обережно зняти психрометр з зачіпки, ознайомитись з його конструкцією, впевнитись, що один з термометрів має батистову обгортку.

2. Наповнити водою ємність і вмочити кінець термометра обгорнутого батистом у воду.

3. Завести пружину вентилятора, обережно почепити психрометр на своє місце та спостерігати показання Т_c і вологого Т_в термометрів.

Дата добавления: 2015-05-24