Теоретичні відомості. Визначення логарифмічного декремента згасання коливань маятника

Визначення логарифмічного декремента згасання коливань маятника

Мета роботи: вивчення механічних згасаючих коливань.

Практично всяке коливання матеріальної точки, яке не підтримується ззовні, є згасаючим, амплітуда його з часом зменшується. Причина згасання полягає в наявності сил, що гальмують рух. Наприклад, це може бути сила тертя в точці підвісу при коливанні маятника, або сила опору середовища. Розглянемо випадок, коли тіло, масою 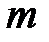, підвішене на пружині, здійснює прямолінійні коливання у в’язкому середовищі. Сила опору середовища залежить від швидкості руху тіла і за малих швидкостей її можна рахувати пропорційною швидкості, напрямлена вона в бік, протилежний швидкості. Позначимо коефіцієнт опору середовища через 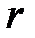, тоді другий закон Ньютона для даного випадку запишеться:

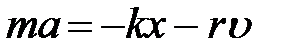, (1)

де 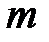‑ маса коливної точки, (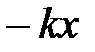) – пружна сила, яка є повертальною силою, 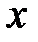‑ координати коливної точки, 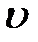‑ її швидкість. Введемо позначення:

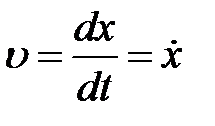‑ перша похідна від 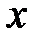по часу,

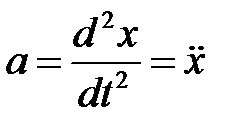‑ друга похідна від 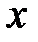по часу.

Запишемо рівняння (1) у вигляді

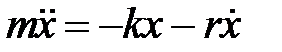. (2)

Поділивши праву і ліву частини цього рівняння на 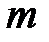, одержимо:

. (3)

Введемо позначення:

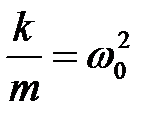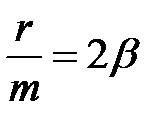, , (4)

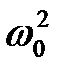де і 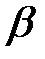‑ додатні.

Тоді рівняння (3) набуде вигляду:

. (5)

Введемо нову змінну , що пов’язана з 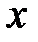співвідношенням

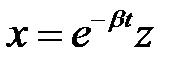. (6)

Тоді перша похідна виразу (6) 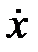запишеться:

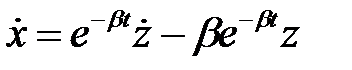, (7)

а друга похідна 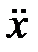буде:

. (8)

Підставивши значення 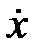та у рівняння (5), одержимо (скоротивши всі члени на множник ):

,

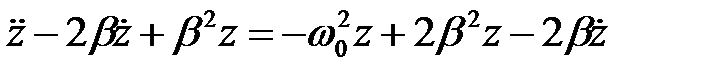або

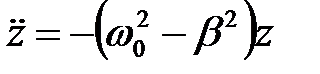. (9)

Якщо опір середовища малий, , то ‑величина додатна і можна ввести позначення:

, (10)

після чого рівняння (9) матиме вигляд:

. (11)

І розв'язок його можна записати у вигляді (оскільки це фактично є диференціальне рівняння гармонічних коливань):

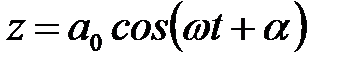. (12)

Отже, величина 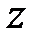змінюється періодично, з періодом

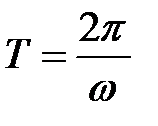, (13)

або, підставляючи замість його значення з (10):

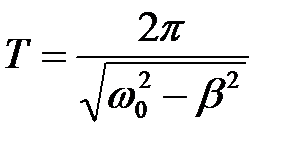, (14)

або, скориставшись виразом (4):

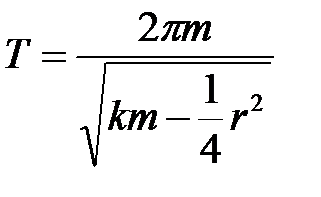. (15)

Підставивши в рівняння (6) замість його значення з формули (12), одержимо закон руху точки під дією пружної сили в середовищі з опором:

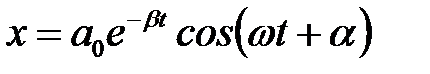, (16)

де 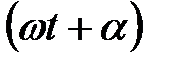‑ фаза коливань, 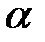‑ початкова фаза, 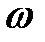‑ кругова частота, 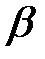‑ коефіцієнт згасання, який можна записати також у вигляді:

. (17)

Цей розв'язок представляє собою коливання з амплітудою 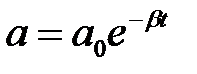, щозменшується з часом. Період коливання 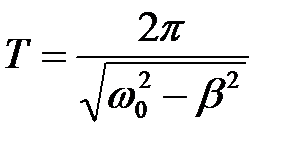в середовищі з опором більший, ніж період коливань точки такої ж маси 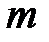під дією пружної сили в середовищі без опору. Графік залежності від часу подано на рис. 1. Як бачимо, коливання згасають з часом.

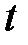
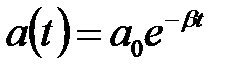
Рис. 1. Графік згасаючих коливань.

Логарифм відношення двох послідовних амплітуд,що віддалені в часі одна від одної на проміжок часу, що дорівнює періоду 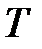,називається логарифмічним декрементом згасання. Позначимо логарифмічний декремент літерою 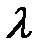і запишемо за визначенням:

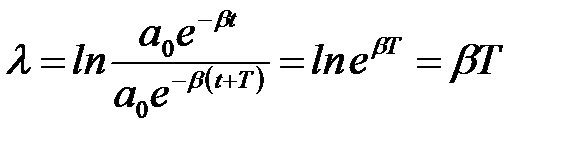або . (18)

Відношення послідовних амплітуд називається декрементом згасання:

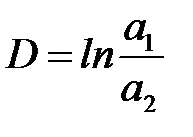. (19)

Логарифмічний декремент можна визначити безпосередньо із співвідношень, вимірявши значення амплітуд 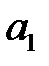та 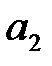двох послідовних коливань:

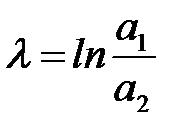. (20)

Знаючи , можна визначити коефіцієнт опору середовища :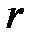

. (21)

Отже, енергія, що надана системі при виведенні її з положення рівноваги, за наявності згасань поступово витрачається на роботу проти сил тертя, і, щоб підтримати коливання незгасаючими, до системи необхідно підводити енергію ззовні.

Прикладом системи, коливання якої, незважаючи на наявність сил тертя, відбувається завдяки енергії, що підводиться, із незмінною амплітудою, може слугуватигодинниковий маятник. Храповий механізм підштовхує маятник у такт з його коливаннями. Енергія, що передається при цьому маятнику, береться або за рахунок пружин, що розкручуються, або за рахунок вантажу, що опускається. Така система, що підтримує незмінною амплітуду своїх коливань, називається автоколивною системою.

На практиці для визначення коефіцієнта затухання ведуть спостереження за згасаючими коливаннями за проміжок часу 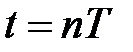, що дорівнює цілому числу періодів коливань.

Амплітуда згасаючих коливань визначається за формулою

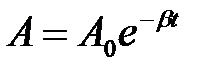, (22)

де ‑ амплітуда, що визначається енергією системи в момент часу 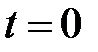. Коефіцієнт згасання визначається з виразу

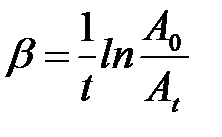. (23)

І, таким чином, визначаємо зменшення амплітуди за одиницю часу. Якщо 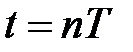, то вираз (23) матиме вигляд:

, (24)

де 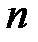‑ число коливань. При значних згасаннях зручно вибрати 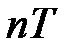таким, щоб початкова амплітуда зменшувалась у ціле число разів, наприклад, у два рази. Тоді:

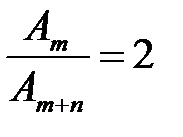, . (25)

Дата добавления: 2015-05-24