Влияние параметров модели термоциклической прочности на запас по числу циклов

Запас по числу циклов нагревов (формула (58)) зависит от ряда параметров:

каждый из которых известен при разработке конструкции с определенной точностью.

Оценим относительное влияние параметров. Рассмотрим сначала вопрос в общем виде, предполагая, что имеется функция параметров х и у следующего вида:

Тогда по правилу дифференцирования функции многих переменных

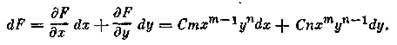
Разделив обе части равенства на F, найдем

Для малых относительных приращений

Последнее соотношение имеет четкий физический смысл: 1% отклонения параметра х дает m% отклонения величины F; 1% отклонения параметра у дает n % указанного отклонения.

Применяя этот прием для анализа зависимости (58), находим

Знак минус перед отдельными слагаемыми означает, что приращение параметра вызывает уменьшение запаса числа циклов п_а.

С помощью зависимости (63) устанавливаем, например, что погрешность в определении температуры нагрева на 1% вызывает погрешность 8,3% запаса по долговечности.

Учет ползучести материала при определении температурных напряжений. На рис. 6.14 показано изменение температурных напряжений при циклическом изменении температуры без учета ползучести материала. Рассмотрим теперь влияние ползучести на температурные напряжения в стержне с заделанными концевыми сечениями (см. рис. 6.13).

Будем считать в начальный момент времени

Далее следует учесть, что в любой момент времени сумма упругой деформации ε_e(t), деформации ползучести ε_c(t) и температурной деформации справедливо уравнение

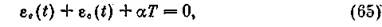
гак как расстояние между заделками и температура не изменяются. Упругая деформация

Дифференцируя по времени зависимость (65) и учитывая, что температура после нагрева остается постоянной, находим

Пренебрегая неустановившейся стадией ползучести, примем для скорости ползучести степенную зависимость (см. разд. 20)

где В, п — параметры материала.

Теперь из соотношения (67) получаем

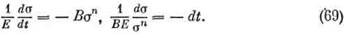
Интегрируя в. пределах от 0 до t, найдем

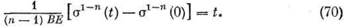
Учитывая, что в практических случаях п > 1, запишем послед­нее равенство так:

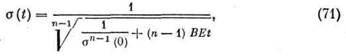или

где а = (п — 1)BEσ^n-1 (0). Значение σ(0) определяется равенством (64),

С увеличением времени t абсолютная величина температурного напряжения в результате влияния ползучести падает. Этот процесс называется релаксацией температурных напряжений.

Деформация ползучести представляет собой остаточную деформацию. Из уравнения (65) можно получить

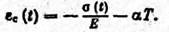
Если в момент времени t снять нагрев, то в стержне возникает остаточное напряжение растяжения

так как длина стержня должна оставаться неизменной, аматериал стержня в результате ползучести получил остаточную деформацию сжатия ε _е(t) В силу образования остаточных деформаций ползучести температурные напряжения сжатия в момент нагрева все время падают, а в период останова в стержне появляются растягивающие остаточные напряжения.

Дата добавления: 2015-05-08