Модель с установленной периодичностью пополнения запаса до постоянного уровня

Эта модель объединяет принципы управления запасами для двух предыдущих систем.

Заказ делается через равные промежутки времени, однако в том случае, если фактический остаток на складе снизится до уровня второго бункера, т.е. станет равен Q₂ то делается внеочередной заказ. Размер заказа равен разности между максимальным заказом и фактическим наличием запаса на момент заказа, т.е.

qз= Qmax-Qфакт

или между максимальным запасом и запасом в точке заказа, т.е.

qз= Qmax-Qз

Рис. 9. График пополнения и расходования запаса в системе с постоянной периодичностью

Графически этот случай изображен на рис. 10.

Управляющими параметрами, которые здесь нужно определить, являются период между двумя смежными заказами и максималь­ный размер запаса. Все эти параметры будут постоянными, а объем заказа — переменной величиной.

Применение системы целесообразно при значительных измене­ниях в потребности МР, ГП (колебаниях расхода) и необходимос­ти исключить возможность их нехватки до наступления срока оче­редной поставки. Реализация этой модели требует оперативного (ежедневного) контроля наличия запасов на складе.

Все системы пополнения запасов связаны с определенным по­рядком контроля их фактического уровня на складах, что часто требует затрат финансовых, трудовых и информационных ресур­сов, особенно для многономенклатурных (многоассортиментных) запасов. Однако обычно из общего числа наименований наиболь­шая стоимость запаса (или основная доля затрат на управление ими) падает на относительно небольшое их количество.

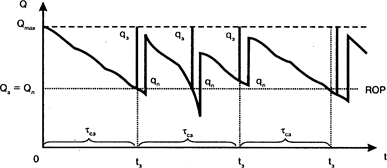
Рис. 10. График пополнения и расходования запаса в системе с установленной периодичностью пополнения запаса до постоянного уровня

ГЛАВА 4. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ

Чрезвычайно трудно построить обобщенную модель управления запасами, которая учитывала бы все разновидности условий, наблюдаемых в реальных системах. Но если бы и удалось построить достаточно универсальную модель, она едва ли оказалась аналитически разрешимой[7]. Представление в этом разделе модели соответствуют некоторым системам запасами. Маловероятно, что эти модели могут точно подойти для реальных условий, однако они приведены с целью различных подходов к решению некоторых конкретных задач управления запасами.

Дата добавления: 2015-05-08