Тригонометрия в астрономии

Применение тригонометрии в физике и ее задачах

Практическое применение тригонометрических уравнений в реальной жизни

Существует множество областей, в которых применяются тригонометрия. Например, метод триангуляции используется в астрономии для измерения расстояния до ближайших звезд, в географии для измерения расстояний между объектами, а также в спутниковые навигационных системах. Синус и косинус имеют фундаментальное значение для теории периодических функций, например при описании звуковых и световых волн.

Тригонометрия используются в астрономии (особенно для расчётов положения небесных объектов, когда требуется сферическая тригонометрия), в морской и воздушной навигации, в теории музыки, в акустике, в оптике, в анализе финансовых рынков, в электронике, в теории вероятностей, в статистике, в биологии, в медицинской визуализации (например, компьютерная томография и ультразвук), в аптеках, в химии, в теории чисел, в метеорологии, в океанографии, во многих физических науках, в межевании и геодезии, в архитектуре, в фонетике, в экономике, в электротехнике, в машиностроении, в гражданском строительстве, в компьютерной графике, в картографии, в кристаллографии, в разработке игр и многих других областях.

В окружающем нас мире приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Эти процессы называются колебательными. Колебательные явления различной физической природы подчиняются общим закономерностям и описываются одинаковыми уравнениями. Существуют разные виды колебательных явлений.

Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом:

Где х — значение изменяющейся величины, t — время, А — амплитуда колебаний, ω — циклическая частота колебаний, — полная фаза колебаний, r — начальная фаза колебаний.

Обобщенное гармоническое колебание в дифференциальном виде x’’ + ω²x = 0.

Задача:

Камень брошен на склоне горы под углом α к ее поверхности. Определите дальность полета камня, если начальная скорость камня равна v₀, угол наклона горы к горизонту β. Сопротивление воздуха не учитывать.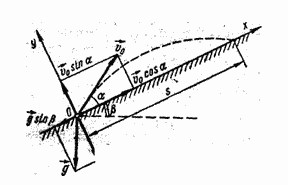

Решение. Сложное движение камня по параболе нужно представить как результат наложения двух прямолинейных движений: одного вдоль поверхности Земли, другого - по нормали к ней.

Выберем прямоугольную систему координат с началом отсчета в точке бросания камня так, чтобы оси OX и OY совпали с указанными направлениями, и найдем составляющие векторов начальной скорости v₀ и ускорения свободного падения g по осям. Проекции этих составляющих на оси OX и OY равны соответственно:
v₀cosα v₀; -g sinβ -g cosβ

После этого сложное движение можно рассматривать как два более простых: равнозамедленное движение вдоль поверхности Земли с ускорением g sinβ и равнопеременное движение, перпендикулярное склону горы, с ускорением g cosβ.

Составляем уравнения движения для каждого направления с учетом того, что за время t всего движения перемещение камня по нормали к поверхности (по оси OY) оказалось равным нулю, а вдоль поверхности (по оси OX) - равным s:

(1)

0= v0sinα t1-g cosβ t²1/2

(2)

s= v0cosα t1-g sinβ t²1/2

По условию задачи v₀,α и β нам заданы, поэтому в составленных уравнениях имеется две неизвестные величины s и t1.

Из первого уравнения определяем время полета камня:

t₁=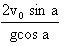

Подставляя это выражение во второе уравнение, находим:

S= v₀cosα∙ =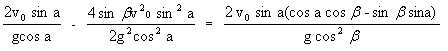
=

Анализируя решение приведенной задачи, можно сделать вывод, что математика имеет аппарат и использование его при реализации меж предметной связи физики и математики ведет к осознанию единства мира и интеграции научных знаний.

Математика выступает как своеобразный язык, необходимый для кодирования содержательной физической информации.

Использование меж предметной связи физики и математики ведет к сравниванию этих двух наук и позволяет усиливать качественную теоретическую и практическую подготовку обучаемых.

Потребность в решении треугольников раньше всего обнаружилась в астрономии; поэтому, в течение долгого времени тригонометрия развивалась и изучалась как один из разделов астрономии.

Потребность в решении треугольников раньше всего обнаружилась в астрономии; поэтому, в течение долгого времени тригонометрия развивалась и изучалась как один из разделов астрономии.

Составленные Гиппархом таблицы положений Солнца и Луны позволили предвычислять моменты наступления затмений (с ошибкой 1—2 ч). Гиппарх впервые стал использовать в астрономии методы сферической тригонометрии. Он повысил точность наблюдений, применив для наведения на светило крест нитей в угломерных инструментах — секстантах и квадрантах. Ученый составил огромный по тем временам каталог положений 850 звезд, разделив их по блеску на 6 степеней (звездных величин). Гиппарх ввел географические координаты — широту и долготу, и его можно считать основателем математической географии. (ок. 190 до н. э. — ок. 120 до н. э.)

Дата добавления: 2015-05-08