Автоматы Мили и Мура 1 страница

Абстрактные автоматы

1.1. Определение абстрактного автомата
1.2. Методы задания автоматов
1.2.1. Табличный
1.2.2. Графический
1.2.3. Матричный
1.3. Связь между моделями Мили и Мура
1.3.1. Реакция А Мили
1.3.2. Реакция А Мура
1.3.3. Пример
1.3.4. Переход от А Мура к А Мили
1.3.5. Переход от А Мили к А Мура
1.3.6. Пример преобразования автомата Мили в автомат Мура
1.3.7. Пример перехода от автомата Мили с переходящим состоянием к автомату Мура
1.4. Минимизация полностью определенных автоматов
1.4.1. Теоретические основы минимизации
1.4.2. Алгоритм минимизации
1.4.3. Пример минимизации автомата Мили
1.4.4. Пример минимизации автомата Мура
1.5. Совмещенная модель автомата (С-автомат)

1.1. Определение абстрактного автомата

Математической моделью дискретного управляющего устройства является абстрактный автомат, который задается множеством из шести Элементов: S = {A, Z, W, , , а1}, где
А = {а₁,..., а_m,..., а_M} - множество состояний (алфавит¹ состояний);
Z = {z₁,..., z_f,..., z_F} - множество входных сигналов (входной алфавит);
W = {w₁,..., w_g,..., w_G} - множество выходных сигналов (выходной алфавит);
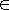- функция переходов, реализующая отображение множества D А x Z в А (а_s = (а_m, z_f), а_s А);
- функция выходов, реализующая отображение множества D А x Z на W (w_g = (а_m, z_f ));
а₁ 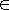А - начальное состояние автомата.
Автомат² называется конечным, если конечны множества А, Z, W. В дальнейшем будут рассматриваться только конечные автоматы и термин <конечный> почти всегда будет опускаться. Автомат называется полностью определенным, если D_б = D_л = А x Z. Иными словами, у полностью определенного автомата области определения функции и совпадают со множеством А x Z - множеством всевозможных: пар вида (a_m, z_f ). У частичного автомата функции или определены не для всех пар (а_m, z_f) 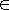А x Z.
Понятие состояния в определение автомата введено в связи с тем, что: возникает необходимость в описании поведения систем, выходы которых зависят не только от состояния входов в данный момент времени, но от некоторой предыстории, т. е. от сигналов, которые поступали на входы системы ранее. Состояния как раз и соответствуют некоторой памяти о прошлом позволяя устранить время как явную переменную и выразить выходные сигналы, как функцию состояний и входов в данный момент времени.
Абстрактный автомат (рис. 1-1) имеет один входной и один выходной канал. В каждый момент t = 0, 1, 2,... дискретного времени автомат находится в определенном состоянии a (t) из множества А состояний автомата, причем в начальный момент t= 0 он всегда находится в начальном состоянии а (0) = а1. В момент t, будучи в состоянии a (t), автомат способен воспринять на входном канале сигнал z (t) 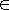Z и выдать на выходном канале сигнал w (t) = (а (t), z (t)), переходя в состояние а (t + 1) = (а (t), z(t)); а(t) А, w(t) W. Смысл понятия абстрактного автомата состоит в том, что он реализует некоторое отображение множества слов входного алфавита Z во множество слов выходного алфавита W. Другими словами, если на вход автомата, установленного в начальное состояние а1, подавать буква за буквой некоторую последовательность букв входного алфавита z(0), z(1), z(2),... -входное слово, то на выходе автомата будут последовательно появляться буквы выходного алфавита w(0), w(1), w(2),... - выходное слово. Относя к каждому входному слову соответствующее ему выходное слово, мы получим отображение , индуцированное абстрактным автоматом.

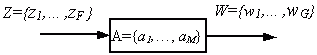
Рис. 1-1. Абстрактный автомат

На практике наибольшее распространение получили автоматы Мили и Мура Закон функционирования автомата Мили задается уравнениями

a(t+1) = (а(t), z(t)); w(t)= (a(t), z(t)), t = 0,1,2,... (1-1)

а закон функционирования автомата Мура - уравнениями

a(t+1) = (а(t), z(t)); w(t)= (a(t)), t = 0,1,2,...

¹ Всякий конечный набор попарно различных символов можно рассматривать как некоторый алфавит, буквы которого - указанные символы Конечную упорядоченную последовательность букв назовем словом в данном алфавите.
² До главы 2 под термином <автомат> понимается абстрактный автомат.

1.2. Методы задания автоматов

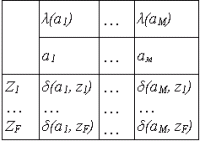
Чтобы задать конечный автомат S, необходимо описать все элементы множества S = {A, Z, W, , , а1}, т. е. входной и выходной алфавиты и алфавит состояний, а также функции переходов и выходов. Среди множества состояний необходимо выделить состояние a1, в котором автомат находится в момент t = 0. Существует несколько способов задания работы автомата, но наиболее часто используются табличный, графический и матричный.

1.2.1. Табличный

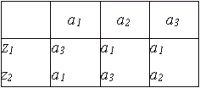
Описание работы автомата Мили таблицами переходов и выходов иллюстрируется таблицами 1-1 и 1-2. Строки этих таблиц соответствуют входным сигналам, а столбцы - состояниям, причем крайний левый столбец состояний обозначен начальным состоянием а1.

Т 1-1 Общий вид таблицы переходов автомата Мили	Т 1-2 Общий вид таблицы выходов автомата Мили

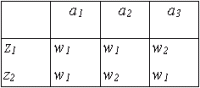
На пересечении столбца а_m и строки z_f в таблице переходов ставится состояние а_s = (а_m, z_f), в которое автомат переходит из состояния аm под действием сигнала z_f, а в таблице выходов-соответствующий этому переходу выходной сигнал w_g = (а_m, z_f). Пример табличного способа задания полностью определенного автомата Мили S₁ с тремя состояниями, двумя входными и двумя выходными сигналами приведен в таблицах 1-3 и 1-4.

Т 1-3 Таблица переходов автомата Мили S1	Т 1-4 Таблица выходов автомата Мили S1

Для частичных автоматов, у которых функции или определены не для всех пар (а_m, z_f) А х Z, на месте неопределенных состояний и выходных сигналов ставится прочерк (частичный автомат S₂ задан таблицами 1-5 и 1-6).

Т 1-5 Таблица переходов частичного автомата Мили S2	Т 1-6 Таблица выходов частичного автомата Мили S2

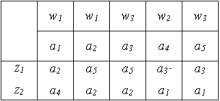
Т 1-7 Общий вид отмеченной таблицы переходов автомата Мура	Т 1-8 Отмеченная таблица.переходов автомата Мура S2

Так как в автомате Мура выходной сигнал зависит, только от состояния, автомат Мура задается одной отмеченной таблицей переходов (таблица 1-7), в которой каждому ее столбцу приписан, кроме состояния а_m, еще и выходной сигнал w_g = (а_m), соответствующий этому состоянию. Пример табличного описания автомата Мура S₃ иллюстрируется таблицей 1-8.

1.2.2. Графический

Граф автомата - ориентированный связный граф, вершины которого соответствуют состояниям, а дуги - переходам между ними.

рис. 1-2 Граф автомата Мили S1	рис. 1-3 Граф автомата Мили S2

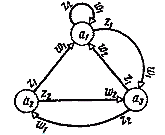
Две вершины графа автомата а_m и а_s (исходное состояние и состояние перехода) соединяются дугой, направленной от а_m к а_s, если в автомате имеется переход из а_m в а_s, т. е. если а_s = (а_m, z_f) при некотором z_f 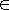Z. Дуге (а_m, а_s) графа автомата приписывается входной сигнал z_f и выходной сигнал w_g = (а_m, z_f), если он определен, и ставится прочерк в противном случае. Если переход автомата из состояния а_m в состояние а _s происходит под действием нескольких входных сигналов, то дуге (а_m а_s) приписываются все эти входные и соответствующие выходные сигналы. При описании автомата Мура в виде графа выходной сигнал w_g = (а_m) записывается внутри вершины или рядом с ней. На рис.1-2, 1-3 и 1-4 приведены заданные ранее таблицами графы автоматов S₁, S₂, S₃.

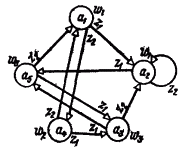
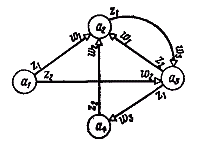
Рис. 1-4. Граф автомата Мили S₃

1.2.3. Матричный

Матрица соединений автомата есть квадратная матрица 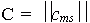, строки которой соответствуют исходным состояниям, а столбцы - состояниям перехода. Элемент с_ms= z_f / w_g, стоящий на пересечении m -ой строки и s -го, в случае автомата Мили соответствует входному сигналу z_f, вызывающему переход из состояния а_m в состояние а_m, и выходному сигналу w_g, выдаваемому на этом переходе. Для автомата Мили S₁ матрица C₁ имеет вид

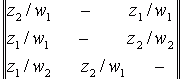
Если переход из а_m в а_s происходит под действием нескольких сигналов, элемент сms представляет собой множество пар (вход/выход) для этого перехода, соединенных знаком дизъюнкции. Для модели Мура элемент c_ms равен множеству входных сигналов на переходе (а_m, а_s) а выход описывается вектором выходов

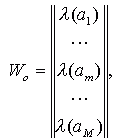
m -я компонента которого есть выходной сигнал, отмечающий состояние а_m. Для автомата Мура S₃

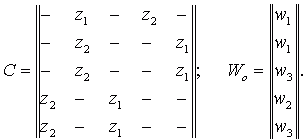
В данной работе рассматриваются только детерминированные автоматы, у которых выполнено условие однозначности переходов: автомат, находящийся в некотором состоянии, под действием любого входного сигнала не может перейти более чем в одно состояние. Применительно к графическому способу задания автомата это означает, что в графе автомата из любой вершины не могут выходить две и более дуги, отмеченные одним и тем же входным сигналом. Аналогично этому в матрице соединений автомата в каждой строке любой входной сигнал не должен встречаться более одного раза.

Т 1-9 Отмеченная таблица переходов асинхронного автомата Мура S ₄

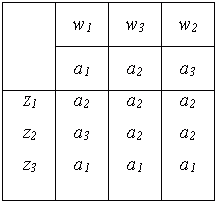
В заключение данного параграфа определим синхронные и асинхронные автоматы. Состояние а_s автомата S называется устойчивым состоянием, если для любого входа z_f Z, такого, что (а_m, z_f) = а_s, имеет место (а_s, z_f) = а_s.

Автомат S называется асинхронным, если каждое его состояние a_s A устойчиво. Автомат S называется синхронным, если он не является асинхронным. Необходимо заметить, что построенные на практике автоматы - всегда асинхронные и устойчивость их состоянии всегда обеспечивается тем или иным способом, например введением сигналов синхронизации (см. ниже, § 3-1).

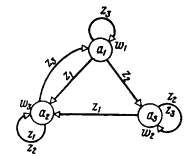
Рис. 1-5. Граф асинхронного автомата Мура S₄

Однако на уровне абстрактной теории, когда автомат есть лишь математическая модель, которая не отражает многих конкретных особенностей его возможной реализации, часто оказывается более удобным оперировать с синхронными автоматами, что мы и будем делать на протяжении всей данной главы. Пример асинхронного автомата Мура S ₄ приведен в табл. 1-9 и на рис. 1-5 Нетрудно видеть, что все его состояния устойчивы.

Очевидно, что если в таблице переходов асинхронного автомата некоторое состояние а_s стоит на пересечении строки z_f и столбца а_m (m<>s), то это состояние а_s обязательно должно встретиться в этой же строке в столбце а_s. В графе асинхронного автомата, если в некоторое состояние имеются переходы из других состояний под действием каких-то сигналов, то в вершине a_s, должна быть петля, отмеченная символами тех же входных сигналов. Анализ таблиц 1-3, 1-5 и 1-8 или рис. 1-2 - 1-4 показывает, что автоматы S₁, S₂ и S₃ являются синхронными.

1.3. Связь между моделями Мили и Мура

1.3.1. Реакция А Мили

В § 1-1 отмечалось, что абстрактный автомат работает как преобразователь слов входного алфавита в слова в выходном алфавите. Остановимся на этом вопросе более подробно, взяв в качестве примера автомат Мили S₁ на рис. 1-2 (или табл. 1-3, 1-4). Пусть на вход этого автомата, установленного в начальное состояние, поступает входное слово 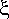= z₁z₁z₂z₁z₂ z₂. Так как (a₁,z₁)=a₃, а (a₁,z₁)=w₁,то под действием первой буквы слова 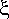- входного сигнала z₁ автомат перейдет в состояние а₃ и на выходе его появится сигнал w₁. Далее, (a₃,z₁)=a₁, (a₃,z₁)=w ₂ и потому при приходе второго сигнала z₁ автомат окажется в состоянии a₁, а на выходе его появится сигнал w₂. Проследив непосредственно по графу или таблицам переходов и выходов дальнейшее поведение автомата, опишем его тремя строчками, первая из которых соответствует входному слову 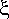вторая - последовательности состояний, которые проходит автомат под действием букв слова 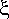, третья - выходному слову W, которое появляется на выходе автомата:

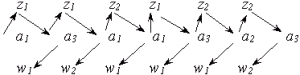
Назовем W = (а₁, 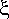) реакцией автомата Мили в состоянии а₁ на входное слово 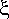. Как видно из примера, в ответ на входное слово длины k автомат Мили выдает последовательность состояний длины k+1 и выходное слово длины k. В общем виде поведение автомата установленного в состояние а_m, можно описать следующим образом:

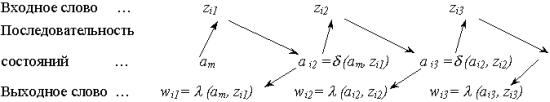
1.3.2. Реакция А Мура

Точно так же можно описать поведение автомата Мура, находящегося в состоянии а_m, при приходе входного слова z_i1,z_i2,:,z_ik. Напомним, что в соответствии с (1-2) выходной сигнал в автомате Мура в момент времени t(w(t)) зависит лишь от состояния, в котором находится автомат в момент t(а(t)):

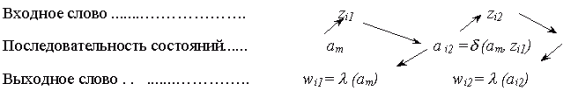
Продолжение

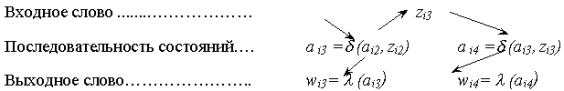
Очевидно, что выходной сигнал w_i1= (а_m) в момент времени i₁ не зависит от входного сигнала z_i1, а определяется только состоянием а _m. Таким образом, этот сигнал w₁ никак не связан с входным словом, поступающим на вход автомата, начиная с момента i₁. В связи с этим под реакцией автомата Мура, установленного в состояние а_m, на вход-слово 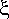=z_i1z_i2:z_ik будем понимать выходное слово той же длины W = (а_m, 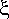)=w_i2w_i3:w_ik+1.

1.3.3. Пример

В качестве примера рассмотрим автомат Мура S₅, граф которого изображен на рис. 1-6 и найдем его реакцию в начальном состоянии a₁ на то же самое входное слово 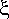= z₁z₁z₂z₁z₂z₂, которое мы использовали при анализе поведения автомата Мили S₁:

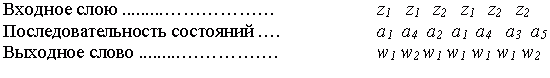
Как видно из этого и предыдущего примеров, реакции автоматов S₅ и S₁ в начальном состоянии на входное слово 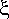с точностью до сдвига на 1 такт совпадают. Дадим теперь строгое определение эквивалентности полностью определенных автоматов.
Два автомата S_A и S_B с одинаковыми входными и выходными алфавитами называются эквивалентными, если после установления их в начальные состояния их реакции на любое входное слово совпадают.

1.3.4. Переход от А Мура к А Мили

Можно показать [7], что для любого автомата Мили существует эквивалентный ему автомат Мура и, обратно, для любого автомата Мура существует эквивалентный ему автомат Мили. При описании алгоритмов взаимной трансформации автоматов Мили и Мура в соответствии с изложенным выше мы будем пренебрегать в автоматах Мура выходным сигналом, связанным с начальным состоянием (a₁).
Рассмотрим сначала преобразование автомата Мура в автомат Мили. Пусть дан автомат Мура

S_A={A_A, Z_A, W_A, _A, _A, a_1A},

где

A_A = {а₁,:, а_m,:, a_M},
Z_A= {z₁,:, z_f,:, z_F},
W_A = {w₁,:, w_g,:, w_G};

_A - реализует отображение A_A х Z _A в A_A, _A - отображение A _A на W_A, а a_1A = a₁ - начальное состояние.

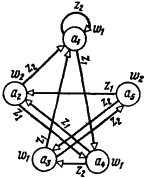
Рис. 1-6. Граф автомата Мура S₅

Рис. 1-7. Иллюстрация перехода от модели Мура к модели Мили

Построим автомат Мили

S_B={A_B, Z_B, W_B, _B , _B, a_1B},

у которого

A_B = A_A = {а₁,:, а_m,:, a_M},
Z_B= Z_A = {z₁,:, z_f,:, z_F},
W_B = W_A = {w₁,:, w_g,:, w_G};
_B = _A, a_1B = a _1A = a₁

Функцию выходов Мили _B определим следующим образом. Если в автомате Мура _A(a_m,z_f)=a_s и _A(a_s)=w_g, то в автомате Мили _B(a_m,z_f)=w_g.
Переход от автомата Мура к автомату Мили при графическом способе задания иллюстрируется рис.1-7: выходной сигнал (w_g), записанный рядом с вершиной (а_s), переносится на все дуги, входящие в эту вершину. На рис. 1-8 приведен граф автомата Мили S₆, эквивалентного автомату Мура S₃ (рис. 1-4).
При табличном способе задания автомата S_A таблица переходов автомата S_B совпадает с таблицей переходов S_A, а таблица выходов S_B получается из таблицы переходов заменой символа a_s, стоящего на пересечении строки z_f и столбца a_m, символом выходного сигнала w_g, отмечающего столбец a_s , в таблице переходов автомата S_A.
Из самого способа построения автомата Мили S_B очевидно, что он эквивалентен автомату Мура S_A. Действительно, если некоторый водной сигнал z_f 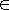Z поступает на вход автомата S_A, находящегося в состоянии а_m, то он перейдет в состояние а_s= _A(а_m,z_f) и выдаст входной сигнал w_g= _A(а_s). Но соответствующий автомат Мили S_B из состояния a_m, также перейдет в состояние a_s, поскольку _B(а_m,z_f) = _A(а_m,z_f) = а_s - и выдаст тот же выходной сигнал w_g согласно способу построения функции _В. Таким образом, для входной последовательности длины один поведение автоматов S_A и S_B полностью совпадает. По индукции нетрудно показать, что любое входное слово конечной длины, поданное на входы автоматов S_A и S_B , установленных в состояния a_m, вызовет появление одинаковых выходных слов и, следовательно, автоматы S_A и S_A а_m эквивалентны.

Дата добавления: 2015-05-09