
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Автоматы Мили и Мура 2 страница
|
|
|
|
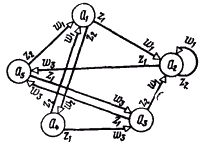
Рис. 1-8. Автомат Мили S6эквивалентный автомату Мура S5
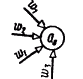
Рис. 1-9. Построение множества As
1.3.5. Переход от А Мили к А Мура 
Прежде чем рассмотреть трансформацию автомата-Мили в автомат Мура, наложим на автомат Мили следующее ограничение: у автомата не должно быть преходящих состояний. Под преходящим будем понимать состояние, в которое при представлении автомата в виде графа не входит ни одна дуга, но которое имеет по крайней мере одну выходящую дугу (пример - состояние a1 на рис. 1-3). Итак, пусть задан автомат Мили
SA={AA, ZA, WA,  A,
A,  A, a1A},
A, a1A},
где
AA = {а1,:, аm,:, aM},
ZA= {z1,:, zf,:, zF},
WA = {w1,:, wg,:, wG};
 A - реализует отображение AA х ZA в AA,
A - реализует отображение AA х ZA в AA,  A - отображение AA на WA , а a1A = a1 - начальное состояние.
A - отображение AA на WA , а a1A = a1 - начальное состояние.
Построим автомат Мура
SB={AB, ZB, WB,  B,
B,  B, a1B},
B, a1B},
у которого
ZB= ZA = {z1,:, zf,:, zF},
WB = WA = {w1,:, wg,:, wG};
Для определения АB каждому состоянию as 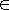 AA поставим в соответствие множество As всевозможных пар вида (аs,w g), где wg - выходной сигнал, приписанный входящей в аs дуге (рис. 1-9): Аs={(as, wg) |
AA поставим в соответствие множество As всевозможных пар вида (аs,w g), где wg - выходной сигнал, приписанный входящей в аs дуге (рис. 1-9): Аs={(as, wg) |  (am, zf) = as и
(am, zf) = as и  (am, zf) = wg}
(am, zf) = wg}
Число элементов в множестве Аs равно числу различных выходных сигналов на дугах автомата S A, входящих в состояние as.
Множество остояний автомата SB получим как обединение множеств AS (s=1,:,M):
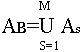
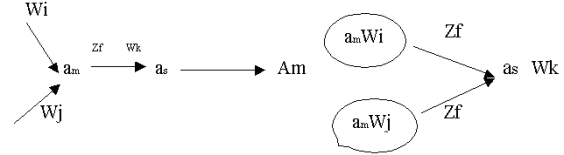
Рис. 1-10. Иллюстрация перехода от модели Мили к модели Мура
Функции выходов  B и переходов
B и переходов  B определим слудиющим образом. Каждому состоянию автомата Мура SB, представляющему собой пару вида (as, Wg), поставим в соответствие выходной сигнал Wg. Если в автомате Мили SA был переход а1B (аm, zf) = Wk , то в SB (рис. 1-10) будет переход из множества состояний Am, порождаемых am, в состояние (as, Wk) под действием входного сигнала zf.
B определим слудиющим образом. Каждому состоянию автомата Мура SB, представляющему собой пару вида (as, Wg), поставим в соответствие выходной сигнал Wg. Если в автомате Мили SA был переход а1B (аm, zf) = Wk , то в SB (рис. 1-10) будет переход из множества состояний Am, порождаемых am, в состояние (as, Wk) под действием входного сигнала zf.
В качестве начального состояния а1B можно взять любое из состояний множества А1, которое порождается начальным состоянием а1 автомата SA. Напомним, что при сравнении реакции автоматов SA и SB на всевозможные входные слова не должен учитываться выходной сигнал в момент времени t=0, связанный с состоянием а1B автомата SB .
1.3.6. Пример преобразования автомата Мили в автомат Мура 
Рассомотрим пример преобразования автомата Мили, изображенного на рис. 1-2, в автомат Мура. В автомате Мили Za={Z1, Z2}, Wa={W1, W2}, Aa= {A1,A2,A3}, а1A= а1,  A и
A и  A определяются графом автомата. В эквивалентном автомате Мура
A определяются графом автомата. В эквивалентном автомате Мура
ZB = ZA = {Z1, Z2}, WB = WA = {W1, W2}.
1. Построим множество AB, для чего найдем множество пар, порождаемых каждым состоянием автомата SA:
A1={(a1, W1), (a1, W2)} ={b1,b 2};
A2={(a2, W1)}={b3};
A3={(a3, W1) (a3, W2)}={b4 ,b5};
AB=A1U A2U A3={b1,b2,b 3,b4,b5}.
2. C каждым состоянием, представляющем собой пару, отождествим выходной сигнал, являющийся вторым элементом этой пары:
 B(b1) =
B(b1) =  B (b3) =
B (b3) =  B(b4) = W1
B(b4) = W1
 B(b2) =
B(b2) =  B(b5) = W2
B(b5) = W2
3. Рассматривая каждую пару и каждую связь, получим: так как в автомате SA из состояния а1 есть переход под действием сигнала z1 в состояние а3 с выдачей сигнала W1, то из множества A1 = {b1, b2} порождаемых состоянием а1 в автомате Мура SB должен быть переход в состояние {a3, W1}=b4 под действием сигнала z1.
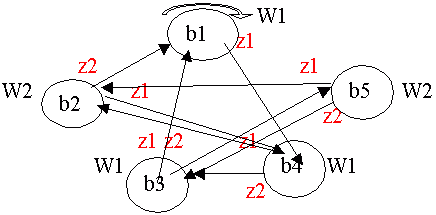
Аналогично с состоянием A1 должен быть переход в состояние {a1, W1} = b1 под действием сигнала z2 и так далее. В качестве начального состояния можно выбрать любую b1,b2 А1. Если сагналы bi заменить на аi, то получим стандартное представление автомата Мура.
1.3.7. Пример перехода от автомата Мили с переходящим состоянием к автомату Мура 
Рассмотрим переход от автомата Мили к автомату Мура, у которого входное состояние является переходящим. Будем составлять множество состояний следующим образом:
A1U A2U A3={(a2, W1) (a2, W2) (a3, W1) (a3, W2)} = {b2,b3,b4, b5}.
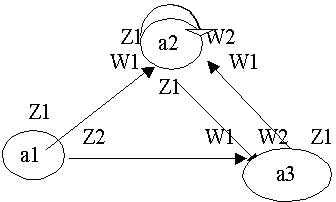
К этим состояниям добавим пару (а1, -) = b1. Где " - " означает, что выходной сигнал в состоянии b1 не определен. Функцию переходов SB будем определять как и раньше.
Из данного графа получим граф:

В качестве начального состояния автомата Мура можно взять порождаемое им состояние.
Эквивалентность автоматов SB и SA при преобразовании автомата Мили в автомат Мура на множестве входных слов конечной длины легко доказать по индукции подобно изложенному выше при обратном преобразовании.
Методы взаимной транспозиции автоматов Мили и Мура показывают, что при переходе от автомата Мили к автомату Мура число состояний принципиально не меняется. В то время как при обратном переходе в автомат Мура число состояний, как правило, увеличивается. Вследствие транзитивности отношения эквивалентности два автомата Мили, первый из которых получен из автомата Мура, так же будут эквивалентны, но у второго автомата число состояний будет больше. Таким образом эквивалентные между собой автоматы могут иметь различное число состояний. В связи с чем и возникает задача нахождения минимального автомата в классе эквивалентных между собой автоматов. Существование для любого абстрактного автомата эквивалентного ему абстрактного автомата с минимальным числом внутренних состояний впервые было доказано Муром.
1.4. Минимизация полностью определенных автоматов 
1.4.1. Теоретические основы минимизации 
Рассмотрим алгоритм минимизации полностью определенных абстрактных автоматов Мили, предложенный Ауфенкампом и Хоном. Основная идея этого метода состоит в разбиении всех состояний исходного абстрактного автомата на попарно не пересекающиеся классы эквивалентных состояний и замене каждого класса эквивалентности одним состоянием. Таким образом, получающийся в результате минимальный автомат имеет столько же состояний, на сколько классов эквивалентности разбиваются состояния исходного автомата.
Два состояния автомата аm и аs называются эквивалентными аm ~ аs, если  (аm,
(аm, 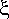 ) =
) =  (аs,
(аs, 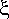 ) для всевозможных входных слов
) для всевозможных входных слов 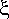 . Если аm и аs не эквивалентны, они различимы. Более слабой эквивалентностью является k - эквивалентность.
. Если аm и аs не эквивалентны, они различимы. Более слабой эквивалентностью является k - эквивалентность.
Состояния аm и аs k -эквивалентны аm ~ аs , если  (аm,
(аm, 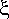 k) =
k) =  (аs,
(аs, 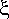 k) для всевозможных входных слов
k) для всевозможных входных слов 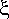 k длины k.
k длины k.
Если состояния не k -эквивалентны, они k -различимы. Введенные отношения эквивалентности и k - эквивалентности рефлексивны, симетричны, транзитивны. Следовательно, они являются отношениями эквивалентности и могут быть использованы для разбиения множества А состояний автомата на попарно не пересекающиеся классы. Соответствующие разбиения на класы эквивалентных и k -эквивалентных состояний будем обозначать  и
и  k. Разбиение
k. Разбиение  позволяет определить избыточные элементы в множестве состояний А. Пусть, например, аm и аs эквивалентны. Это значит, что сточки зрения реакций автомата на всевозможные входные слова неважно, находится автомат в состоянии аm или аs, и одно и них, например аs , может быть удалено из множества А. Если каждый класс эквивалентности содержит только одно состояние, множество А несократимо. Если же один или несколько класов содержат более одного элемента, все элементы, кроме одного в каждом класе, могут быть исключены из множества А, в результате чего получается автомат с минимальным числом состояний.
позволяет определить избыточные элементы в множестве состояний А. Пусть, например, аm и аs эквивалентны. Это значит, что сточки зрения реакций автомата на всевозможные входные слова неважно, находится автомат в состоянии аm или аs, и одно и них, например аs , может быть удалено из множества А. Если каждый класс эквивалентности содержит только одно состояние, множество А несократимо. Если же один или несколько класов содержат более одного элемента, все элементы, кроме одного в каждом класе, могут быть исключены из множества А, в результате чего получается автомат с минимальным числом состояний.
1.4.2. Алгоритм минимизации 
Пусть автомат S = {A, Z, W,  ,
,  , а1} подвергается минимизации. Этот процесс состоит из:
, а1} подвергается минимизации. Этот процесс состоит из:
1. Находятся последовательные разбиения  1,
1,  2,:,
2,:,  k,
k,  k+1 множества А на классы одно-, двух-,:, k-, k+1 эквивалентных состояний, до тех пор пока на каком-то k+1 шаге не окажется, что
k+1 множества А на классы одно-, двух-,:, k-, k+1 эквивалентных состояний, до тех пор пока на каком-то k+1 шаге не окажется, что  k+1=
k+1=  k. Нетрудно показать, что тогда разбиение
k. Нетрудно показать, что тогда разбиение  k =
k =  , то есть что k- эквивалентные состояния являются в этом случае эквивалентными и число шагов k, при котором
, то есть что k- эквивалентные состояния являются в этом случае эквивалентными и число шагов k, при котором  k =
k =  не превышает М-1, где М - число элементов в множестве А.
не превышает М-1, где М - число элементов в множестве А.
2. В каждом классе эквивалентности разбиения  выбираются по одному элементу, которые образуют множество А' состояний минимального автомата S' = {A', Z, W,
выбираются по одному элементу, которые образуют множество А' состояний минимального автомата S' = {A', Z, W,  ,
,  , а'1}, эквивалентного автомату S.
, а'1}, эквивалентного автомату S.
3. Функции переходов  ' и
' и  ' автомата S' определяются на множестве A' x Z. Для этого в таблице переходов и выходов вычеркиваются столбцы, соответсвующие не вошедшим в множество А' состояниям, а в оставшихся столбцах таблицы переходов все состояния заменяются на эквивалентные из множества A'.
' автомата S' определяются на множестве A' x Z. Для этого в таблице переходов и выходов вычеркиваются столбцы, соответсвующие не вошедшим в множество А' состояниям, а в оставшихся столбцах таблицы переходов все состояния заменяются на эквивалентные из множества A'.
4. В качестве а'1 выбирается одно из состояний, эквивалентное состоянию а1. В частности, удобно за а'1 принимать само а1.
1.4.3. Пример минимизации автомата Мили 
T1-10.Таблица переходов не минимального автомата Мили

T1-11. Таблица выходов не минимального автомата Мили

Непосредственно по таблице выходов  получаем разбиение
получаем разбиение  1 на классы одноэквивалентных состояний, объединяя в эквивалентные классы одинаковые столбцы:
1 на классы одноэквивалентных состояний, объединяя в эквивалентные классы одинаковые столбцы:  1={b1,b2} b1={a1,a 2,a5,a7,a8} b2={a3,a4,a6, a9,a10,a11,a12}. Действительно, два состояния 1 - эквивалентны, если их реакции на всевозможные входные слова длины 1 совпадают, то есть соответствующие этим состояниям столбцы в таблице выходов должны быть одинаковы.
1={b1,b2} b1={a1,a 2,a5,a7,a8} b2={a3,a4,a6, a9,a10,a11,a12}. Действительно, два состояния 1 - эквивалентны, если их реакции на всевозможные входные слова длины 1 совпадают, то есть соответствующие этим состояниям столбцы в таблице выходов должны быть одинаковы.
Строим таблицу  1, заменяя состояния в таблице переходов соответствующими классами 1 -эквивалентности.
1, заменяя состояния в таблице переходов соответствующими классами 1 -эквивалентности.
T1-12.Разбиение  1 состояний автомата Мили.
1 состояний автомата Мили.

Очевидно, что 1 -эквивалентные состояния аm и аs будут 2 - эквивалентными, если они переводятся любым входным сигналом также в 1 - эквивалентные. По таблице 1-12 получаем разбиение  2={C1,C2,C3,C 4}; C1= {a1,a2}, C2={a5,a7,a8 }, C3={a3,a4,a6,a9,a11}, C4= {a10,a12}.
2={C1,C2,C3,C 4}; C1= {a1,a2}, C2={a5,a7,a8 }, C3={a3,a4,a6,a9,a11}, C4= {a10,a12}.
T1-13.Разбиение  2 состояний автомата Мили.
2 состояний автомата Мили.

Аналогично построим  3 ={D1,D2,D3,D4, D5}; D1={a1,a2}, D2={a5,a7}, D3={a8}, D4={a3,a4,a6,a9,a11 }, D5={a10,a12} и, наконец
3 ={D1,D2,D3,D4, D5}; D1={a1,a2}, D2={a5,a7}, D3={a8}, D4={a3,a4,a6,a9,a11 }, D5={a10,a12} и, наконец  4 ={E1 ,E2,E3,E4,E5}, которое совпадает с
4 ={E1 ,E2,E3,E4,E5}, которое совпадает с  3. Процедура разбиения завершена. Разбиение
3. Процедура разбиения завершена. Разбиение  3 есть разбиение множества состояний автомата Мили на классы эквивалентных между собой состояний.
3 есть разбиение множества состояний автомата Мили на классы эквивалентных между собой состояний.
T1-14.Разбиение  3 состояний автомата Мили.
3 состояний автомата Мили.

Вычеркиваем из D1 а2, из D2 а7, из D4 а4, а6, а9, а11, из D5 а12 определяем минимальный автомат Мили.
T1-15.Таблица переходов минимального автомата Мили.
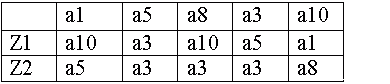
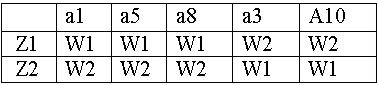
T1-16.Таблица выходов минимального автомата Мили.
1.4.4. Пример минимизации автомата Мура 
При минимизации автоматов Мура вводится понятие 0 -эквивалентности состояний и разбиение множества состояний на 0 -классы: 0 -эквивалентными называются любые одинаково отмеченные состояния автоматов Мура. Если два 0 -эквивалентных состояния любым входным сигналом переводится в два 0 -эквивалентных состояния, то они назаваются 1 -эквивалентными. Все дальнейшие классы эквивалентности состояний для автоматов Мура определяются аналогично приведенному выше для автоматов Мили.
T1-17. Отмеченная таблица переходов неминимального автомата Мура.

В результате применения алгоритма минимизации к автомату Мура, имеющему 12 состояний, получим автомат Мура, имеющий 4 состояния. Отпуская промежуточные таблицы, приведем лишь последовательность разбиений:  0 = {B1, B2, B3}.
0 = {B1, B2, B3}.
T1-18. Отмеченная таблица переходов минимального автомата Мура.

B1={a1, a2, a8}; B2={a6, a9, a10, a11, a12}; B3={a3, a4, a5, a7}
 1 ={C1, C2, C3, C4}.
1 ={C1, C2, C3, C4}.
C1={ a1, a2, a8}; C2={ a6, a9, a11}; C3={ a10, a12}; C4={ a3, a4, a5, a7}
 2 ={D1, D2, D3, D4};
2 ={D1, D2, D3, D4};
 2 =
2 =  1;
1;
D1 = C1; D2 = C2; D3 = C3; D4 = C4.
1.5. Совмещенная модель автомата (С- автомат) 
Под абстрактным С -автоматом будем понимать математическую модель дискретного устройства, определяемую множеством из 8 элементов
S={A, Z, W, U, a1,  ,
,  1,
1,  2},где
2},где
A={a1,:,am,:,aM} - множество состояний;
Z={z1,:, zf,:,zF} - множество входных сигналов;
W={w1,:,wg,:,wG} - множество выходных сигналов типа 1;
U={u1,:,uh,:,uH} - множество выходных сигналов типа 2;
a1 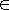 A - начальное состояние;
A - начальное состояние;
 - функция переходов, реализующая отображение множества D
- функция переходов, реализующая отображение множества D 
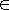 A x Z в A;
A x Z в A;
 1 - функция выходов, реализующая отображение множества D
1 - функция выходов, реализующая отображение множества D  1
1 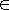 A x Z на W;
A x Z на W;
 2 - функция выходов, реализующая отображение множества D
2 - функция выходов, реализующая отображение множества D  2
2 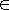 A на U.
A на U.

Рис. 1-14. Абстрактный автомат.
Абстрактный С -автомат можно представить в виде устройства с одним входом, на который поступают сигналы из входного алфавита Z, и двумя выходами, на которых появляются сигналы из алфавитов W и U. Отличие С -автомата от моделей Мили и Мура состоит в том, что он одновременно реализует две функции выходов  1 и
1 и  2, каждая из которых характерна для этих моделей в отдельности. С -автомат можно описать следующими уравнениями:
2, каждая из которых характерна для этих моделей в отдельности. С -автомат можно описать следующими уравнениями:
a(t+1)=  (a(t), z(t)); w(t)=
(a(t), z(t)); w(t)=  1(a(t), z(t)); u(t)=
1(a(t), z(t)); u(t)=  2(a(t)), t=0,1,2,:
2(a(t)), t=0,1,2,:
Выходной сигнал uh =  2(аm) выдается все время, пока автомат находится в некотором состоянии аm. Выходной сигнал wg =
2(аm) выдается все время, пока автомат находится в некотором состоянии аm. Выходной сигнал wg =  1(am, zf) выдается во время действия входного сигнала zf при нахождении автомата в состоянии аm. Очевидно что от С -автомата легко перейти к автоматам Мили или Мура, так же как возможна трансформация автомата Мили в автомат Мура и наоборот. Для создания С -автоматов будем также использовать табличный и графический методы. В первом случае таблица переходов (табл. 1-19) аналогична таблице переходов автомата Мили, а в таблице выходов каждое состояние отмечено соответствующим ему сигналом типа 2 (табл. 1-20). При задании С -автомата в виде графа сигналы типа 1 будем приписывать дугам графа рядом с входными сигналами, а сигналы типа 2- вершинам- состояниям, которым они соответствуют.
1(am, zf) выдается во время действия входного сигнала zf при нахождении автомата в состоянии аm. Очевидно что от С -автомата легко перейти к автоматам Мили или Мура, так же как возможна трансформация автомата Мили в автомат Мура и наоборот. Для создания С -автоматов будем также использовать табличный и графический методы. В первом случае таблица переходов (табл. 1-19) аналогична таблице переходов автомата Мили, а в таблице выходов каждое состояние отмечено соответствующим ему сигналом типа 2 (табл. 1-20). При задании С -автомата в виде графа сигналы типа 1 будем приписывать дугам графа рядом с входными сигналами, а сигналы типа 2- вершинам- состояниям, которым они соответствуют.

Нетрудно показать, что к полностью определенному С -автомату можно применить алгоритм минимизации Ауфенкампа- Хона, если под одноэквивалентными понимать состояния, которые одинаково отмечены и имеют одинаковые столбцы в таблице выходов. Проводя последовательность разбиений на 1-, 2-,:, k-, k+ 1 - эквивалентные классы до совпадения разбиений  k+ 1 и
k+ 1 и  k получим разбиение множества состояний на эквивалентные, после чего замена каждого класса эквивалентности одном состоянием дает минимальный С -автомат. В результате применения такого алгоритма к автомату, заданному таблицами 1-21 и 1-22, получим минимальный С -автомат, представленный в таблице 1-23 и 1-24. Опуская промежуточные таблицы, приведем лишь последовательность разбиений при минимизации:
k получим разбиение множества состояний на эквивалентные, после чего замена каждого класса эквивалентности одном состоянием дает минимальный С -автомат. В результате применения такого алгоритма к автомату, заданному таблицами 1-21 и 1-22, получим минимальный С -автомат, представленный в таблице 1-23 и 1-24. Опуская промежуточные таблицы, приведем лишь последовательность разбиений при минимизации:
|
|
|
|
|
Дата добавления: 2015-05-09; Просмотров: 2920; Нарушение авторских прав?; Мы поможем в написании вашей работы!