Постоянный ток. Правила Кирхгофа

Задача 1

Дана цепь, изображенная на рис.. Определите силу тока в каждом элементе и напряжение на зажимах реостата, если E₁=12 В, r ₁=1 Ом, E₂=6 В, r ₂=1,5 Ом и R =20 Ом. Каковы параметры источника тока, эквивалентного двум данным, соединенным параллельно?

Указания. Применяя законы Кирхгофа, следует соблюдать следующие правила:

1.Перед составлением уравнений произвольно выбрать и на чертеже: а) направления токов (если они не заданы по условию задачи) во всех сопротивлениях, входящих в цепь; б) направление обхода контуров.

2. При составлении уравнений по первому закону Кирхгофа принято считать токи, подходящие к узлу, положительными, а токи, выходящие из узла – отрицательными.

Число уравнений, составляемых по первому закону Кирхгофа, должно быть на единицу меньше числа узлов, содержащихся в цепи.

3. При составлении уравнений по второму закону Кирхгофа принято считать: а) падение напряжения на участке цепи (т.е. произведение Ir) входит в уравнение со знаком плюс, если направление тока в данном участке совпадает с выбранным направлением обхода контура; в противном случае произведение Ir входит в уравнение со знаком минус; б) ЭДС входит в уравнение со знаком плюс, если она повышает потенциал в направлении обхода контура, т.е. если при обходе контура приходится идти от минуса к плюсу внутри источника тока; в противном случае ЭДС входит в уравнение со знаком минус.

Число независимых уравнений, которые могут быть составлены по второму закону Кирхгофа, должно быть меньше числа замкнутых контуров, имеющихся в цепи. Для составления уравнений первый контур можно выбирать произвольно. Все последующие контуры следует выбирать таким образом, чтобы в каждый новый контур входила хотя бы одна ветвь цепи, не участвовавшая ни в одном из ранее использованных контуров. Если при решении уравнений, составленных указанным выше способом, получены отрицательные значения силы тока или сопротивления, то это означает, что ток через данное сопротивление в действительности течет в направлении, противоположном произвольно выбранному.

Указания по решению.

На данной схеме есть m =2 узла: А и В. Сходящиеся в них токи одинаковы, поэтому первое правило Кирхгофа в данном случае дает лишь одно уравнение (m – 1=2 – 1=1, например, для узла В):

.

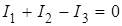Т.к. число ветвей в данной цепи р =3, то независимых контуров в схеме будет 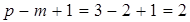: АСDB и ABNM, они являются элементарными контурами цепи. В направлении указания обозначений, т.е. по часовой стрелке, выберем и положительное направление обхода каждого из них. Записываем еще 2 уравнения на основе (6.2) для указанных контуров соответственно:

Получаем систему из трех уравнений для искомых сил токов в ветвях, которая, после подстановки числовых данных из условия задачи, принимает вид: Находим решение этой системы: I ₁=2,68 А, I ₂=-2,214 А,

I ₃=0,466 А.

Отсюда ясно, что истинное направление тока через второй элемент противоположно указанному на рисунке. Падение напряжения на зажимах реостата 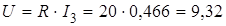(В).

Задача 2

. Определите напряженность электрического поля в алюминиевом проводнике объемом V =10 см³, если при прохождении по нему постоянного тока в течение t =5 мин выделилось Q =2,3 Дж теплоты.

Указания по решению.

Количество теплоты Q, выделившейся в алюминиевом проводнике сопротивлением R при прохождении по нему постоянного тока I в течение времени t, находится по закону Джоуля-Ленца в интегральной форме:

.

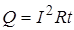Из условия задачи не ясно, какова форма проводника, поэтому будем считать его линейным и его сопротивление считаем равным

,

где - удельное сопротивление алюминия (табличная величина), l – его длина, S - площадь поперечного сечения, которую считаем постоянной.

Искомую напряженность электрического поля в проводнике выразим:

.

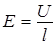Осталось записать связь между током, напряжением на концах проводника и его сопротивлением в соответствии с законом Ома для однородного участка «данный алюминиевый проводник»:

.

Мы рассмотрели 4 основные взаимосвязи между величинами, прямо или косвенно затронутыми в условии задачи. Попытаемся, исходя из этого, найти искомую величину. Для этого подставим в первое равенство последующие три:

,

отсюда и получается решение задачи в общем виде.

Завершите самостоятельно решение задачи, сделайте проверку размерностей и получите числовой результат.

Задача 3

Сила тока в проводнике сопротивлением R =10 Ом за время D t =50 с равномерно возрастает от I ₁=5 А до I ₂=10 А. Определите: 1) заряд, протекший через поперечное сечение проводника за указанное время; 2) количество теплоты, выделившееся за это время в проводнике.

Указания по решению.

При решении этой задачи будем использовать 2 метода: графический и так называемый «метод среднего», а также аналогию с кинематикой материальной точки.

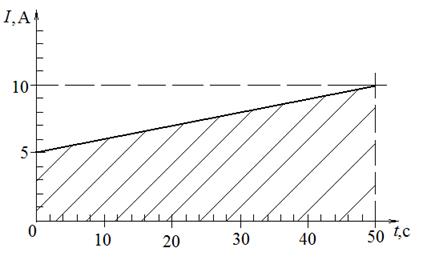
Построим график изменения со временем силы тока в проводнике (рис. 24).

рис. 24

1) Будем искать заряд, прошедший через поперечное сечение проводника за заданное время. При этом, как видно из рис. 24, начало отсчета времени совпадает в моментом, когда сила тока в проводнике равна I ₁.

I способ (графический). Известно из кинематики, что при неравномерном прямолинейном движении тела (когда скорость меня­ется по величине) в тече­ние некоторого проме­жутка времени пройден­ный за это время путь графически представля­ется площадью криволи­нейной трапеции под гра­фиком зависимости v (t) в соответствующем рассматриваемому отрезку движения временном интервале. Аналогично (с учетом таблицы 2 на стр. 70) искомый заряд равен площади за­штрихованной фигуры на рис. 24, т.е. q =375 Кл.

II способ («метод среднего»). Из кинематики известно, что в случае равномерного возрастания скорости (равноускоренное движение) средняя на участке скорость равна среднему арифметическому от значений скорости в начале и в конце рассматриваемого участка движения. По аналогии найдем в данном случае среднее значение силы тока:

(А).

Тогда также, как, зная среднюю скорость, находится весь пройденный путь, суммарный прошедший через поперечное сечение заряд будет равен

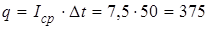(Кл).

Легко видеть, что полученные разными способами результаты совпадают.

2) Будем теперь искать количество теплоты, выделившееся за это время в проводнике.

Прежде всего, найдем искомое значение в соответствии с законом Джоуля-Ленца:

, (*)

где, согласно таблице 2, сила тока меняется по закону

.

Подставляем и вычисляем

=29,17 (кДж).

Задача 4

Определить плотность тока в медной проволоке длиной ℓ=10 м, если разность потенциалов на ее концах j₁-j₂=12 В.

Решение. Плотность тока, определяемую формулой j=di/dS, найдем, выразив силу тока по закону Ома для участка однородной цепи I=(j₁-j₂)/R. Тогда с учетом R=rℓ/S получим I=(j₁-j₂)S/(rℓ).

Отсюда плотность тока j=di/dS=(j₁-j₂)/(rℓ). (1)

К такому же выводу можно прийти, применив закон Ома в дифференциальной форме j=gE, предварительно выразив напряженность электрического поля внутри проводника через разность потенциалов на концах проводника и его длину: E=(j₁-j₂)/ℓ.

С учетом r=1/g,будем иметь:

j=(j₁-j₂)/(rℓ).

Выбрав из справочных таблиц значение удельного сопротивления меди и выполнив вычисление, найдем j=7×10⁷ (А/м).

Дата добавления: 2015-05-07