
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Математичні основи роботи комп’ютера
|
|
|
|
Логічні величини та логічні операції. Розв'язуючи задачі з математики, фізики та хімії, ми оперуємо даними. Цими даними є числа. Ми вміємо виконувати дії з числовими даними: додавання, віднімання, множення, ділення, піднесення до степеня і знаємо, що такі дії мають різний пріоритет.
Але виявляється, що окрім числових даних, в інформатиці існують інші типи даних, наприклад, логічні.
Логічні дані та дії, визначені над ними, утворюють булеву алгебру, названу на честь її творця — англійського математика Джорджа Буля (1815-1864). Уже значно пізніше виявилося, що функціонування багатьох електронних пристроїв (лічильників, суматорів, шифраторів, дешифраторів тощо) описується формулами булевої алгебри. Одним із різновидів булевої алгебри є — алгебра висловів.
Алгебру висловів утворюють вислови та логічні операції над ними.
Вислів —це розповідне речення, яке може бути або істинним, або хибним.
Якщо вислів відповідає дійсності, то він істинний, у протилежної випадку — хибний. Наприклад, нехай відомо, що Х=10. Тоді вислів «Х>5» є істинним, а вислів «Х<5» є хибним.
Вислови є логічними величинами. Як і числові, логічні величні можуть бути сталими або змінними. Якщо вислів, позначений іменем А, є істинним, то пишуть А=1, якщо хибним, то пишуть А=0. Тут 1 і 0 — логічні сталі. Є лише дві логічні сталі: 1 і 0. Логічні змінні позначають літерами. Змінні можуть набувати значення 1 або 0, тобто «істина» або «хибність».
Є три основні логічні операції над логічними величинам:
1) «НЕ» (інші назви: інверсія, логічне заперечення; символ операції « » пишеться над величиною);
» пишеться над величиною);
2) «І» (кон'юнкція, логічне множення; символ «•» або «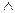 »);
»);
3) «АБО» (диз'юнкція, логічне додавання; символ «+» або «v»).
Послідовність виконання операцій така: спочатку виконуються операції «НЕ», пізніше — операції «І», останніми— операції «АБО».
Позначимо аргументи літерами А і В, арезультат логічної операції — літерою С.
Означення 1. Операція «НЕ», застосована до А, дає протилежне значення А.
Означення 2. Операція «І», застосована до А і В, дає значення 1 тільки тоді, коли А = 1 і В = 1, і значення 0 у всіх інших випадках.
Означення 3. Операція «АБО», застосована до А та В, дає значення 1, якщо хоча б одна змінна А або В має значення 1, і значення 0, якщо А = 0 і В = 0.
Дані означення можна проілюструвати засобами таблиць істинності.
| Операція«НЕ» | Onерація «І» | Операція «АБО» | |||||||
| А | С= 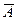
| А | В | С=А∙В | А | В | С=А+В | ||
| 1 0 | 0 1 | 1 1 0 0 | 1 0 1 0 | 1 0 0 0 | 1 1 0 0 | 1 0 1 0 | 1 1 1 0 |
Основні формули алгебри логіки. Вислови, для яких результатуючі стовпці в таблиці істинності збігаються, називаються рівносильними. Для позначення рівносильних висловів використовують символ «=», який слід читати так: рівносильно.
Для операцій «І» та «АБО» виконуються переставний та сполучний закони:
А + В = В + А, (А + В) + С = А + (В + С); А∙В = В∙А, (А∙В) ∙С =А∙ (В∙С).
Основні формули алгебри логіки (властивості логічних операцій).
Операція «НЕ»
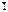 =0 =0
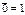
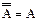
| Операція «1»
А∙ 1=А
А ∙ 0=0
А ∙ А=А
А ∙ 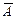 =0 =0
| Операція «АБО» А+1=1
А+0=А
А+А=А
А+ 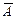 =1 =1
|
За допомогою формул алгебри логіки описують функціонування фізичних пристроїв, а також розв'язують різноманітні логічні задачі.
Як і алгебричні вирази, громіздкі логічні формули потрібно спрощувати, щоб у них було якнайменше операндів.
Елементи теорії автоматів. Логічні формули застосовують для побудови (синтезу) автоматів. Розглянемо найпростіші (без елементів пам'яті) автомати — пристрої, які перетворюють вхідні потоки інформації, що складається з одного чи багатьох сигналів, у вихідні.
Сигнали бувають двох типів. Їх умовно позначають «1» і «0». Автомат можна сконструювати, маючи логічну формулу, за допомогою елементарних пристроїв, які реалізують логічні операції «НЕ», «І», «АБО».
Етапи створення автомата:
Задача => логічна формула => логічна схема => фізична схема => виготовлення пристрою.
Схеми трьох логічних операцій.

Схеми для oперацій «І» та «АБО» мають два або більше входів.
Логічній формулі відповідає комбінація схематичних позначень. Це і є логічна схема автомата.
Маючи логічну схему, потрібно побудувати фізичну схему, наприклад, електричну. Для цього в логічній схемі замінюють позначення логічних операцій електричними схемами. Таким чином отримують повну електричну схему автомата, яка є кінцевим результатом роботи конструктора.
|
|
|
|
|
Дата добавления: 2015-05-07; Просмотров: 682; Нарушение авторских прав?; Мы поможем в написании вашей работы!