Истечение и дросселирование газов и паров

З-8.6

З-8.5

З-8.4

З-8.3

З-8.2

З-8.1

Задачи

Решение.

П-8.2

Найти массу, внутреннюю энергию, энтальпию и энтропию 6 м³ насыщенного водяного пара при давлении р =1,2 МПа и степени сухости пара х =0,9.

Значения внутренней энергии, энтальпии и энтропии определяем по формулам из таблицы 5 для насыщенного водяного пара, принимая необходимые для них исходные данные по приложению А

Удельный объем влажного пара

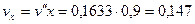м³/кг.

Масса пара

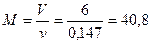кг.

Энтальпия пара

кДж.

Внутренняя энергия пара

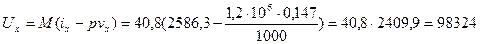кЖд.

Энтропия пара

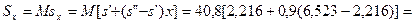
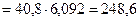кДж/К.

В барабане котельного агрегата находится кипящая вода и над ней водяной пар под давлением р =9 МПа. Масса воды М =5000 кг. Объем барабана V =8 м³.

Какова масса пара, находящегося над зеркалом испарения, если пар считать сухим насыщенным?

Ответ: М_П =45 кг.

В трубе течет водяной пар при давлении р =2 МПа и степени сухости х =0,96 со скоростью w =40 м/с. Расход пара m =5000 кг/ч.

Определить внутренний диаметр трубы.

Ответ: d =65 мм.

К питательной воде, вводимой в прямоточный паровой котел при р =24 МПа и t =350 ºС в количестве D =900·10³ кг/ч, от топочных газов подводится Q = 1600 ГДж/ч теплоты.

Определить температуру пара на выходе из парового котла, его энтальпию и внутреннюю энергию. Падением давления при протекании воды и пара по трубам пренебречь.

Представить процесс в Т-s и i-s диаграммах.

Ответ: t₂ = 570 ºС, i₂ = 3403 кДж/кг, u₂ = 3069 кДж/кг.

Водяной пар массой 1 кг сжимается изотермически. При этом состояние пара меняется так, что начальные его параметры р₁ = 3,0 МПа и t₁ = 360 ºС, а конечные соответствуют состоянию кипящей жидкости.

Определить параметры в конце процесса и количество отведенной теплоты.

Ответ: р₂ =18,67 МПа, v”₂ =0,001894 м³/кг, i”₂ =1762 кДж/кг, s”₂ =3,9162 кДж/(кг·К), q = -1809 кДж/кг.

Определить количество теплоты, затрачиваемой на перегрев 1 кг влажного пара при давлении р = 10 МПа и степени сухости х =0,98 до температуры t =480 ºС.

Ответ: q_П =621,6 кДж/кг.

В паровом котле объемом V =15 м³ находятся 4000 кг воды и пара при давлении 4 МПа и температуре насыщения.

Определить массы воды и сухого насыщенного пара, находящегося в котле.

Ответ: М_П =206 кг, М_В =3794 кг.

Истечение газов может происходить через каналы различной формы. Канал, в котором с уменьшением давления скорость газового потока возрастает, называется соплом, канал, в котором скорость газа уменьшается, а давление возрастает, называется диффузором.

При решении задач, связанных с истечением газа, наиболее распространенной является задача, связанная с истечением газа через сопло (насадку) из сосуда неограниченного объема. Процесс истечения газа из сопла теоретически происходит без теплообмена с окружающей средой, т.е. является адиабатным (q=0) и представлен на р - v и i-s диаграмме (рис. 8). Как правило, при решении подобных задач требуется определить скорость истечения и расход газа, проходящего через сопло.

Для этого необходимо знать отношение давлений р₂/р₁, которое сравнивают с критическим отношением давлений для данного вида газа, определяемым по формуле

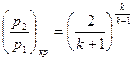, (9.1)

где р₁ - давление среды на входе в сопло;

р₂ – давление среды на выходе из сопла.

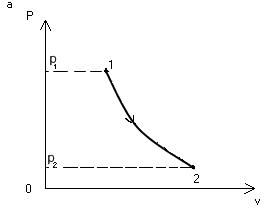
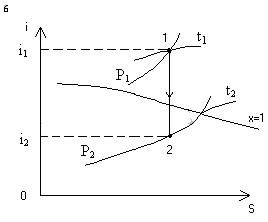
Рис. 8

В зависимости от формы канала и отношения давлений среды на выходе и на входе в канал скорость газового потока в выходном сечении канала может быть меньше, равной или больше скорости звука.

Критические отношения давлений для разных видов газов при адиабатном истечении показаны в таблице 6.

Таблица 6

Критические отношения давлений при истечении из сопла

Газы	Показатель адиабаты k	Отношение давлений (р2/р1)кр
Одноатомные	1,67	0,487
Двухатомные	1,4	0,528
Многоатомные	1,3	0,546

Таким образом, скорость истечения и расход газа могут определяться для двух случаев, когда (р₂/р₁)>(р₂/р₁)_кр и (р₂/р₁)≤(р₂/р₁)_кр:

а) (р₂/р₁)>(р₂/р₁)_кр.

Теоретическая (дозвуковая) скорость истечения газа из суживающегося сопла

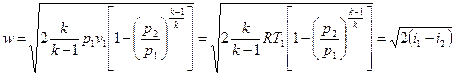, (9.2)

где v₁ – удельный объем газа на входе в сопло, м³/кг;

Т₁ – температура газа на входе в сопло, К.

i₁ и i₂ – соответственно энтальпии газа в начальном и конечном состоянии, Дж/кг.

Расход газа, вытекающего из сопла

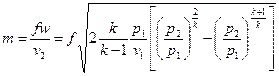, (9.3)

где f – площадь поперечного сечения выходного отверстия сопла, м².

б) При (р₂/р₁) ≤ (р₂/р₁)_кр, давление в среде, куда происходит истечение опускается до критического давления в устье сопла р_2кр и, соответственно, скорость и расход достигают своих критических (максимальных) значений.

Критическая скорость истечения газа из суживающегося сопла – это скорость распространения звука, которая устанавливается при данных параметрах среды у выходного сечения

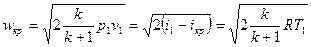, (9.4)

где i_кр – энтальпия при критическом давлении р_2кр, Дж/кг.

Скорость распространения звука в идеальном газе

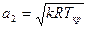, (9.5)

где Т – температура среды, равная Т_кр истечения газа, К.

Скорости w_кр и а₂ соответственно должны быть равны.

Максимальный расход газа, вытекающего из сопла

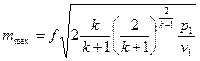, (9.6)

По формулам (9.2 – 9.6) можно определять скорость истечения и расход также для водяного пара, принимая при этом значения показателя адиабаты для перегретого пара k =1,3, для сухого насыщенного k =1,135, для влажного насыщенного k =1,035+0,1 х.

Для получения скоростей истечения выше критических применяется не сужающееся, а комбинированное – сужающе-расширяющееся сопло (сопло Лаваля) (рис. 9), параметры которого определяются по данным ниже формулам.

Площадь минимального сечения сопла

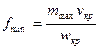, (9.7)

Площадь выходного сечения сопла

, (9.8)

Длина расширяющейся части сопла

, (9.9)

где d₂ и d_min – соответственно диаметры выходного и минимального сечения сопла, м;

α – угол конусности расширяющейся части сопла.

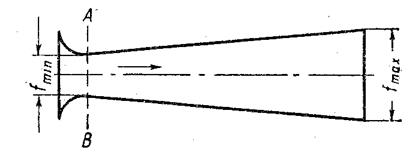
Рис. 9

Работа, совершаемая идеальным газом при адиабатном истечении

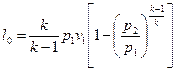, (9.10)

Сравнивая формулы (9.9) и (6.21) можно увидеть, что работа при истечении газа из сопла в k раз больше, чем работа просто адиабатного расширения газа.

Процесс прохождения газа через суженное сечение называется дросселированием. Дросселирование – это необратимый процесс, при котором давление р₂ за местом сужения всегда меньше, чем давление передним р₁. При этом никакой работы газ не совершает l₀ =0 и теплообмена с окружающей средой также не происходит, т.е. процесс является адиабатным. Удельный объем при дросселировании всегда возрастает v₂>v₁, температура идеальных газов не меняется, а температура реальных газов меняется, за исключением случая, когда она равна определенной начальной температуре – температуре инверсии

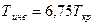, (9.11)

где Т_кр – критическая температура газа, К.

Энтальпия газа или пара при дросселировании в начальном и конечном состоянии одинакова

i₁=i₂, (9.12)

Процесс дросселирования изображается на i-s диаграмме горизонтальной прямой по линии i =const (рис. 10).

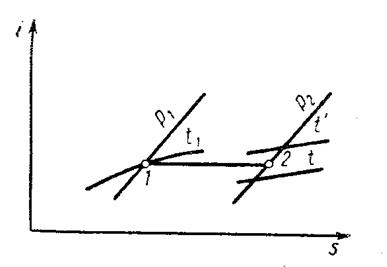
Рис. 10

Дата добавления: 2015-05-09