Второй закон термодинамики

З-6.12

З-6.11

З-6.10

З-6.9

З-6.8

З-6.7

З-6.6

З-6.5

З-6.4

З-6.3

З-6.2

З-6.1

Задачи

Определить среднюю массовую теплоемкость при постоянном объеме для азота в пределах 200-800 ºС, считая зависимость теплоемкости от температуры нелинейной. Средняя мольная теплоемкость азота при постоянном давлении может быть определена по формуле

.

Ответ. с_vm = 0,8122 кДж/(кг·К).

К 1 м³ воздуха, находящемуся в цилиндре со свободно движущимся нагруженным поршнем, подводится при постоянном давлении 335 кДж теплоты. Объем воздуха при этом увеличивается до 1,5 м³.

Начальная температура воздуха равна 15 ºС.

Какая устанавливается в цилиндре температура, и какова работа расширения? Зависимость теплоемкости от температуры считать линейной.

Ответ. t₂ = 159 ºС, L = 95,1 кДж.

Воздух в количестве 0,1 м³/с при t = 30 ºС и р = 0,1 МПа поступает в компрессор, где сжимается, а затем протекает между трубами холодильника, в которых движется охлаждающая вода.

Определить расход воды, если на выходе из компрессора воздух имеет параметры: t₁ = 200 ºС и р₁ = 0,8 МПа. Температура воздуха за холодильником t₂ = 40 ºС. Вода нагревается на t = 20 ºС.

Потерями теплоты и сопротивлением трения пренебречь.

Ответ: m =791 кг/ч.

При адиабатном расширении 1 кг воздуха (k =1,4 = const) температура его падает на 120 К.

Какова полученная в процессе расширения работа и сколько теплоты следовало бы подвести к воздуху, чтобы ту же работу получить в изотермическом процессе?

Ответ: l_ад = q_изот =86,1 кДж/кг.

В политропном процессе расширения окиси углерода энергия, выделяемая газом в форме работы, составляется за счет подводимой теплоты (25 %) и за счет уменьшения внутренней энергии газа (75 %).

Определить показатель политропы и теплоемкость процесса. Представить ход процесса в p-v диаграмме.

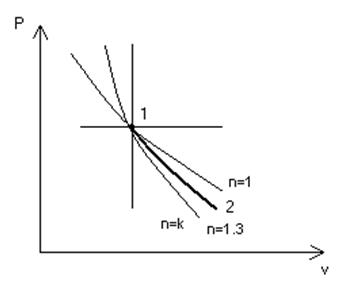
Рис. 4

Ответ: n =1,30; c_n = -0,247 кДж/(кг·К) (рис. 4).

В закрытом сосуде емкостью V = 0,3 м³ содержится 2,75 кг воздуха при давлении р₁ = 0,8 МПа и температуре t₁ = 25 ºС.

Определить давление и удельный объем после охлаждения воздуха до 0 ºС.

Ответ: р ₂ =0,732 МПа, v₂ =0,109 м³/кг.

Определить количество теплоты, необходимое для нагревания 2000 м³ воздуха при постоянном давлении р = 0,5 МПа от t₁= 1500 ºС до t₂= 600 ºС. Зависимость теплоемкости от температуры считать нелинейной.

Ответ: Q_p =3937 МДж.

8м³ воздуха при р₁ =0,09 МПа и t₁= 20 ºС сжимаются при постоянной температуре до 0,81 МПа.

Определить конечный объем, затраченную работу и количество теплоты, которое необходимо отвести от газа.

Ответ: V₂ =0,889 м³, Q = -1581 кДж.

Сосуд объемом 60 л заполнен кислородом при давлении
р₁ =12,5 МПа.

Определить конечное давление кислорода и количество сообщенной ему теплоты, если начальная температура кислорода t₁= 10 ºС, а конечная t₂= 30 ºС. Теплоемкость кислорода считать постоянной.

Ответ: р₂ =13,4 МПа, Q =133 кДж.

0,2м³ воздуха с начальной температурой 18 ºС подогревают в цилиндре диаметром 0,5 м при постоянном давлении р =0,2 МПа до температуры 200 ºС.

Определить работу расширения, перемещение поршня и количество затраченной теплоты, считая зависимость теплоемкости до температуры линейной.

Ответ: L =25000 Дж; h =0,64 м, Q =88,3 кДж.

Воздух при давлении р₁ =0,1 МПа и температуре t₁= 27 ºС сжимается в компрессоре до р₂ =3,5 МПа.

Определить величину работы L, затраченной на сжатие 100 кг воздуха, если воздух сжимается изотермически.

Ответ: L = -30576 кДж.

Воздух при давлении р₁ =0,45 МПа расширяясь адиабатно до 0,12 МПа, охлаждается до t₂ = -45 ºС.

Определить начальную температуру и работу, совершенную 1 кг воздуха.

Ответ: t₁= 61 ºС, l =75,3 кДж/кг.

Второй закон термодинамики определяет направление, в котором протекают процессы, устанавливает условия преобразования тепловой энергии в механическую, а также определяет максимальное значение работы, которая может быть произведена тепловым двигателем. Второй закон термодинамики математически может быть выражен формулой

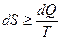, (7.1)

где dS – бесконечно малое приращение энтропии системы;

dQ – бесконечно малое количество теплоты, полученное системой от источника теплоты;

T –абсолютная температура источника теплоты.

Знак неравенства соответствует необратимым процессам, а знак равенства – обратимым. Следовательно, аналитическое выражение второго закона термодинамики для бесконечно малого обратимого процесса имеет вид

dq = TdS. (7.2)

Преобразуя уравнение (7.2) согласно первому закону термодинамики, используя выражения (5.2) и (5.4), получим

TdS = dU + pdV. (7.3)

Основным уравнением для определения изменения энтропии в обратимом процессе является выражение

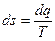. (7.4)

В теплотехнических расчетах приходится иметь дело с изменением энтропии Δs, а не с ее абсолютным значением, поэтому отсчет значений энтропии можно вести от любого ее состояния. Для газов принято считать значение энтропии равным нулю при н.у. Определение энтропии для любого состояния газа, отсчитанной от нормального состояния и определение изменения энтропии между двумя произвольными состояниями газа, производят по следующим формулам, приведенным в таблице 4.

Если работа совершается с помощью газа, параметры которого отличаются от параметров окружающей среды, то максимальная работа, которую может произвести этот газ, достижима лишь при условии его перехода от начального состояния к состоянию среды обратимым путем. При этом максимальная полезная работа меньше максимальной работы на величину работы вытеснения газа окружающей среды. Величина максимальной полезной работы определяется формулой

l_{max(полезн)} = u₁ – u₂ – T₀(s₁ – s₂) – p₀(v₂ – v₁). (7.5)

Таблица 4

Формулы для определения энтропии

Параметр	Энтропия, отсчитанная от нормального состояния, s	Изменение энтропии, Δs = s2 – s1
Переменная теплоемкость
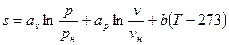
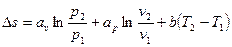
Постоянная теплоемкость

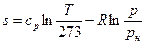
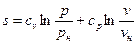
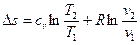
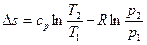
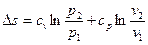
Так как выражения u₁ – u₂ и T₀(s₁ – s₂) представляют собой соответственно абсолютную величину работы адиабатного и изотермического процессов – уравнения (6.13) и (6.8), то формулу (6.34) можно представить в виде

l_{max(полезн)} = l_ад - l_из – p₀(v₂ – v₁). (7.6)

Дата добавления: 2015-05-09