Вопрос. Конвекция свободная и вынужденная. Основной закон конвективного теплообмена Ньютона-Рихмана. Теория подобия. Коэффициент теплоотдачи

Числовое значение коэф.теплопроводности определяет кол-во теплоты проходящее через единицу изотермии поверхности в единицу времени при условии что температурный коэф. Равен 1. Большое влияние на коэф. Теплопроводности оказывает влажность вещества.

Виды теплопроводности

Бывает:
-стационарная теплопроводность
-не стационарная теплопроводность

Коэффициент теплопроводности численно равен тепловому потоку проходящему в единицу времени изометрической поверхности при едином градиенте температуры.
Коэффициента теплопроводности зависит от давления и температуры.

Закон Фурье.

В установившемся режиме плотность потока энергии, передающейся посредством теплопроводности, пропорциональна градиентутемпературы:

где 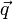— вектор плотности теплового потока — количество энергии, проходящей в единицу времени через единицу площади, перпендикулярной каждой оси, 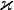— коэффициент теплопроводности (иногда называемый просто теплопроводностью), — температура. Минус в правой части показывает, что тепловой поток направлен противоположно вектору grad T (то есть в сторону скорейшего убывания температуры). Это выражение известно как закон теплопроводности Фурье. ^[1]

В интегральной форме это же выражение запишется так (если речь идёт о стационарном потоке тепла от одной гранипараллелепипеда к другой):

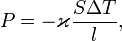
где — полная мощность тепловых потерь, 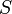— площадь сечения параллелепипеда, 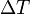— перепад температур граней, — длина параллелепипеда, то есть расстояние между гранями.

Теплопроводность через плоскую стенку.

Коэффициент теплопроводности является физическим параметром вещества, характеризующим его способность проводить теплоту. Коэффициент теплопроводности определяется из уравнения (9.4):

.

(9.8)

Численно коэффициент теплопроводности равен количеству теплоты, проходящему в единицу времени через единицу изотермической поверхности при условии gradt=1. Его размерность Вт/(м·К). Значения коэффициента теплопроводности для различных веществ определяются из справочных таблиц, построенных на основании экспериментальных данных. Для большинства материалов зависимость коэффициента теплопроводности от температуры приближенно можно выразить в виде линейной функции

.

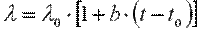(9.9)

где λ₀ — значение коэффициента теплопроводности при температуре t₀=0 ⁰С; b — постоянная, определяемая опытным путем.

Наихудшими проводниками теплоты являются газы. Коэффициент теплопроводности газов возрастает с увеличением температуры и составляет 0,006÷0,6 Вт/(м·К).

Теплопроводность через плоскую стенку при граничных условиях первого рода

Рис. 9.2. Однородная плоская стенка

Рассмотрим однородную плоскую стенку толщиной δ (рис. 9.2). На наружных поверхностях стенки поддерживаются постоянные температуры t_с1 и t_с2. Коэффициент теплопроводности стенки постоянен и равен λ. При стационарном режиме () и отсутствии внутренних источников теплоты (q_v =0) дифференциальное уравнение теплопроводности примет вид:

.

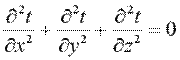(9.16)

При заданных условиях температура будет изменяться только в направлении, перпендикулярном плоскости стенки (ось Оx). В этом случае

,

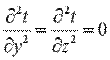
и дифференциальное уравнение теплопроводности перепишется в виде:

.

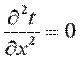(9.17)

Граничные условия первого рода запишутся следующим образом: при x=0 t=t_c1; при x=δ t=t_c2. Интегрируя уравнение (9.17), находим

.

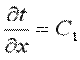После второго интегрирования получаем

.

(9.18)

Постоянные С₁ и С₂ определим из граничных условий: при x=0 t=t_c1, С₂=t_c1; при x=δ t=t_c2=С₁·δ+t_c1, отсюда 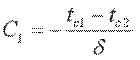. Подставляя значения С₁ и С₂ в уравнение (9.18), получим уравнение распределения температуры по толщине стенки:

.

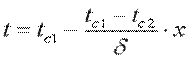(9.19)

Для определения плотности теплового потока, проходящего через стенку в направлении оси Оx, воспользуемся законом Фурье, согласно которому .

Учитывая, что 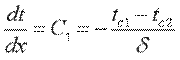, получим

.

(9.20)

Общее количество теплоты, которое передается через поверхность стенки F за время τ,

.

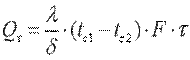(9.21)

Отношение 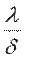называют тепловой проводимостью стенки, обратную ей величину 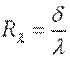- термическим сопротивлением теплопроводности. Поскольку величина λ зависит от температуры, в уравнения (9.20), (9.21) необходимо подставить коэффициент теплопроводности λ_с, взятый при средней температуре стенки.

Конвекция происходит только в газах и жидкостях. Это вид переноса теплоты осуществляется при перемещении и перемешивании всей массы неравномерно нагретой жидкостей и газа. Конвекционный перенос происходит тем интенсивнее чем больше скорости движения жидкости или газа, так как в этом случае за единицу времени перемещаются большее кол-во частиц тела.

Одновременный перенос теплоты конвекции и теплопроводностью называют конвективным теплообменом. Он может быть свободным и вынужденным. Если движение рабочего тела вызванного искусственно то такой конвективный теплообмен называется вынужденным. Если движение рабочего тела возникает под влиянием разности и плотности отдельных частей жидкостей от нагревания, то такой теплообмен называется свободным или естественным.

Дата добавления: 2015-05-09