Фазовые равновесия и фазовые переходы

В термодинамике фазой называется совокупность однородных, одинаковых по своим свойствам частей системы. Поясним понятие фазы на следующих примерах. В закрытом сосуде находится вода и над ней смесь воздуха и паров воды. В этом случае мы имеем дело с системой, состоящей из двух фаз: одну фазу образует вода, вторую – смесь воздуха и паров воды. Если в воду добавить несколько кусочков льда, то все эти кусочки образуют третью фазу. Различные кристаллические модификации какого-либо вещества также представляют собой разные фазы. Так, например, алмаз и графит является различными твердыми фазами углерода.

При определенных условиях разные фазы одного и того же вещества могут находиться в равновесии друг с другом, соприкасаясь между собой. Равновесие двух фаз может иметь место лишь в определенном интервале температур, причем каждому значению температуры Т соответствует вполне определенное давление Р, при котором возможно равновесие. Таким образом, состояние равновесия двух фаз изобразится на диаграмме (Р, Т) линией

.

Переход из одной фазы в другую обычно сопровождается поглощением или выделением некоторого количества теплоты, которое называется скрытой теплотой перехода, или просто теплотой перехода. Такие переходы называются фазовыми переходами первого рода. Существуют переходы из одной кристаллической модификации в другую, которые не связаны с поглощением или выделением теплоты. Такие переходы называются фазовыми переходами второго рода. Фазовые переходы второго рода не исчерпываются переходами между различными кристаллическими модификациями. К их числу принадлежит переход в сверхпроводящее состояние, совершаемый в отсутствие магнитного поля, а также переход между двумя жидкими фазами гелия, называемыми гелием I и гелием II. Мы ограничимся рассмотрением только переходов первого рода.

Классификацию фазовых переходов первого рода удобно провести с помощью следующей блок-схемы (рис.4.1):

1. плавление;

2. кристаллизация;

3. испарение;

4. конденсация;

5. конденсация;

6. сублимация.

Теплота фазового превращения D Q пропорциональна изменению массы фазы D m, т.е. 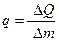- удельная теплота фазового превращения.

Фазовые превращения реального газа

Рассмотрим процесс сжатия вещества при постоянной температуре Т, которую выберем ниже критической Ткр. Первоначально вещество предполагают газообразным. Вначале по мере уменьшения объема давление газа будет расти (рис. 4.2).

По достижении объема V_Г давление перестает изменяться, а вещество перестает быть однородным – часть газа конденсируется в жидкость. Происходит расслоение вещества на две фазы: жидкую и газообразную. По мере дальнейшего уменьшения объема все большая часть вещества переходит в жидкую фазу, причем переход осуществляется при постоянном давлении Рн.п. (давлении насыщенного пара). После того как процесс конденсации вещества заканчивается (это происходит при достижении объема V_Ж), дальнейшее уменьшение объема начинает сопровождаться быстрым ростом давления.

На рис. 4.2 штриховой линией изображена изотерма Ван-дер-Ваальса, соответствующая данной температуре. Если проведем линию через крайние точки горизонтальных участков экспериментальных изотерм, получается колоколообразная, кривая, ограничивающая область двухфазных состояний вещества. Нарисуем на диаграмме (P, V) также изотерму, соответствующую критической температуре Ткр. Тогда колоколообразная кривая и критическая изотерма делят диаграмму (P, V) на четыре области (рис. 4.3).

Под колоколообразной кривой располагается область двухфазных состояний (жидкость+пар). Область, лежащая слева от колоколообразной кривой, представляет собой область однородных жидких состояний, и наконец, область, лежащая справа от колоколообразной кривой и верхней ветви критической изотермы, представляет собой область однородных газообразных состояний вещества. Здесь можно особо выделить часть, лежащую под правой ветвью критической изотермы, назвав ее областью пара. Любое состояние в этой области отличается от остальных газообразных состояний в том отношении, что при изометрическом сжатии вещество, первоначально находившееся в таком состоянии, претерпевает процесс сжижения. Вещество, находящееся в одном из состояний при температуре выше критической, не может быть сжижено никаким сжатием. Подразделение газообразных состояний на газ и пар не является общепринятым, поэтому в дальнейшем мы оба этих состояний будем называть газом.

Уравнение Клапейрона-Клаузиуса и фазовая диаграмма для превращения жидкость-газ (Ж«Г)

Как уже указывалось, две любые фазы вещества могут находиться в равновесии лишь при определенном давлении, величина которого зависит от температуры. Общий вид этой зависимости можно получить, воспользовавшись методом цикла Карно. Возьмем две близко расположенные изотермы реального газа при температурах Т и Т¢ =Т – dT. Построим на этих изотермах цикл Карно, как показано на рис.4.4. По теореме Карно имеем:

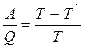(4.1)

В случае элементарного цикла Карно

.

Подставляя это в уравнение (4.1), получим:

(4.2)

Представим входящие в (4.2) величины следующим образом:

Q = ν r, V₁ = ν V_Ж, V₂ = ν V_Г,

где r – теплота испарения 1 моля жидкости; V_Ж – объем 1 моля жидкости,

V_Г – объем 1 моля газа.

Тогда уравнение (4.2) примет вид:

. (4.3)

Это уравнение Клапейрона-Клаузиуса для фазового превращения Ж«Г.

Фазовая диаграмма – это график, выражающий кривую Р = Р (Т), на которой две фазы находятся в равновесии. Уравнение Клапейрона-Клаузиуса (4.3) определяет характер этой кривой.

Поскольку (V_Г─V_Ж) > 0, то 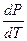> 0, т.е. повышение температуры приводит к увеличению равновесного давления.

Возьмем вещество в виде жидкости и находящегося в равновесии с ней насыщенного пара и, не изменяя объема, станем отнимать от него тепло. Этот процесс будет сопровождаться понижением температуры вещества и соответственно уменьшением давления. Поэтому точка, изображающая состояние вещества не диаграмме (Р, Т), перемещается вниз по кривой Р = Р (Т). Это продолжается до тех пор, пока не будет достигнута температура кристаллизации вещества, отвечающая равновесному значению давления (рис. 4.5).

Обозначим эту температуру Т_тр. Все время, пока идет процесс кристаллизации, температура и давление остаются неизменными. Отводимая при этом теплота представляет собой теплоту, выделяющуюся при кристаллизации. Температура Т_тр и соответствующее равновесное давление Р_тр – единственные значения температуры и давления, при которых могут находиться в равновесии три фазы вещества: твердая, жидкая и газообразная. Соответствующая точка на диаграмме Р (Т) называется тройной точкой А.

Уравнение Клапейрона-Клаузиуса и фазовая диаграмма для превращения твердое тело-жидкость (Т«Ж)

Уравнение Клапейрона-Клаузиуса в этом случае имеет вид аналогичный уравнению (4.3):

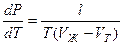(4.4)

где l – теплота плавления 1 моля твердого тела,

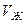- объем 1 моля жидкости, 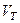- объем 1 моля твердого тела.

Р = Р (Т) – фазовая диаграмма, т.е. условие равновесия фаз. Обычно V _Ж> V _Т, и поэтому 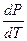>0, но для некоторых веществ (например, вода, чугун) V _Ж< V _Т, и тогда 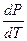<0. Вид фазовых диаграмм, для обоих случаев показан на рис.4.6 а и рис.4.6 б.

Уравнение

Уравнение Клапейрона-Клаузиуса и фазовая диаграмма для превращения твердое тело-газ (Т«Г). Тройная точка. Диаграмма состояния.

Возьмем вещество, которое находится в состоянии, когда три фазы вещества находятся в равновесии, т.е. в состоянии, заданным тройной точкой А. Будем продолжать отнимать от вещества теплоту. По окончании процесса кристаллизации в равновесии будут находиться твердая и газообразная фазы. И если и дальше продолжать отнимать теплоту, то температура снова начнет понижаться. Соответственно уменьшается давление паров, находящихся в равновесии с кристаллической фазой. Точка, изображающая состояние вещества будет перемещаться вниз по фазовой диаграмме Т«Г.

Уравнение Клайперона-Клаузиуса для фазового превращения Т«Г имеет вид:

(4.5)

где r – теплота сублимации 1 моля твердого тела, V_Т - объем 1 моля твердого тела, V_Г - объем 1 моля газа (пара).

Поскольку V_Г> V_Т, то >0, т.е. фазовая диаграмма имеет вид возрастающей кривой. Далее в этом случае V_Г>> V_Т, и можно положить V_Г- V_Т» V_Г=V.

Из уравнения состояния идеального газа Þ .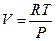

Тогда уравнение (4.5) примет вид:

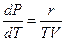или 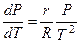. (4.6)

Это уравнение с разделяющими переменными:

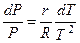. (4.7)

Решение уравнения (4.7) имеет вид:

,

или учитывая, что

,

, (4.8)

где e -энергия связи отдельного атома с кристаллом.

Вид фазовой диаграммы Р=Р (Т)для превращения Т«Г приведен на рис. 4.7. Как видно из рис. 4.7, все три фазовые диаграммы сходятся в одной точке (тройной точке А) и разбивают координатную плоскость на три области: область твердой фазы, область жидких состояний и область газообразных состояний вещества. Любая точка в одной из этих областей изображает соответствующее однофазное состояние вещества. Всякая точка, лежащая на одной из разграничивающих области кривых, изображает состояние равновесия двух соответствующих фаз вещества. Тройная точка изображает состояние равновесия всех трех фаз. Таким образом, каждая точка на диаграмме изображает определенное равновесное состояние вещества. Поэтому ее называют диаграммой состояния.

Для вещества с несколькими кристаллическими модификациями диаграмма состояния имеет более сложный характер. На рис. 4.8 изображена диаграмма для случая, когда число различных кристаллических модификаций равно двум. В этом случае имеются две тройные точки. В точке А в равновесии находятся жидкость, газ и первая кристаллическая модификация вещества, в точке А ¢ находятся в равновесии жидкость и обе кристаллические модификации.

Диаграмма состояния для каждого конкретного вещества строится на основе экспериментальных данных. Зная диаграмму состояния, можно предсказать, в каком состоянии будет находиться вещество при различных условиях (при различных значениях Р и Т), а также какие превращения будет претерпевать вещество при различных процессах.

Дата добавления: 2015-05-09