Двойственные задачи

Оптимальное решение задачи линейного программирования определяется теми значениями параметров модели, которые они имели в момент ее формирования и построения. В реальной экономике значения параметров, формирующих модель, с течением времени или под воздействием каких-либо обстоятельств могут меняться. В связи с этим особый интерес представляют методы, позволяющие определить изменения в оптимальном решении, обусловленные изменениями значений параметров модели. Одним из источников таких методов является теория двойственности, результаты которой позволяют также производить экономический анализ оптимальных решений экономико-математи-ческих моделей.

Каждой задаче линейного программирования соответствует задача, называемая двойственной или сопряженной по отношению к исходной задаче. Теория двойственности оказалась полезной для проведения качественных исследований задач линейного программирования.

Экономическая интерпретация двойственной задачи.

Рассмотрим задачу об использовании ресурсов.

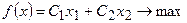
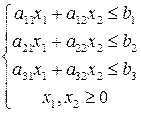
В этой модели: b_i – запас ресурса S_i, a_ij – число единиц ресурса S_i, потребляемого при производстве единицы продукции P_j, C_j – прибыль (выручка от реализации).

Предположим, что некоторая организация решила закупить ресурсы S₁, S₂ и S₃ предприятия и необходимо установить оптимальные цены на эти ресурсы: y₁,y₂ и y₃.

Очевидно, что покупающая организация заинтересована в том, чтобы затраты на все ресурсы в количествах b₁, b₂, b₃ по ценам y₁,y₂,y₃ были минимальными, то есть

Z(y)= b₁y₁ + b₂y₂ + b₃y₃ → min.

С другой стороны, предприятие, продающее ресурсы, заинтересовано в том, чтобы полученная выручка была не менее той суммы, которую предприятие могло получить при переработке ресурсов в готовую продукцию. На изготовление продукции P₁ расходуется a₁₁ ресурса S₁, a₂₁ ресурса S₂, а₃₁ ресурса S₃ 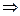a₁₁y₁ + a₂₁y₂ + a₃₁y₃ ≥ C₁. Аналогично для продукции P₂: a₁₂y₁ + a₂₂y₂ + a₃₂y₃ ≥ C₂. Также необходимо учесть, что цены на ресурсы (объективно обусловленные оценки) не могут быть отрицательными.

Объединяя все вышесказанное, получаем следующую экономико-математическая модель двойственной задачи:

Z(y)=b₁y₁ + b₂y₂ + b₃y₃ → min

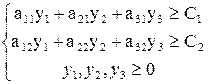
Цены ресурсов y₁, y₂, y₃ называются учетными, неявными, теневыми. Смысл этих названий состоит в том, что это условные, “ненастоящие” цены. В отличие от “внешних” цен C₁, C₂ на продукцию, известных, как правило, до начала производства, цены ресурсов y₁, y₂, y₃ являются внутренними, так как они задаются не извне, а определяются непосредственно в результате решения задачи, поэтому их часто называют оценками ресурсов.

Формулировка двойственной задачи

Найти такой набор оценок ресурсов, при которых общие затраты на ресурсы будут минимальными при условии, что затраты на ресурсы при производстве каждого вида продукции будут не менее выручки от реализации этой продукции.

Свойства взаимно двойственных задач

1. В одной задаче ищут максимум целевой функции, а в другой минимум.

2. Коэффициенты при переменных в целевой функции одной задачи являются свободными членами системы ограничений в другой.

3. Каждая из задач задана в стандартной форме, причем в задаче на максимум все неравенства вида ”≤”, а в задаче на минимум – все неравенства вида “≥”.

4. Матрицы коэффициентов при переменных в системах ограничений являются транспонированными друг к другу.

5. Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче.

6. Условия неотрицательности переменных имеются в обеих задачах.

Пример решения задачи.

Составить двойственную задачу для заданной.

Дана целевая функция f(x)= –х₁ + 2х₂ → max

И система ограничений: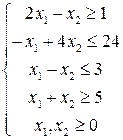

Приведем систему неравенств к правильному виду, чтобы все знаки неравенств соответствовали задаче на максимум:

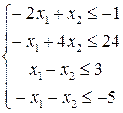
Тогда взаимно двойственная задача для исходной примет вид:

z(y)= – y₁+24y₂+3y₃-5y₄→min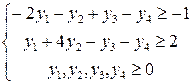

Запись решения двойственной задачи:

1) min z(y)=max f(x).

Если одна из задач имеет решение, то имеет решение и другая.

2) Установим соответствие между переменными: переменной x_i из исходной задачи ставится в соответствие дополнительная переменная из двойственной задачи, введенная в i-е ограничение (x₁ ~ y₅, x₂ ~ y₆). Аналогично, первоначальным переменным двойственной задачи соответствуют дополнительные переменные исходной задачи.

3) Компоненты оптимального решения двойственной задачи равны по абсолютной величине коэффициентам при соответствующих переменных в последней записи целевой функции исходной задачи.

4) Если в одной из двойственных задач нарушается единственность оптимального решения, то оптимальное решение двойственной задачи вырожденное.

Ø Важно помнить. Положительным (ненулевым) компонентам оптимального решения одной из взаимно двойственных задач соответствуют нулевые компоненты оптимального решения другой задачи. Таким образом, объективно обусловленные оценки ресурсов определяют степень дефицитности ресурсов: по оптимальному плану производства дефицитные (т.е. полностью использованные) ресурсы получают ненулевые оценки, а недефицитные – нулевые оценки.

Метод, при котором вначале симплексным методом решается двойственная задача, а затем оптимум и оптимальное решение исходной задачи находится с помощью теорем двойственности, называется двойственным симплексным методом. Его используют, когда решение двойственной задачи менее трудоемко (меньше число ограничений). Также с помощью решения двойственной задачи можно дать развернутую характеристику имеющимся на предприятии ресурсам и их использованию. Подробно об этом будет сказано позднее.

Пример решения задачи.. Последняя запись целевой функции исходной задачи с двумя переменными имела вид:

.

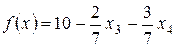Ее решение .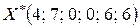

Поставим в соответствие переменные:

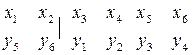
Под таблицей записываем по модулю коэффициенты из последней записи целевой функции исходной задачи.

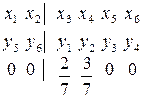
Следовательно, решение взаимно двойственной задачи будет иметь следующий вид: .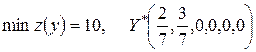

Чтобы лучше понять, почему дополнительные переменные одной задачи ставятся в соответствие первоначальным переменным другой задачи, представим их в виде таблицы, из которой видно, что они относятся к одинаковым экономическим понятиям.

Таблица 1.9

Компоненты оптимального решения исходной задачи
Число единиц продукции	Остатки ресурсов (число единиц)
Р1	Р2	S1	S2	S3	S4
x1	x2	x3	x4	x5	x6
y5	y6	y1	y2	y3	y4
Превышение затрат на ресурсы над ценой их реализации	Объективно обусловленные оценки ресурсов (условные цены)
Компоненты оптимального решения двойственной задачи

Ø Важно помнить. Если линейная функция одной из взаимно двойственных не ограничена, то условия другой задачи противоречивы.

Объективно обусловленные оценки ресурсов имеют и другой экономический смысл:

1) Они равны значениям частных производных линейной функции 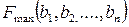по соответствующим аргументам, т. е.

.

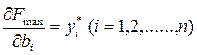Таким образом, оценки ресурсов показывают, на сколько денежных единиц изменится максимальная прибыль (выручка) от реализации продукции при изменении запаса соответствующего ресурса на одну единицу.

2) Двойственные оценки могут служить инструментом анализа и принятия правильных решений в условиях постоянно меняющегося производства. Так, например, с помощью объективно обусловленных оценок ресурсов возможно сопоставление оптимальных условных затрат и результатов производства.

Ø Важно помнить. Оценки ресурсов позволяют судить об эффекте не любых, а лишь сравнительно небольших изменений ресурсов. При резких изменениях сами оценки могут стать другими, что приведет к невозможности их использования для анализа эффективности производства.

3) По соотношениям объективно обусловленных оценок могут быть определены расчетные нормы заменяемости ресурсов, при соблюдении которых проводимые замены в пределах устойчивости двойственных оценок не влияют на эффективность оптимального плана.

Задания для самостоятельной работы.

1. Записать для задачи использования ресурсов взаимно двойственную и ее решение.

2. Дана задача линейного программирования, ее решение и последняя запись целевой функции. Записать для нее двойственную задачу и ее решение.

Экономико-математическая модель задачи:

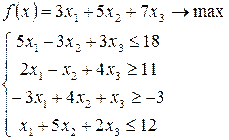
Последняя запись целевой функции: .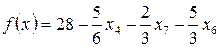

Ответ: .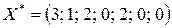

3. Для производства изделий А и В предприятие использует три вида сырья. Все необходимые для решения задачи данные приведены в таблице.

Таблица 1.10

Затраты ресурсов на производство изделий и их запасы

Вид сырья	А	В	Общее количество сырья на предприятии
I
II
III
Прибыль от реализации одного изделия

Решить задачу симплексным методом, составить к ней двойственную задачу и записать ее решение. Объяснить экономический смысл переменных, ограничений и целевой функции обеих задач.

4. Используя геометрическое решение двойственной задачи и теоремы двойственности, решить задачу линейного программирования.

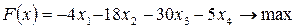
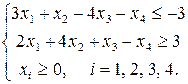
Дата добавления: 2015-05-09