Математическая модель сейсмограммы для однократно отраженных волн

Лекция 2

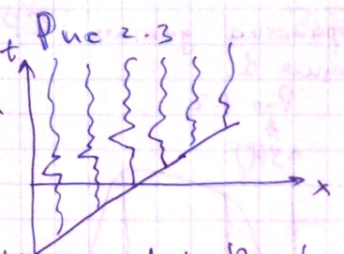
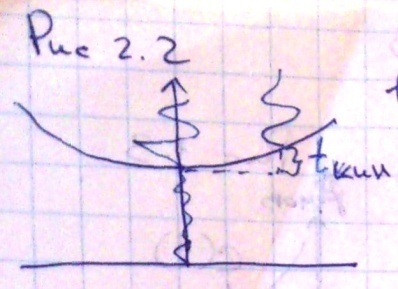Рис 2.2. С учетом этого при обработке данных в МОВ вводиться две координаты пространства x – пикет точки возбуждения, L – удаление ПП от ПВ. Рис 2.3. Соответственно условия возбуждения и приема также будут меняться в наборе трасс, входящих в сейсмограммы. Т.е. дополнительно в сейсмическую модель мы должны ввести некоторый коэффициент a_x(L), которая будет характеризовать неидентичность условий возбуждения и приема в пределах сейсмограммы. В этом случае можем написать 2.1. Кинематическая поправка рассчитывается по формуле 2.2.

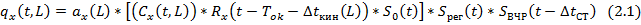
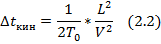
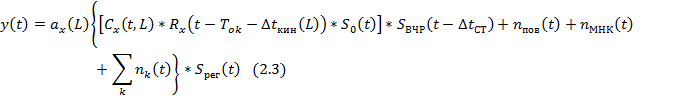
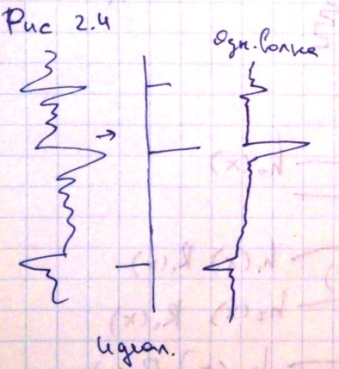Для всей сейсмограммы с помехами получим следующее выражение математической модели: 2.3. Здесь записаны все основные факторы, которые должны быть учтены при обработке. Основная цель обработки – устранить помехи и наилучшим образом выделить полезный сигнал. И поэтому при цифровой обработке нужно исключить все мешающие факторы и каждую сейсмическую трассу преобразовать (в идеальном случае) в импульсную трассу, рис 2.4. Также идеальный вариант получить только полезный сигнал однократной волны. После обработки мы должны получить сейсмическую трассу, которая может быть описана сверткой коэффициентов отражения и формы сигнала

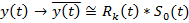
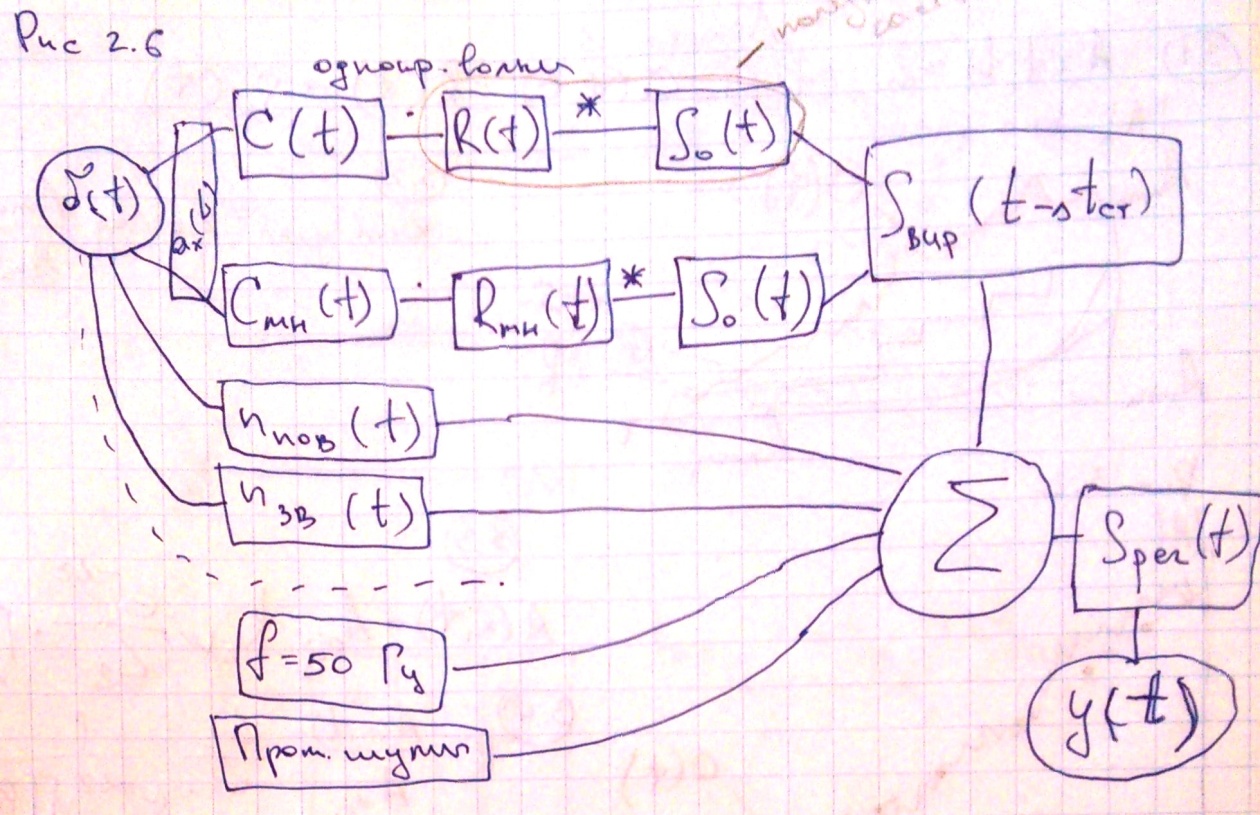
Блок-схема математической модели трассы, как канала связи

Считается, что в СР полевые сейсмические записи являются случайными функциями и каждая трасса – это некоторая реализация единого случайного процесса на данной площади. При обработке используется статистический подход, основанный на теории связи. И представляется, что в этом случае у нас имеется источник колебаний, которым чаще всего считается единичный импульс (импульс бесконечно большой амплитуды, интеграл от которого равен 1) δ(t), затем идет канал связи и регистрируемy(t), со всеми помехами. Рис 2.5. Регистрируемые функции должны быть стационарными и эргодическими.

Стационарность – это подобие статистических характеристик случайных функций. В СР под стационарностью понимают подобие статистических характеристик во времени. По идее сейсмическая трасса не является стационарной функцией. Чтобы ее привести к стационарной, как раз и нужно предусмотреть процедуру, которая устранит особенности сейсмических трасс. Таким образом, при цифровой обработке прежде всего следует сделать трассу стационарной, т.е. исключить коэффициент С(t) из сейсмических трасс.

Под эргодичностью обычно понимают подобие реализаций в пространстве, т.е. подобие статистических характеристик по осям x, у. В нашем случае для этого необходимо исключить неидентичность условий возбуждения и приема.

Под каналом связи подразумевается математическая схема для описания реальных процессов при прохождении полезной информации через канал связи с точки зрения статистических свойств этих процессов. На входе мы регистрируем случайную функцию, а на выходе – распределение вероятностей, преобразование проходящих через канал сигналов в выходные. Этот процесс должен отражать характер возможных искажений. Смысл создания математической модели состоит в формулировке математических связей между волновыми полями и искомыми параметрами среды.

Изобразим математическую модель как канал связи: рис 2.6. Предполагается, что при возбуждении колебаний у нас распространяется единичный импульс. Также могут возникать наводки от электрической сети, промышленные шумы. Также возникают поверхностные и звуковые волны. На все измерения влияет аппаратура.

Дата добавления: 2015-05-09