Принцип наименьшего действия в форме Якоби

Среди кинематически возможных движений системы, совершаемых между двумя положениями системы с одной и той же полной механической энергией, истинным будет то движение, для которого действие по Лагранжу имеет стационарное значение.

Задача. Рассмотрим движение точки по гладкой поверхности, если П=0. Действие по Мопертюи-Лагранжу 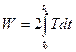= = 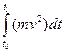mv²(t²-t¹).

Для действительного движения DW=0, т.е. mv²Dt=0.

Так как mv²/2 =h, то v=const и Dt=0.

По всем остальным путям движение происходит с постоянной скоростью, так как h= const.

Значит движение по прямому пути происходит с минимальным временем.

Задача (принцип Гамильтона).

Пусть материальная точка массой m брошена под углом a к горизонту в однородном поле силы тяжести с начальной скоростью v_o.

Решение. Траекторией точки будет парабола y = v₀sinat –1/2gt², x = v₀ cosat.

В момент времени 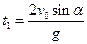точка, двигаясь по параболе, пересечет ось Ох.

В соответствии с принципом наименьшего действия Гамильтона время на прямом и окольных путях должно быть одинаковым. Для обоих движений П = mgz.

Для движения по параболе (на прямом пути)

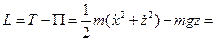
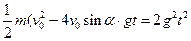и действие по Гамильтону

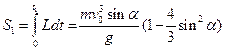(1)

Для прямолинейного движения (по окольному пути)

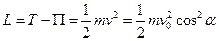и действие по Гамильтону

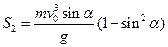(2)

При любом a величина (1) меньше величины (2), т.е., действие по Гамильтону на прямом (действительном) пути меньше, чем на окольном пути.

__________________________

Задача (принцип Мопертюи-Лагранжа).

Рассмотрим предыдущую задачу снова, чтобы представить яснее разницу между принципом Гамильтона и принципом Мопертюи-Лагранжа. Прямой путь представляет собой параболу. За окольный путь примем отрезок ОВ оси Ох. Угол считаем малым, так что прямой и окольный пути близки один к другому. Для обоих путей потенциальная энергия одинакова.

Так как полная механическая энергия должна быть одинакова для обоих путей, то и начальные скорости v₀ одинаковы.

Но если на прямом пути время определяется равенством 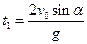, то для окольного пути оно будет иным и вычисляется по формуле .

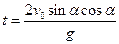Для движения по параболе кинетическая энергия равна

,

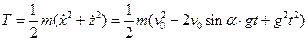Для прямолинейного движения кинетическая энергия равна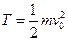

Действие по Мопертюи-Лагранжу для движения по параболе (по прямому пути)

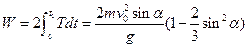(3)

Действие по Мопертюи-Лагранжу для прямолинейного движения (по окольному пути)

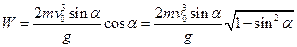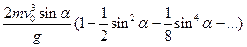= (4)

При достаточно малых значениях a величина (3) меньше величины (4), т.е., действие по Лагранжу на прямом пути меньше, чем на окольном.

-------------------------

Сравнение действий по Гамильтону и Лагранжу:

, , , .

--------------------------

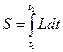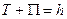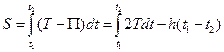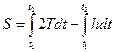
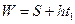
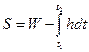
Введем в n-мерном координатном пространстве риманову метрику, определив элементарное расстояние между двумя соседними точками и выражением .

Если на систему наложены стационарные связи, то в этом случае кинетическая энергия системы является однородной квадратичной формой обобщенных скоростей

.

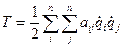Сопоставляя формулы, для кинетической энергии находим 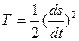, т.е. кинетическая энергия системы совпадает с кинетической энергии изображающей точки в n-мерном пространстве обобщенных координат, если массу точки принять равной единице.

В соответствии с законом сохранения энергии 2T = 2(h – П), тогда из выражения для кинетической энергии находим .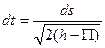

Если П=0, 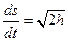, т.е. в этой метрике движение консервативной системы по инерции соответствует равномерному движению изображающей точки в координатном пространстве со скоростью .

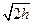Подставив полученное выражение в формулу 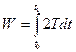, определяющую действие по Лагранжу, получим .

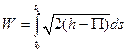Интеграл в этой форме называется действием по Якоби.

Дата добавления: 2015-05-09