Вывод канонических уравнений из принципа Гамильтона

Среди кинематически возможных движений голономной системы, совершаемых между двумя положениями системы с одной и той же полной механической энергией, истинным будет то движение, для которого действие по Якоби имеет стационарное значение.

Если П=0, то , где 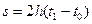- длина кривой, пройденной изображающей точкой за время . Из принципа Якоби следует, что 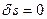, т.е. задача нахождения траектории свелась к задаче дифференциальной геометрии о нахождении геодезической линии в координатном пространстве с метрикой

Следовательно, движение голономной системы по инерции в пространстве обобщенных координат эквивалентно движению изображающей точки по геодезической линии этого пространства. Длина дуги геодезической линии меньше длины дуги любой другой линии, соединяющей заданные точки.

При движении механической системы в поле потенциальных сил в пространстве обобщенных координат вводится метрика 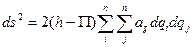(П<h).

Таким образом, движение голономной системы под действием потенциальных сил эквивалентно изображающей точки по инерции в пространстве Римана, метрика которого определена указанным выражением. Согласно принципу наименьшего действия в форме Якоби движение происходит по геодезической линии в римановом пространстве.

Примечание:

Кривизна поверхности инвариантная при изгибании и принадлежащая к внутренней геометрии поверхности называется геодезической кривизной. Геодезической линией на поверхности называется кривая, геодезическая кривизна которой в каждой точке равна нулю. Для того чтобы линия на поверхности была геодезической, необходимо и достаточно, чтобы проекция ее вектора кривизны на касательную плоскость равнялась нулю. Или: для того чтобы линия на поверхности была геодезической, необходимо и достаточно, чтобы ее главная нормаль во всех точках совпадала с нормалью к поверхности, или чтобы линия была прямой.

Функция Гамильтона , функция Лагранжа .

Из условия dS =0 следует 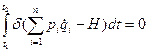, (1)

Так как 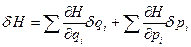и кроме того

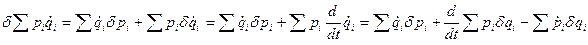
То соотношение принимает вид , (2)

ибо в силу закрепленности концов окольных путей. Несмотря на то, что q_i и p_i входят в функцию Гамильтона как независимые переменные, при вычислении интеграла (2) нельзя считать dq_i и dp_i независимыми, так как они связаны зависимостью, вытекающей из соотношения .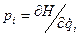

Но равенства . следуют из определения функции Гамильтона, поэтому в силу независимых вариаций dq_i обращаются в нуль и все множители при dq_i. Итак, получаем уравнения Гамильтона.

___________________________________________

Вывод уравнений Лагранжа второго рода из принципа Гамильтона .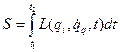

Из принципа следует

Используем свойство операторов: 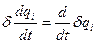. Тогда

,

.

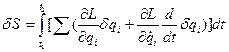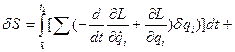
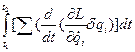В силу закрепленности концов , .

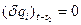второй интеграл в последнем выражении равен нулю. В самом деле

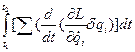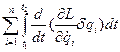= = =0

Таким образом, 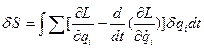и согласно принципу Гамильтона dS=0. Значит .

Вследствие произвольности интервала интегрирования .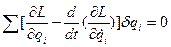

Так как вариации координат независимы, то получаем уравнения Лагранжа второго рода

.

_______________________________________________________

Дата добавления: 2015-05-09