Алгоритм Хаффмана

Алгоритм основан на том факте, что некоторые символы из стандартного 256-символьного набора в произвольном тексте могут встречаться чаще среднего периода повтора, а другие, соответственно, – реже. Следовательно, если для записи распространенных символов использовать короткие последовательности бит, длиной меньше 8, а для записи редких символов – длинные, то суммарный объем файла уменьшится.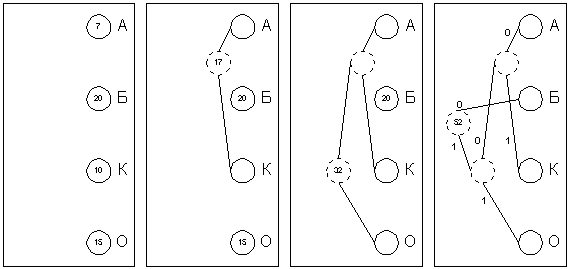

Хаффман предложил очень простой алгоритм определения того, какой символ необходимо кодировать каким кодом для получения файла с длиной, очень близкой к его энтропии (то есть информационной насыщенности). Пусть у нас имеется список всех символов, встречающихся в исходном тексте, причем известно количество появлений каждого символа в нем. Выпишем их вертикально в ряд в виде ячеек будущего графа по правому краю листа (рис. 1а). Выберем два символа с наименьшим количеством повторений в тексте (если три или большее число символов имеют одинаковые значения, выбираем любые два из них). Проведем от них линии влево к новой вершине графа и запишем в нее значение, равное сумме частот повторения каждого из объединяемых символов (рис.2б). Отныне не будем принимать во внимание при поиске наименьших частот повторения два объединенных узла (для этого сотрем числа в этих двух вершинах), но будем рассматривать новую вершину как полноценную ячейку с частотой появления, равной сумме частот появления двух соединившихся вершин. Будем повторять операцию объединения вершин до тех пор, пока не придем к одной вершине с числом (рис.2в и 2г). Для проверки: очевидно, что в ней будет записана длина кодируемого файла. Теперь расставим на двух ребрах графа, исходящих из каждой вершины, биты 0 и 1 произвольно – например, на каждом верхнем ребре 0, а на каждом нижнем – 1. Теперь для определения кода каждой конкретной буквы необходимо просто пройти от вершины дерева до нее, выписывая нули и единицы по маршруту следования. Для рисунка 4.5 символ "А" получает код "000", символ "Б" – код "01", символ "К" – код "001", а символ "О" – код "1".

В теории кодирования информации показывается, что код Хаффмана является префиксным, то есть код никакого символа не является началом кода какого-либо другого символа. Проверьте это на нашем примере. А из этого следует, что код Хаффмана однозначно восстановим получателем, даже если не сообщается длина кода каждого переданного символа. Получателю пересылают только дерево Хаффмана в компактном виде, а затем входная последовательность кодов символов декодируется им самостоятельно без какой-либо дополнительной информации. Например, при приеме "0100010100001" им сначала отделяется первый символ "Б": "01-00010100001", затем снова начиная с вершины дерева – "А" "01-000-10100001", затем аналогично декодируется вся запись "01-000-1-01-000-01" "БАОБАБ".

Дата добавления: 2015-05-07