
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Изучение свойств идеального газа на примере воздуха
|
|
|
|
ЛАБОРАТОРНАЯ РАБОТА № 2-1
Цель работы
- Экспериментальная проверка уравнения состояния идеального газа.
- Определение температуры абсолютного нуля по шкале Цельсия.
Теоретические основы лабораторной работы
Часть 1
В том случае, когда состояние газа далеко от области фазовых превращений, его с достаточной степенью точности можно считать идеальным. В качестве идеального газа в работе используется обычный атмосферный воздух.
Для произвольной массы m идеального газа справедливо следующее уравнение состояния
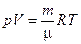 , (1)
, (1)
где p – давление, V – объем,  – молярная масса, T – абсолютная температура газа, R – универсальная газовая постоянная. Это уравнение называется уравнением Менделеева-Клапейрона.
– молярная масса, T – абсолютная температура газа, R – универсальная газовая постоянная. Это уравнение называется уравнением Менделеева-Клапейрона.
Нулю абсолютной температуры по шкале Цельсия соответствует значение 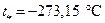 . Градусы шкалы абсолютной температуры (шкалы Кельвина) и шкалы Цельсия выбраны одинаковыми. Поэтому значение абсолютной температуры связано со значением температуры по шкале Цельсия формулой
. Градусы шкалы абсолютной температуры (шкалы Кельвина) и шкалы Цельсия выбраны одинаковыми. Поэтому значение абсолютной температуры связано со значением температуры по шкале Цельсия формулой
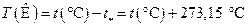 . (2)
. (2)
Пусть исследуемый газ находиться в цилиндре с контролируемым рабочим объемом V ц (см. рис. 1), масса газа в цилиндре m ц. Температура t цилиндра с газом поддерживается постоянной.
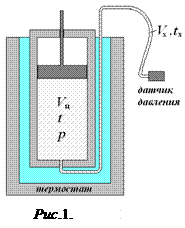 Датчик давления, работающий при комнатной температуре, вынесен за пределы рабочего объема и соединен с последним трубкой. Объем газа V х в этой трубке мал по сравнению с рабочим объемом V ц. В соединительной трубке также находится газ массой m x при некоторой неизвестной средней температуре t х, лежащей в интервале от комнатной температуры до температуры t рабочего объема.
Датчик давления, работающий при комнатной температуре, вынесен за пределы рабочего объема и соединен с последним трубкой. Объем газа V х в этой трубке мал по сравнению с рабочим объемом V ц. В соединительной трубке также находится газ массой m x при некоторой неизвестной средней температуре t х, лежащей в интервале от комнатной температуры до температуры t рабочего объема.
В работе измеряется зависимость давления p газа от величины рабочего объема V ц при разных значениях температуры t (от 20°С до 60°С). Выведем соотношение, связывающее рабочий объем и давление газа при постоянной температуре. Общее количество вещества в рабочем объеме и соединительной трубке
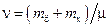 (3)
(3)
в течение всей работы остается постоянным. Выражая массы газа m ц и m x из уравнения состояния (1), абсолютную температуру из соотношения (2), и подставляя найденные выражения в формулу (3), получим
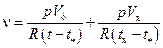 . (4)
. (4)
Из этого уравнения найдем искомое соотношение:
 . (5)
. (5)
Из-за перераспределения газа между объемами V ц и V х в процессе измерения температура t х может изменяться. Однако, при относительно малой величине V х изменением второго слагаемого в формуле (5) можно пренебречь. Поэтому при неизменной температуре t зависимость рабочего объема V ц от обратного давления 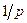 является линейной. Угловой коэффициент этой зависимости
является линейной. Угловой коэффициент этой зависимости
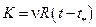 , (6)
, (6)
в свою очередь, линейно меняется с температурой и обращается в нуль при абсолютном нуле температур. Таким образом, изучение зависимости 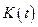 позволяет найти значение
позволяет найти значение 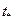 .
.
Рассмотрим другой, более точный, способ определения величины 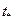 . Если для разных температур измерение давления проводить при одних и тех же значениях объема, то полученные данные легко преобразуются в зависимость давления от температуры при разных значениях рабочего объема газа. Теоретический вид этой зависимости получается из уравнения (5):
. Если для разных температур измерение давления проводить при одних и тех же значениях объема, то полученные данные легко преобразуются в зависимость давления от температуры при разных значениях рабочего объема газа. Теоретический вид этой зависимости получается из уравнения (5):
 , (7)
, (7)
где  . Справедливость приближенного равенства в формуле (7) обусловлена тем, что значения функции
. Справедливость приближенного равенства в формуле (7) обусловлена тем, что значения функции 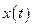 малы, и для малых x можно воспользоваться формулой приближенных вычислений:
малы, и для малых x можно воспользоваться формулой приближенных вычислений:
 . (8)
. (8)
В данном случае  .
.
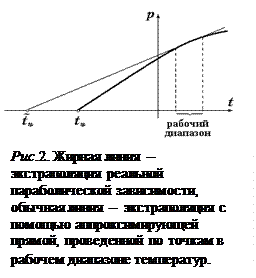 При неизменном рабочем объеме V ц график зависимости давления от температуры в соответствии с формулой (7) должен быть почти линейным. Причем давление должно обращаться в нуль как раз при
При неизменном рабочем объеме V ц график зависимости давления от температуры в соответствии с формулой (7) должен быть почти линейным. Причем давление должно обращаться в нуль как раз при  . Из-за малости функции
. Из-за малости функции 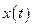 отклонение от линейности невелико, и при измерении в ограниченном диапазоне температур практически незаметно. Но, если искать значение
отклонение от линейности невелико, и при измерении в ограниченном диапазоне температур практически незаметно. Но, если искать значение  с помощью линейной аппроксимации экспериментальной зависимости
с помощью линейной аппроксимации экспериментальной зависимости  , продолжая (экстраполируя) аппроксимирующую прямую до пересечения с осью t, то найденное приближенное значение
, продолжая (экстраполируя) аппроксимирующую прямую до пересечения с осью t, то найденное приближенное значение  окажется систематически смещенным влево относительно истинного значения
окажется систематически смещенным влево относительно истинного значения 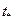 (см. рис. 2). Причина этого в следующем. Величина
(см. рис. 2). Причина этого в следующем. Величина 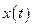 в первом приближении линейно растущая функция температуры, с учетом этого график функции
в первом приближении линейно растущая функция температуры, с учетом этого график функции  из уравнения (7) оказывается параболой выпуклой вверх. Аппроксимирующая прямая, параметры которой найдены по точкам в рабочем диапазоне температур, идет практически по касательной к этому графику, «промахиваясь» мимо истинного значения
из уравнения (7) оказывается параболой выпуклой вверх. Аппроксимирующая прямая, параметры которой найдены по точкам в рабочем диапазоне температур, идет практически по касательной к этому графику, «промахиваясь» мимо истинного значения  , как изображено на рис. 1. Однако, можно показать, что разность
, как изображено на рис. 1. Однако, можно показать, что разность  при малом отношении
при малом отношении  должна убывать обратно пропорционально объему V ц. Поэтому, правильное значение температуры абсолютного нуля может быть найдено как предел:
должна убывать обратно пропорционально объему V ц. Поэтому, правильное значение температуры абсолютного нуля может быть найдено как предел:
 , (9)
, (9)
линейным продолжением графика зависимости 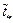 от
от  к значению
к значению 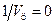 .
.
Описание установки
Общий вид лабораторной установки показан на рисунке 3. Исследуемый газ находится под поршнем в цилиндре 1, закрепленном на опорной площадке 2. Шток поршня имеет винтовую нарезку и вставлен в гайку, также закрепленную на опорной площадке. Гайка удерживает шток в заданном положении и с ее помощью осуществляется преобразование вращения штока в поступательное перемещение поршня (один оборот маховика штока соответствует изменению объема на 5 мл). Рабочий объем цилиндра определяется по шкале на цилиндре. Если шкала не видна, то изменение объема от некоторого заданного значения можно определить, отсчитывая обороты маховика штока.
Роль термостата 3 выполняет металлический термос, заполняемый водой разной температуры, в которую погружается цилиндр 1. Измерение температуры производится с помощью датчика температуры закрепленного на конце щупа 4, погружаемого вместе с цилиндром в термостат. Давление измеряется манометрическим дифференциальным датчиком 5, который закреплен на стенде 6, и соединяется трубкой с рабочим объемом. С помощью преобразователя сигналов 7 датчики соединяются с цифровым измерительным прибором 8. Прибор показывает текущую температуру t (в градусах Цельсия) датчика температуры и разность 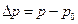 (в килопаскалях) между давлением p газа в рабочем объеме и давлением
(в килопаскалях) между давлением p газа в рабочем объеме и давлением 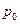 окружающего воздуха в лаборатории.
окружающего воздуха в лаборатории.
 Исходно в термостате находится вода комнатной температуры. Отливая холодную и добавляя горячую воду, можно изменять рабочую температуру термостата. Для переливания воды используется пластиковая кружка 9. Для уменьшения вероятности попадания воды на рабочий стол воду переливают над поддоном 10, на который также ставится термостат во время проведения измерений. Для перемешивания воды в термостате используется лопатка 11. Рядом с каждыми двумя установками имеется емкость для использованной воды и электрический чайник с горячей водой.
Исходно в термостате находится вода комнатной температуры. Отливая холодную и добавляя горячую воду, можно изменять рабочую температуру термостата. Для переливания воды используется пластиковая кружка 9. Для уменьшения вероятности попадания воды на рабочий стол воду переливают над поддоном 10, на который также ставится термостат во время проведения измерений. Для перемешивания воды в термостате используется лопатка 11. Рядом с каждыми двумя установками имеется емкость для использованной воды и электрический чайник с горячей водой.
Порядок выполнения работы
1. С помощью лабораторного барометра определить текущее атмосферное давление 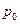 и записать его значение в протокол работы.
и записать его значение в протокол работы.
2. Включить цифровой измерительный прибор в режиме измерения температуры и давления (включение производит дежурный инженер). Установить рабочий объем цилиндра 100 мл (обратите внимание на положение визирной стрелки на маховике штока поршня). Залить в термостат четыре с половиной кружки воды комнатной температуры. Аккуратно поместить в термостат цилиндр 1 с датчиком температуры так, чтобы опорная площадка цилиндра легла на горлышко термостата.
3. Подождать пока показания давления престанут изменяться (приблизительно 5–10 минут). При этом рабочий объем газ придет в тепловое равновесие с термостатом. Записать значение 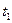 температуры термостата (около 20 °C) в таблицу 1.1. Последовательно изменяя рабочий объем газа с шагом 10 мл сначала в сторону уменьшения до 48,5 мл, затем в сторону увеличения до 142,5 мл и обратно до 100 мл, дважды измерить разность давлений
температуры термостата (около 20 °C) в таблицу 1.1. Последовательно изменяя рабочий объем газа с шагом 10 мл сначала в сторону уменьшения до 48,5 мл, затем в сторону увеличения до 142,5 мл и обратно до 100 мл, дважды измерить разность давлений 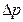 для каждого значения
для каждого значения  в таблице. 1.1. Результаты заносятся в ячейки третьего и четвертого столбцов таблицы по часовой стрелке. Изменение объема можно контролировать, не вынимая цилиндр из термостата – уменьшению на 10 мл соответствует два оборота маховика по часовой стрелке.
в таблице. 1.1. Результаты заносятся в ячейки третьего и четвертого столбцов таблицы по часовой стрелке. Изменение объема можно контролировать, не вынимая цилиндр из термостата – уменьшению на 10 мл соответствует два оборота маховика по часовой стрелке.
Таблица 1.1. Зависимость давления от объема при температуре 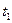 =….
=….
| № п.п. |  , мл , мл
| 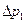 , кПа , кПа
| 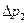 , кПа , кПа
| 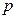 , кПа , кПа
| 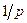 , кПа–1 , кПа–1
|
Приборные погрешности:  = 1 мл,
= 1 мл, 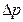 = 0,1 кПа.
= 0,1 кПа.
4. Аккуратно вынуть рабочий цилиндр с датчиком температуры из термостата, положить на поддон. Отлить из термостата приблизительно три четверти кружки воды. Вылить воду из кружки в емкость для использованной воды. Налить из чайника три четверти кружки горячей воды в термостат. Перемешать воду в термосе. Поместить в термостат цилиндр с датчиком температуры. В термостате должна установиться новая температура 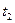 (около 30 °C). Повторить измерения п.3. Занести результаты в таблицу 1.2, аналогичную таблице 1.1.
(около 30 °C). Повторить измерения п.3. Занести результаты в таблицу 1.2, аналогичную таблице 1.1.
5. Последовательно изменяя температуру термостата до значений  (
(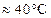 ),
),  (
( )
) 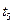 (
( ), как описано в п.4, записать получившиеся значения температур и произвести измерения п.3. Занести результаты в таблицы 1.3, 1.4, 1.5, аналогичные таблице 1.1.
), как описано в п.4, записать получившиеся значения температур и произвести измерения п.3. Занести результаты в таблицы 1.3, 1.4, 1.5, аналогичные таблице 1.1.
6. После выполнения всех измерений выключить цифровой измерительный прибор, вынуть цилиндр с датчиком температуры и положить на поддон. Вылить воду из термостата в емкость для использованной воды.
Обработка результатов измерений
1. Перевести показания лабораторного барометра из миллиметров ртутного столба в паскали:
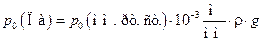 . (10)
. (10)
Здесь  – плотность ртути,
– плотность ртути,  – ускорение свободного падения на широте Санкт-Петербурга.
– ускорение свободного падения на широте Санкт-Петербурга.
2. Для каждой из таблиц 1.1 – 1.5 вычислить давление газа 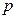 по формуле
по формуле
 , (11)
, (11)
обратное давление 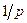 и заполнить пятую и шестую колонки таблиц.
и заполнить пятую и шестую колонки таблиц.
3. По данным таблиц 1.1 – 1.5 для температур  построить на одной координатной сетке графики зависимости рабочего объема
построить на одной координатной сетке графики зависимости рабочего объема  от обратного давления
от обратного давления 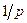 . Убедится, что зависимость
. Убедится, что зависимость  от
от 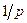 во всех пяти случаях является прямолинейной.
во всех пяти случаях является прямолинейной.
4. Перенести значения рабочих температур  во второй столбец таблицы 2.1. Для каждого из графиков
во второй столбец таблицы 2.1. Для каждого из графиков  от
от 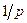 рассчитать угловой коэффициент
рассчитать угловой коэффициент  по формулам, приведенным в дополнении к работе. Значения
по формулам, приведенным в дополнении к работе. Значения  также занести в таблицу.
также занести в таблицу.
Таблица 2.1. Зависимость углового коэффициента графика  (
(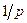 ) от температуры газа.
) от температуры газа.
| № п.п. |  , °С , °С
|  , Дж , Дж
|
- По таблице 2.1. построить график зависимости
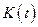 . Как следует из формулы (6) этот график должен «идти» прямолинейно и пересекать ось
. Как следует из формулы (6) этот график должен «идти» прямолинейно и пересекать ось  при температуре абсолютного нуля. По найденным экспериментальным точкам найти угловой коэффициент
при температуре абсолютного нуля. По найденным экспериментальным точкам найти угловой коэффициент  и свободное слагаемое
и свободное слагаемое  для зависимости
для зависимости 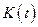 по формулам (16), (17). Рассчитать температуру абсолютного нуля:
по формулам (16), (17). Рассчитать температуру абсолютного нуля:
 . (12)
. (12)
По формулам (18), (19) найти погрешности 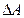 ,
, 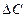 и вычислить погрешность температуры абсолютного нуля:
и вычислить погрешность температуры абсолютного нуля:
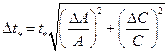 . (13)
. (13)
- По данным таблиц 1.1 – 1.5 заполнить таблицу 2.2.
Таблица 2.2. Зависимость давления газа от температуры при разных значениях объема.
 , мл , мл
| ||||||||||
 , С , С
| 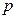 , кПа , кПа
| |||||||||
 , мл–1 , мл–1
| ||||||||||
 , С , С
|
Пользуясь таблицей 2.2 для значений объема цилиндра 50, 90, 140 мл на одной координатной сетке построить графики  , убедится, что они «идут» прямолинейно.
, убедится, что они «идут» прямолинейно.
- Для каждого из объемов в таблице 2.2 найти значение обратного объема
 и рассчитать величину
и рассчитать величину 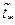 по формуле
по формуле
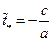 , (14)
, (14)
где 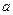 и
и 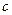 , соответственно, угловой коэффициент и свободное слагаемое для зависимости
, соответственно, угловой коэффициент и свободное слагаемое для зависимости 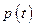 , вычисляемые по формулам (16), (17). Занести значения в таблицу 2.2.
, вычисляемые по формулам (16), (17). Занести значения в таблицу 2.2.
- Пользуясь таблицей 2.2, по формулам (16), (17) найти угловой коэффициент
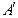 и свободное слагаемое
и свободное слагаемое  для зависимости
для зависимости  . Величина
. Величина  фактически есть предел (9), т.е. совпадает со значением
фактически есть предел (9), т.е. совпадает со значением  . На координатной сетке
. На координатной сетке 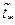 от
от  отметить экспериментальные точки и начертить прямую, соответствующую найденным параметрам
отметить экспериментальные точки и начертить прямую, соответствующую найденным параметрам 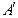 и
и  . Продолжить прямую до пересечения с осью ординат.
. Продолжить прямую до пересечения с осью ординат. - Рассчитать погрешность
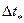 как
как 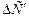 по формулам (18)–(19).
по формулам (18)–(19).
Дополнение. Вычисление наиболее вероятных параметров прямой линии
(по методу наименьших квадратов)
Пусть 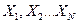 – абсциссы,
– абсциссы,  – ординаты графика некоторой экспериментально измеренной зависимости
– ординаты графика некоторой экспериментально измеренной зависимости  . Если предполагается, что эта зависимость линейна, т.е.
. Если предполагается, что эта зависимость линейна, т.е.  , то наиболее вероятные значения углового коэффициента
, то наиболее вероятные значения углового коэффициента  и свободного слагаемого
и свободного слагаемого  можно найти из требования минимальности суммы квадратов отклонений ординат экспериментальных точек от искомой прямой:
можно найти из требования минимальности суммы квадратов отклонений ординат экспериментальных точек от искомой прямой:
 . (15)
. (15)
Исходя из условия (15) можно получить следующие выражения
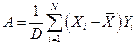 ,
, 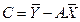 , (16)
, (16)
где
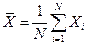 ,
,  ,
,  . (17)
. (17)
Погрешности коэффициента и слагаемого вычисляются по формулам
 ,
,  , (18)
, (18)
где
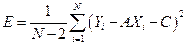 . (19)
. (19)
Вычисления удобно проводить с помощью какого-нибудь математического пакета или электронных таблиц, например Microsoft Excel.
|
|
|
|
Дата добавления: 2015-05-09; Просмотров: 1390; Нарушение авторских прав?; Мы поможем в написании вашей работы!