Динамический режим систем [7, 8, 9]

Установившийся режим не является характерным для системы. Обычно на управляемый процесс действуют различные возмущения, отклоняющие управляемый параметр от заданной величины. Процесс установления требуемого значения управляемой величины называется регулированием. Ввиду инерционности звеньев регулирование не может осуществляться мгновенно.

Рис. 2.3.1.

Переходные процессы в системе. Допустим, система находится в установившемся режиме, и имеет значение выходной величины y = y₀. Пусть в момент t = 0 на объект воздействовал какой-либо возмущающий фактор, отклонив значение регулируемой величины от номинальной. Через некоторое время (рис. 2.3.1) регулятор вернет систему к первоначальному состоянию (с учетом статистической ошибки). Если этот переходной процесс происходит по апериодическому временному закону, то процесс регулирования называется апериодическим. При резких возмущениях в системах возможен также колебательный затухающий процесс, а в неустойчивых системах - возникновение незатухающих колебаний и расходящийся колебательный процесс.

Таким образом, основным режимом работы систем считается динамический режим, характеризующийся протеканием в ней определенных переходных процессов.

Поведение системы или любого ее звена в динамических режимах описывается уравнением временной динамики y(t) = F(u,f,t). Как правило, это дифференциальное уравнение или система дифференциальных уравнений. Поэтому основным методом исследования систем в динамических режимах является метод решения дифференциальных уравнений. Порядок дифференциальных уравнений может быть довольно высоким, и определенной зависимостью могут быть связаны как входные и выходные величины u(t), f(t), y(t), так и скорости их изменения, ускорения и т.д. Поэтому уравнение динамики в общем виде можно записать так:

F(y, y', y'',..., y⁽ⁿ⁾, u, u', u'',..., u^(m), f, f ', f '',..., f^(k)) = 0.

Существует два способа получения дифференциальных уравнений (ДУ) объекта:

· Способ применения известных законов (закон Ома, законы механики и т.д.). Способ применим в случаях, когда объект управления простой и система невысокого порядка, или когда объект очень сложный, но можно воспользоваться законами статистики.

· Эвристический способ. Используются уравнения, основанные на опыте работы с предыдущими объектами, экспертные оценки, мнение специалистов. Такое описание называют феноменологическим, т.е. описанием объекта по основным чертам его внешнего поведения, без глубокого формального (математического, физического и т.п.) проникновения в сущность его функционирования.

Для полученной модели должны быть исследованы:

1. адекватность модели поведению реального объекта;

2. границы адекватности по пределам изменения параметров и переменных модели.

Линеаризация уравнения динамики. В общем случае уравнение динамики оказывается нелинейным. В целях упрощения нелинейные уравнения заменяют линейными, которые приблизительно (с определенной точностью) описывают динамические процессы в системе.

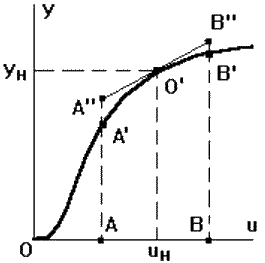Рис. 2.3.2.

В основе линеаризации нелинейных уравнений лежит допущение, что в нормально функционирующей системе отклонения регулируемой величины и переменных процесса от стационарных (установившихся) значений представляют собой достаточно малые величины. Это положение, как правило, всегда действительно для замкнутых систем. В пределах малых отклонений нелинейные зависимости между величинами, входящими в уравнение динамики, могут быть приближенно представлены отрезками прямых линий. Например, нелинейная статическая характеристика звена на участке АВ (рис. 2.3.2) может быть представлена отрезком касательной А"В" в точке номинального режима. Начало координат переносится в точку О', и в уравнениях записываются не абсолютные значения величин y, u, f, а их отклонения от номинальных значений: Dy = y-у_н, Du = u-u_н, Df = f-f_н. Это позволяет получить нулевые начальные условия, если считать, что при t ≤ 0 система находилась в номинальном режиме.

Математическое обоснование линеаризации состоит в том, что если известно значение f(a) какой - либо функции f(x) в любой точке x = a, а также значения производных от этой функции в данной точке f '(a), f ''(a),..., f⁽ⁿ⁾(a), то в любой другой достаточно близкой точке x+Dx значение функции можно определить, разложив ее в окрестности точки a в ряд Тейлора:

Аналогично можно разложить и функцию нескольких переменных. Для простоты возьмем упрощенный, но наиболее характерный вариант уравнения динамики систем: F(y,y',y",u,u') = f. Здесь производные по времени u',y',y" также являются переменными. В точке, близкой к номинальному режиму: f = f_н+Df и F = F_н+DF. Разложим функцию F в ряд Тейлора в окрестности точки номинального режима, отбрасывая члены ряда высоких порядков малости:

.

В номинальном режиме имеем частное решение F_н = f_н, а все частные производные функции F в точке O' представляют собой некоторые постоянные коэффициенты, или переменные во времени, если функция F содержит переменную t в явном виде. Заменяя значения частных производных соответствующими коэффициентами и переходя от приращений переменных к их производным, получаем:

A₀ y'' + A₁ y' + A₂ y = B₀ u' + B₁ u + f.

В данном уравнении используются не абсолютные значения величин y, u, f и их производных по времени, а отклонения этих величин от номинальных значений. Поэтому полученное уравнение называют уравнением в отклонениях.

В общем случае частные производные представляют собой либо постоянные матрицы зависимости от внешних воздействий f, значения которых могут быть существенно нелинейными, либо матрицы, зависящие только от времени, и полученное уравнение есть либо система линейных дифференциальных уравнений с постоянными коэффициентами относительно отклонений y и u, либо система с переменными коэффициентами, которые и решаются относительно выходной величины. Порядок системы уравнений равен n по порядку производной при y.

Для дифференциального уравнения произвольного порядка:

A₀ y⁽ⁿ⁾ + A₁ y^(n-1) +... + A_n-1 y' + A_n y = B₀ u^(m) +... + B_m-1 u' + B_m u + f.

Рис. 2.3.3.

К частным производным линеаризованной системы можно применить принцип суперпозиции: реакция системы на несколько одновременно действующих входных воздействий равна сумме реакций на каждое воздействие в отдельности. Это позволяет звено с двумя входами u и f разложить на два звена, каждое из которых имеет один вход и один выход (рис. 2.3.3). Поэтому в дальнейшем мы ограничимся изучением поведения систем и звеньев с одним входом, уравнение динамики которых имеет вид:

a₀ y⁽ⁿ⁾ + a₁ y^(n-1) +... + a_n-1 y' + a_n y = b₀ u^(m) +... + b_m-1 u' + b_m u.

Это уравнение описывает систему в динамическом режиме лишь приближенно с той точностью, которую обеспечивает линеаризация. Обычно n ≥ m, так как при n < m системы технически нереализуемы.

Передаточная функция. В теории управления часто используют символическую операторную форму записи дифференциальных уравнений. При этом вводится понятие алгебраизированного оператора дифференцирования p = d/dt так, что, dy/dt = py, а pⁿ = dⁿ /dtⁿ. Это лишь другое сокращенное обозначение операции дифференцирования. Соответственно, операция интегрирования записывается как 1/p. В операторной форме исходное дифференциальное уравнение записывается как алгебраическое:

a₀p⁽ⁿ⁾y+a₁p^(n-1)y+...+a_ny = (a₀p⁽ⁿ⁾+a₁p^(n-1)+...+ a_n)y = (b₀p^(m)+...+b_m-1p+b_m)u.

Не надо путать эту форму записи с операционным исчислением, здесь используются непосредственно функции y(t), u(t) (оригиналы), а не их изображения Y(p), U(p), получаемые из оригиналов преобразованием Лапласа. При нулевых начальных условиях с точностью до обозначений записи действительно похожи, и некоторые правила операционного исчисления применимы к операторной форме записи уравнений динамики. Так, оператор р можно выносить за скобки и можно рассматривать в качестве сомножителя, но без права перестановки: py ≠ yp. Условно можно считать оператор р алгебраической величиной.

Уравнение динамики в операторной форме:

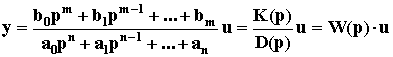
Дифференциальный оператор W(p) называют передаточной функцией. Она определяет зависимость отношения выходной величины звена к входной во времени: W(p) = y(t)/u(t), т.е. динамический коэффициент усиления. Передаточные функции в операторной форме также представляют собой сокращенную символическую запись дифференциальных уравнений. В установившемся режиме d/dt = 0, p = 0, и передаточная функция превращается в коэффициент передачи звена K = b_m /a_n.

Знаменатель передаточной функции D(p) = a₀pⁿ+a₁p^n-1+a₂p^{n -2}+...+a_n называют характеристическим полиномом. Его корни, при которых знаменатель D(p) обращается в ноль, а W(p) стремится к бесконечности, называются полюсами передаточной функцией.

Числитель K(p) = b₀p^m+b₁p^m-1+...+b_m называют операторным коэффициентом передачи. Его корни, при K(p) = 0 и W(p) = 0, называются нулями передаточной функции.

Звено системы с известной передаточной функцией называют динамическим звеном. Под динамическим звеном понимают устройство любого физического вида и конструктивного оформления, описываемое определенным дифференциальным уравнением. На схемах динамическое звено изображают прямоугольником, внутри которого записывается выражение передаточной функции. Для звена с двумя входами и одним выходом (рис. 2.3.3) должны быть записаны передаточные функции по каждому из входов. Передаточная функция является основной характеристикой звена, из которой можно получить все остальные характеристики. Она определяется только параметрами системы и не зависит от входных и выходных величин. Например, одним из динамических звеньев является интегратор. Его передаточная функция W_и(p) = 1/p. Схема системы, составленная из динамических звеньев, называется структурной.

Элементарные динамические звенья. Динамика большинства функциональных элементов систем независимо от исполнения может быть описана одинаковыми по форме дифференциальными уравнениями не более второго порядка. Такие элементы называют элементарными динамическими звеньями. Элементарные динамические звенья имеют один вход и один выход, а передаточная функция элементарного звена задается отношением двух полиномов:

W_э(p) = (b₀p² + b₁p + b₂) / (a₀p² + a₁p + a₂).

Известно также, что любой полином произвольного порядка можно разложить на простые сомножители:

D(p) = a₀p⁽ⁿ⁾ + a₁p^(n-1) +...+a_n = a₀ (p-p₁) (p-p₂)...(p-p_n),

где p₁, p₂,..., p_n - корни полинома D(p). Аналогично:

K(p) = b₀p^(m)+...+ b_m-1p+b_m = b₀ (p-p^~₁) (p-p^~₂)...(p-p^~_m),

где p^~₁, p^~₂,..., p^~_m - нули полинома K(p). Отсюда:

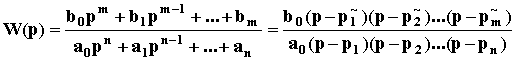
Корни любого полинома могут быть либо вещественными, либо комплексными попарно сопряженными. Пара комплексно сопряженных корней соответствует полиному второй степени. Передаточную функцию линеаризованной системы можно представить как произведение передаточных функций элементарных звеньев:

W = K W₁ W₂ W₃ …,

где К=b₀/a₀ – множитель, которым может регулироваться общая чувствительность системы к управляющим или дестабилизирующим воздействиям. Каждому такому звену в системе, как правило, соответствует отдельный узел. Зная свойства отдельных звеньев можно судить о динамике системы в целом.

Классификация звеньев производится по виду их дифференциальных уравнений и соответствующих передаточных функций, независимо от исполнения (механические, гидравлические, электрические и пр.). Передаточные функции типовых звеньев, из которых синтезируются системы, обычно имеют числитель или знаменатель, равный единице.

Дата добавления: 2015-05-09