Решение

Исследование свойств САУ в пакете MATLAB

Copyright ©2008 Davydov А.V.

Литература

1. Гайдук А.Р., Беляев В.Е., Пьявченко Т.А. Теория автоматического управления в примерах и задачах с решениями в MATLAB: Учебное пособие. 2-е изд., испр. – Спб.: Издательство «Лань», 2011 – 464 с.: ил. – (Учебники для вузов. Специальная литература).

2. Электронные файлы лекций Пьявченко Т.А. по ТАУ в цифровом кампусе ЮФУ.

Задание. Исследовать систему автоматического управления (САУ) с заданной передаточной функцией в разомкнутом состоянии и главной единичной отрицательной ОС. Исследование заключается в анализе показателей качества переходных и вынужденных (установившихся) режимов. Передаточная функция разомкнутой системы выбирается по варианту, который соответствует номеру списочного состава группы (см. приложение 1).

Задание необходимо выполнять, воспользовавшись пакетом MATLAB и произведя следующие действия:

1. Функцией BODE оценить устойчивость и, если система устойчива, – запасы устойчивости по фазе и по модулю.

2. Построить годограф Найквиста, по которому также сделать заключение об устойчивости системы.

3. В пакете Editor получить реакцию системы на скачок 1(t). По полученной переходной функции оценить показатели качества переходного процесса.

4. Если САУ устойчива, оценить точность системы на регулярный сигнал вида.

5. По полученным в п. 1-4 результатам сделать заключение о характере поведения системы с заданной передаточной функцией.

6. Найти предельный коэффициент передачи Kкр системы и проверить по частотным и временным характеристикам на соответствие критическому режиму.

7. Изменить коэффициент передачи K так, чтобы новые запасы устойчивости обеспечивали апериодический переходный процесс, если это возможно изменением только К без ввода дополнительной коррекции.

8. В пакете SIMULINK создать структурную модель системы и получить её временные характеристики.

9. Сделать полный вывод о показателях качества процесса управления заданной системы.

Все перечисленные выше действия покажем для САУ, к примеру имеющей в разомкнутом состоянии следующую передаточную функцию

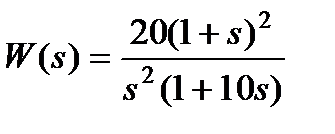(1)

Для детального исследования САУ представим её в виде структурной схемы, изображенной на рис. 1, в соответствии с которым передаточная функция (1) является последовательным соединением отдельных звеньев: 1) интегрирующего усилителя с форсирующим звеном ,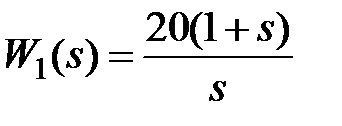

2) инерционно-форсирующего звена ,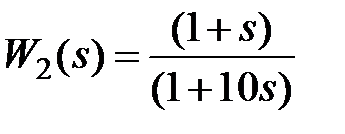

3) интегрирующего звена .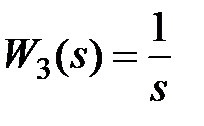

Рис.1. Структурная схема САУ

Для решения указанных задач запускаем MatLab кликом правой кнопки (ПК) мыши по соответствующему ярлыку.

1. Создаем m-файл, для чего в левом верхнем окне инструментальной панели пакета MATLAB нажимаем File, New или нажимаем окно .

2. В открывшемся окне Editor создаем файл, позволяющий получить следующие передаточные функции:

- передаточную функцию разомкнутой системы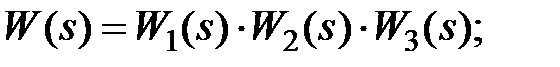

- передаточную функцию по ошибке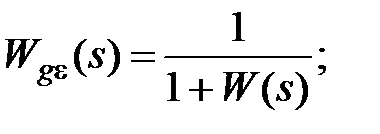

- передаточную функцию замкнутой системы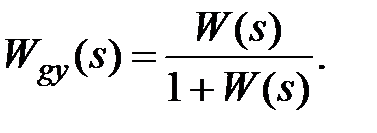

С указанной целью записываем следующую программу и обязательно сохраняем её любым именем на английском языке:

1. %ВАРИАНТ №___(если строка содержит знак %, вся информация,

% следующая за ним программой игнорируется)

2. W1=tf(20*[1 1],[1 0]) % в квадратных скобках записываются коэффициенты числителя и знаменателя, начиная со старшей степени s

3. W2=tf([1 1],[10 1])

4. W3=tf(1,[1 0])

% Для проверки правильности набора в конце строк 2,3,4 не ставим ";". % При этом будет распечатка введенных функций.

% Если ошибок нет, продолжаем набирать программу.

5. W12=W1*W2

6. Wge=1/(1+W12*W3)!!!!

7. Wgy=feedback(W12*W3,tf(1,1))

Результат работы программы (выделен жирным шрифтом) при построчном введении команд (цифры в начале каждой строки не вносятся) имеет следующий вид:

>> W1=tf(20*[1 1],[1 0])

Transfer function:

20 s + 20

---------

s

>> W2=tf([1 1],[10 1])

Transfer function:

s + 1

--------

10 s + 1

>> W3=tf(1,[1 0])

Transfer function:

-

s

>> W12=W1*W2

Transfer function:

20 s^2 + 40 s + 20

------------------

10 s^2 + s

>> W=W12*W3

Transfer function:

20 s^2 + 40 s + 20

------------------ % W – перед. Ф-я РАЗОМКНУТОЙ СИСТЕМЫ

10 s^3 + s^2

>> Wge= feedback(1/ W,tf(1,1))

Transfer function:

10 s^3 + s^2

---------------------------

10 s^3 + 21 s^2 + 40 s + 20

>> Wgy= feedback(W,tf(1,1))

Transfer function:

20 s^2 + 40 s + 20

---------------------------

10 s^3 + 21 s^2 + 40 s + 20

В передаточных функциях Wge и Wgy использованы выражения feedback и tf(1,1), которые подразумевают использование в САУ главной единичной обратной связи.

При запуске записанной в Editor программы нажатием ПК на её инструментальной панели окна (показано стрелкой)

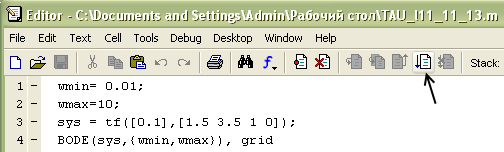
результат будет аналогичным, но все передаточные функции будут распечатаны в поле Command Window подряд:

>> W1=tf(20*[1 1],[1 0])

W2=tf([1 1],[10 1])

W3=tf(1,[1 0])

Transfer function:

20 s + 20

--------- % W1

s

Transfer function:

s + 1

-------- % W2

10 s + 1

Transfer function:

- % W3

s

>> W12=W1*W2

Transfer function:

20 s^2 + 40 s + 20

------------------

10 s^2 + s

>> W=W12*W3

Transfer function:

20 s^2 + 40 s + 20

------------------ % W – перед. Ф-я РАЗОМКНУТОЙ СИСТЕМЫ

10 s^3 + s^2

>> Wge= feedback(1/ W,tf(1,1))

Transfer function:

10 s^3 + s^2

--------------------------- % передаточная функция по ошибке Wge

10 s^3 + 21 s^2 + 40 s + 20

>> Wgy=feedback(W,tf(1,1))

Transfer function:

20 s^2 + 40 s + 20

--------------------------- % передаточная функция замкнутой системы Wgy

10 s^3 + 21 s^2 + 40 s + 20

Примечание. Можно было бы сразу записать требуемые передаточные функции, самостоятельно раскрыв полиномы числителя и знаменателя (1), но, как показано выше, это за нас легко делает MATLAB.

Итак, предварительный этап завершён. Приступим к выполнению пунктов задания.

1. Функцией BODE оценить устойчивость и, если система устойчива, – запасы устойчивости по фазе и по модулю. Эта функция предназначена для исследования частотных свойств заданной системы по её передаточной функции в разомкнутом состоянии W(s). Задаем команду

Bode (W), grid on % и получаем график (рис. 2)

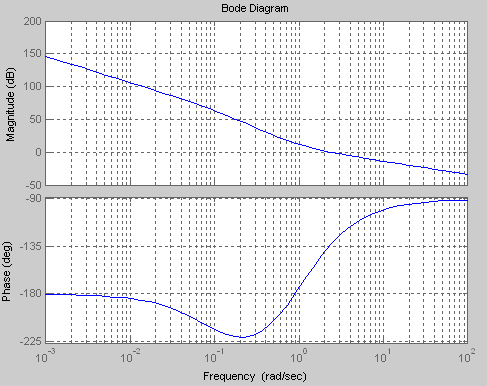
Рис. 2. Частотные характеристики заданной системы

Верхний график показывает, как изменяется модуль комплексного коэффициента передачи (ККП) разомкнутой системы при изменении частоты. При этом модуль оценивается в децибелах, т.е. по оси ординат откладывается Magnitude=20lg(A (ω)),

где 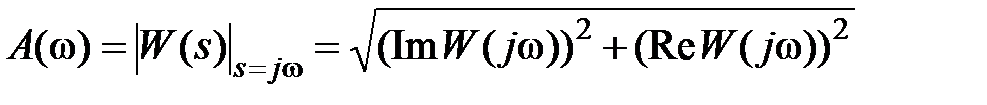. (2)

Нижний – дает представление об изменении фазовой характеристики ККП разомкнутой системы

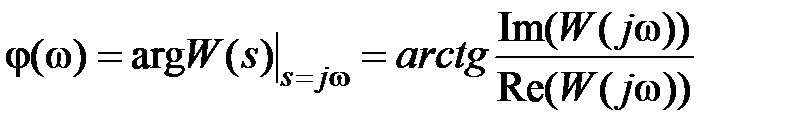(3)

в том же диапазоне частот. Можно изменить диапазон частот, указав его как {ωmin,ωmax}. Например, для рассматриваемой САУ функция

Bode (W,{0.03,1000}), grid on % дает рис. 3

На этом рисунке нанесены две частоты:

- ω_ср – частота, на которой модуль (2) равен 1. Она называется частотой среза, т.к. до неё, т.е. при изменении 0≤ω<ω_ср модуль больше 1, при ω_ср<ω≤∞ модуль меньше 1 (соответственно lg(A (ω)) отрицательный, что видно из графиков рис. 2, 3):

- ω_кр – частота, при которой фаза (3) равна -180^о. Она называется частотой критической.

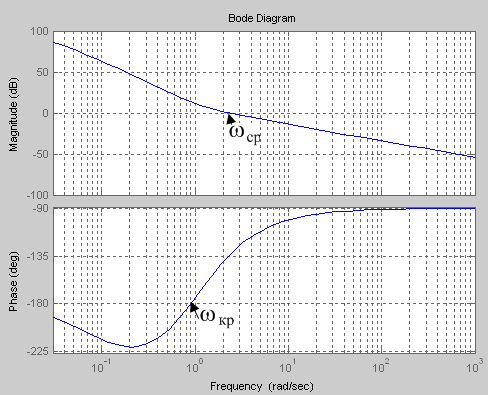
Рис. 3, а. Частотные характеристики с указанием частот ω_ср и ω_кр

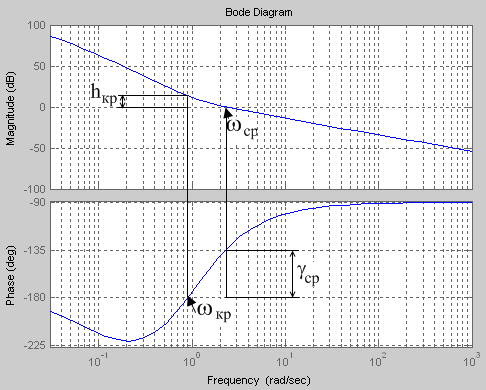
Рис. 3, б. Частотные характеристики с указанием запасов устойчивости

Соотношение указанных частот определяет устойчивость системы:

а) ω_ср<ω_кр – система не устойчива;

б) ω_ср=ω_кр ­ – система на границе устойчивости;

в) ω_ср>ω_кр – система устойчива, можно определить запасы по фазе и по модулю.

Из рис. 3, б видно: частота среза ω_ср=2.3 рад/с, частота критическая ω_кр=0.9 рад/с. Следовательно, рассматриваемая система устойчива. Запас устойчивости по фазе определяется как фаза на частоте среза ω_ср. В частности,

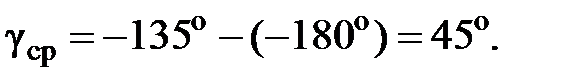Запас устойчивости по модулю – как величина модуля в дБ на частоте ω_кр, он составляет согласно рис. 3, б примерно 15 дБ.

Дата добавления: 2015-05-09