Модель энергетически рациональной структуры движения 3 страница

где wб - угловая скорость вращения бедра относительно туловища;
lб - расстояние от тазобедренного до коленного сустава (длина бедра), то есть радиус вращения коленного сустава относительно тазобедренного.

Если угол между Vотн и Vпер равенb, то строя параллелограмм скоростей, можем рассчитать модуль (величину) абсолютной скорости по формуле:

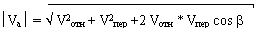
Скорость тазобедренного сустава Vтб и угловую скорость вращения бедра относительно туловища wсб рассчитывают по промеру движения. Графическое определение абсолютной скорости коленного сустава позволяет выявить составляющие, из которых она складывается, а следователь-но, направленно влиять на параметры движения, формирующие эту скорость.
На рис. 4.3 показано графическое определение скорости голеностопного сустава в цикле бегового шага.
Для анализа и корректировки спортивной техники необходим набор биохимических характеристик, изучение взаимосвязи которых позволяет тренеру получить объективные данные о структуре движения спортсмена.
В процессе анализа и оценки техники движения изучение его кинематики имеет самостоятельное и очень важное значение. Это вызвано тем, что кинематические показатели техники, как наиболее изученные, часто являются предметом сложившихся представлений о технике того или иного движения, которые можно рассматривать в качестве критериев технического мастерства.

Измерение и воздействие непосредственно на динамические характеристики движения на практике весьма затруднительно. В то же время изучение кинематических характеристик (в виду относительной простоты их регистрации и расчетов), управление которыми позволяет изменять динамику движения, является весьма перспективным направлением в изучении и совершенствовании техники движений.
Судить о рациональной технике бега можно только на основе знаний его кинематической структуры, то есть наиболее устойчивых закономерностей связей отдельных элементов в системе движений бегуна (линейных и угловых перемещений, скоростей и ускорений отдельных звеньев и суставов). Перемещения, скорости, ускорения - это структурные элементы системы движений.

5. ДИНАМИКА ДВИГАТЕЛЬНЫХ ДЕЙСТВИЙ
5.1. Две задачи динамики в анализе техники двигательных действий
Раздел механики, который изучает зависимость между механическим движением и действующими силами, называется динамикой. В механике под силой понимают меру механического взаимодействия тел.
Сила не является причиной движения (может быть движение без действия сил - движение по инерции). Сила - это причина изменения движения. А изменение движения проявляется в изменении скорости. Мерой же изменения скорости является ускорение.
Основной закон динамики связывает силу (причину изменения движения) с ускорением (мерой изменения движения).

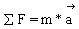
Разрешение этого закона лежит в основе решения всех задач динамики. Всякая задача состоит в решении, нахождении каких-то величин. Одни величины заданы, другие - надо найти. Какие величины заданы, а какие надо найти должен знать тренер в зависимости от задач исследования.
При анализе техники спортивных исследований современный тренер сталкивается с задачей двоякого рода, прямой и обратной.
Первая (прямая) задача динамики решается в том случае, когда известно движение тела, его частей или спортивных снарядов, то есть известны траектории, скорости, ускорения (эти кинематические характеристики могут получаться путем, например, кинорегистрации движения). При этом решается вопрос о том, под действием каких сил происходит это движение.
На языке педагогики - при решении первой задачи динамики - зада-на техника движения (закон движения), то есть задано движение то, какое оно есть, как его выполняет конкретный исполнитель, а мы определяем, при каких силах эта техника выполнима. Решение этой задачи позволяет подобрать тесты, упражнения для обучения этому движению. Решение первой задачи широко распространено в протезировании.
Вторая (обратная) задача динамики решается в том случае, когда известны силы, действующие на тело человека, отдельные его звенья или на спортивные снаряды. При этом решается вопрос о том, каким будет движение под действием от этих сил. Например, если известно, какая сила действовала на ядро при финальном усилии атлета, то можно определить, как высоко и далеко улетит ядро, сколько времени оно будет в полете и т.д.
Первая задача механики в практике исследования техники спортивных движений решается намного чаще, чем вторая. Однако вторая (основная) задача механики имеет большее практическое значение и в общем случае является более сложной, чем первая.
Вторая задача динамики позволяет, используя средства аналитической механики и исходя из общих законов движения, моделировать двигательные действия, то есть находить оптимальные варианты спортивной техники. Первая задача же в своем решении ограничивается регистрацией характеристик лишь данного, конкретного способа выполнения движения.
Понимание вопросов, которые могут быть определены при решении двух задач динамики, способствуют формированию педагогического мышления.
5.2. Динамические характеристики
Динамические характеристики делятся на: 1) характеристики, отражающие меру взаимодействия тел и служащие для объяснения взаимодействия тел. Они характеризуют сам процесс взаимодействия; 2) Характеристики, отражающие изменение состояния тел в результате взаимодействия и служащие для объяснения изменения состояния тел. Они характеризуют результат взаимодействия тел.

I. Характеристики, отражающие меру взаимодействия тел:
1) сила F, момент силы М (F) - меры механического взаимодействия тел. В результате действия силы или момента силы - изменяется скорость, то есть изменяется движение. Мерой изменения скорости является ускорение.
Основной закон динамики для поступательного движения выражается формулой: 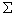F = m * a. Ускорение, которое получает тело под действием силы, зависит от его массы. Сравнивая действие одной и той же силы на разные тела, приходим кандидат понятию об инертности. Инертность - это свойство тел быстрее или медленнее изменять скорость своего движения под действием приложенных сил. Это свойство зависит от количества заключенного в теле вещества (материи). Величина, зависящая от количества вещества данного тела и определяющая меру его инертности (сопротивления) при поступательном движении называется массой. Тело с большой массой трудно сдвинуть, а в если сдвинули - трудно остановить.
В случае вращательного движения мало знать массу тела, важно еще распределение массы относительно оси вращения. Например, фигурист при вращении прижимает руки к туловищу, а затем поднимает их в стороны. Общая масса системы при этом не изменяется, а распределение масс становится другим, и это сказывается на движении (оно замедлится).
В механике вводится характеристика, определяющая меру инертности (сопротивления) тела во вращательном движении, зависящая от распределения массы относительно оси вращения, момент инерции тела. Момент инерции тела - это скалярная величина, равная произведению движущейся массы на квадрат ее расстояния от оси вращения: 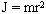, где r - радиус инерции, характеризующий распределение масс относительно оси вращения.

II. Характеристики, отражающие изменение состояния тел в результате взаимодействия:

1. Количество движения - это векторная величина, равная произведению массы точки на вектор ее скорости и направления, как и скорость точки, по касательной кандидат траектории движения:

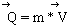
Количество движения является мерой поступательного движения, характеризующего его способность передаваться от одного тела кандидат другому в виде механического движения. Можно сказать, что количество движения тела - это мера его способности двигаться в течение некоторого времени против действия тормозящей силы. В результате взаимодействия нашего тела с опорой изменяется количество движения нашего тел. Чем больше количество движения (большую скорость) мы приобрели в результате взаимодействия с опорой, тем больше мы двигается против действия силы тяжести, то есть тем выше будет прыжок.
2. Кинематический момент. Мерой изменения состояния тела во вращательном движении является момент количества движения (кинематический момент):

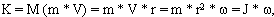
где К - кинетический момент,
J - момент инерции,
- угловая скорость.

3. Кинетическая энергия. Энергия тела - это его способность совершать работу. Кинетическая энергия тела при поступательном движении равна половине произведения массы тела на квадрат его скорости:

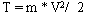
Во вращательном движении:

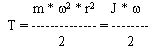
Кинетической энергией тела называется энергия, зависящая от механического движения тела. Она измеряется той работой, которую тело может совершить при его затормаживании.
Количество движения и кинетический момент отражают изменение состояния в результате действия силы во времени. Кинематическая энергия отражает изменение состояния в результате действия силы на участке перемещения.
Если скорость и ускорение являются кинематическими мерами изменения движения, то количество движения, кинетический момент и кинетическая энергия являются динамическими мерами изменения движения. Сведем рассмотренные характеристики в табл.2.

5.3. Теоремы динамики и законы сохранения применительно к анализу спортивных движений
Теоремы динамики связывают характеристики, отражающие меру взаимодействия тел, с характеристиками, отражающими изменение со-стояния тел. Эти теоремы позволяют решить некоторые практические частные задачи, а закон сохранения позволяет объяснить некоторые явления.
Изменяющимися и сохраняющимися величинами являются V; mV; 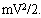. Сохраняются эти величины, если нет взаимодействия. Механика изучает условия, при которых происходят изменения этих величин или эти величины сохраняются (не изменяются).
1. Теорема о движении центра масс. Центр масс движется как материальная точка, масса которой равна массе всей системы, кандидат которой приложены все внешние силы, действующие на систему:

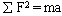
Если тело движется поступательно, то его движение полностью определяется движением его центра масс (поступательно движущееся тело можно всегда рассматривать как материальную точку, масса которой равна массе тела).
Закон сохранения движения центра масс. Если сумма всех внешних сил, действующих на систему, равна нулю, то центр масс этой системы движется с постоянной по модулю и направлению скоростью, то есть равномерно и прямолинейно: иными словами, если в начале центр масс был в покое, то он и останется в покое. Действие внутренних сил движения центра масс изменить не может.
Движение по горизонтальной плоскости. При отсутствии трения человек с помощью своих мускульных усилий (силы внутренние) не мог бы двигаться вдоль горизонтальной плоскости, так как в этом случае -сумма проекций на горизонтальную ось ОХ всех приложенных кандидат человеку внешних сил (сила тяжести и реакции опоры) будет равна нулю, и центр масс человека вдоль горизонтальной плоскости перемещаться не будет. Если человек вынесет правую ногу вперед, то левая нога скользнет назад, а центр масс останется на месте.
При наличии же трения скольжению левой ноги будет препятствовать сила трения, которая в этом случае будет направлена вперед. Эта сила будет той внешней силой, которая позволяет человеку перемещаться в сторону ее действия (вперед).
2. Теорема об изменении количества движения. Изменение количества движений системы за некоторый промежуток времени равно импульсу всех внешних сил, действующих на систему. Внутренние силы изменить количество движения не могут. Математическое выражение этой теоремы: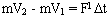
Если тело массы m двигалось со скоростью V1, то для того, чтобы оно стало двигаться со скоростью V2, надо приложить внешнюю силу F, которая бы за время Dt произвела это изменение движения. За счет внутренних сил (мышечных тяг) изменить количество движения, а следовательно, скорость центра масс и его траекторию не можем (можем изменить траекторию и траектории центров масс отдельных звеньев).
Закон сохранения количества движений. Если сумма всех внешних сил, действующих на систему, равна нулю, то количество движения системы не изменяется (сохраняется). Если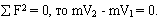
Пример. В гребле весло сообщает некоторой массе воды движение, отбрасывая эту массу воды назад. Если рассматривать эту массу воды и лодку (с веслом) как одну систему, то силы взаимодействия весла и воды как внутренние силы не могут изменить суммарное количество движения всей системы. Поэтому при отбрасывании массы воды назад, лодка полу-чает соответствующую скорость движения вперед, такую, чтобы общее количество движения системы не изменилось.
3. Теорема об изменении момента количества движения системы. Изменение момента количества движения системы равно импульсу момента всех внешних сил, действующих на систему.
Математическое выражение этой теоремы:

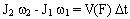
Если начальный момент количества движения тела был равен 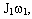, то для того, чтобы он изменился до величины 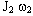надо, чтобы на тело в течение времени 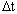действовал момент внешних сил M(F).
Закон сохранения кинетического момента. Если моменты внешних сил, действующих на тело, равны нулю, то кинетический момент не изменяется (сохраняется). Если M(F) = 0, то = 0. Внутренние силы изменить кинетический момент не могут.
Хорошо демонстрирует закон сохранения кинетического момента "платформа Жуковского" - это круглая платформа, которая с малым трением вращается вокруг вертикальной оси. На человека, стоящего на плат-форме, действуют две внешние силы - сила тяжести и сила реакции опоры. Момент этих сил относительно продольной (вертикальной) оси равен нулю, так как эти силы направлены вдоль этой оси. Если человек, разведя руки в стороны, толчком сообщит платформе вращение вокруг вертикальной оси, а своему телу кинетический момент 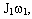, то величина 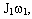в процессе вращения изменяться не будет (так как момент внешних сил равен нулю). Если, вращаясь, человек спустит руки вниз, то этим он уменьшит момент инерции тела. Произведение момента инерции на угловую скорость должно остаться постоянным, поэтому уменьшение момента инерции до величины 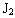сразу же вызовет увеличение угловой скорости до величины :

Во сколько раз 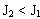, во столько же раз 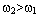. Этим приемом увеличения угловой скорости вращения пользуются в акробатике, фигурном катании, прыжках в воду и т.д.
Человек стоящий на платформе неподвижно , может за счет своих внутренних сил (мышечных усилий) повернуться в любую сторону, вращая вытянутую горизонтальную руку в любую сторону, вращая вытянутую горизонтальную руку в противоположном направлении. Угловая скорость вращения человека будет такой, чтобы в сумме величина кинетического момента системы осталось равна нулю. Этим способом также широко пользуются гимнасты, акробаты, прыгуны в воду и т.п. для создания вращения в безопорной фазе полета.
Раскачивание качелей. Силой давления ног (силы внутренние для системы человек - качели) качели раскачивать нельзя. Когда качели находятся в левом верхнем положении Ао, человек приседает. При прохождении качелей через вертикаль человек быстро выпрямляется. При этом массы тела приближаются к оси вращения, и момент инерции - уменьшается, а угловая скорость скачком возрастает. Это увеличение угловой скорости приводит к тому, что в правом верхнем положении качели поднимутся выше начального уровня Ао. В правом верхнем положении, когда 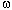= 0, человек приседает опять (на величине 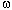это не скажется), а при прохождении через вертикаль - вновь выпрямляется и т.д.
Следует понимать, что теоремы динамики применяются для решения конкретных задач, связанных с определением механических характеристик. Законы сохранения движения чаще всего применяют для объяснения тех или иных явлений (можно ли совершить движение в тех или иных условиях, почему изменяется скорость при тех или иных условиях).
Какие же теоремы, в каких условиях применяются для решения задач? При изучении поступательного движения применяют теорему об изменении количества движения. При изучении вращательного движения применяют теорему об изменении кинетического момента.
5.4. Управление вращательным движением.
Управление вращательными движениями может быть понятно и объяснено на основании теоремы об изменении кинетического момента и закона сохранения кинетического момента.
Изменение кинетического момента равно импульсу момента внешних сил за заданный отрезок времени:

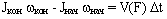
Если момент внешних сил V(F) равен нулю, то кинетический момент не изменяется (сохраняется):

I. Управление движением с изменением кинетического момента. При этом момент внешних сил не должен быть равен нулю 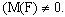Пример: человек стоит на платформе Жуковского. Отталкиваясь от пола, он сообщает вращение своему телу вокруг вертикальной оси. Чем сильнее будет отталкивание (чем больше 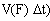, тем быстрее человек будет вращаться. В этом случае управление вращением сходно с управлением поступательным движением (чем больше импульс силы отталкивания 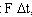тем больше приобретаемое количество движения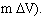
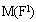II. Управление вращением с сохранением кинетического момента. Если момент внешних сил M(F) равен нулю, то кинетический момент есть величина постоянная = constanta. Если = 0, то изменить движение центра масс нельзя, но можно изменить угловую скорость вращения тела. Пример: фигурист вращается на льду вокруг вертикальной оси с угловой скоростью 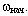Кинетический момент фигуриста равен 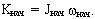Во время вращения на фигуриста действуют две внешние силы - сила тяжести - s и сила реакции опоры R (рис.5.3а). Моменты этих сил относительно оси вращения равны нулю (так как силы направлены вдоль оси вращения). Следовательно во время вращения кинетический момент фигуриста будет оставаться постоянным 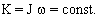Чтобы замедлить вращение, фигурист принимает положение "руки в стороны". Этим он увеличивает свой момент инерции Как только момент инерции увеличится, то сразу же уменьшится угловая скорость вращения так как кинетический момент, то есть произведение 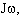должно остаться постоянным:


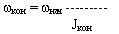
Во сколько раз 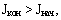во столько же раз и наоборот.
На основании этой же закономерности происходит управление скоростью вращения в безопорном положении. Пример: прыгун в воду вращается в положении "прогнувшись" с угловой скоростью. Вращение в полетной фазе происходит относительно фронтальной оси, проходящей через ОЦТ прыгуна (ось вращения направлена перпендикулярно плоскости чертежа). В полетной фазе на прыгуна действует одна внешняя сила - сила тяжести s (сопротивлением воздуха пренебрегаем). Момент силы тяжести относительно оси вращения равен нулю (так как сила тяжести пересекает ось вращения). Следовательно, в полетной фазе кинетический момент прыгуна будет величиной постоянной 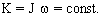Если примет положение "группировки", то его момент инерции уменьшится 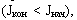а угловая скорость вращения увеличится 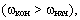так как кинетический момент прыгуна должен остаться постоянным: 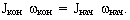Во сколько раз уменьшится 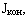во столько же раз увеличится 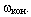Эту закономерность изменения скорости вращения в безопорной фазе использует гимнасты и акробаты.
В приведенных выше примерах изменение скорости вращения происходило при условии, что 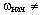0, то есть задавалось (как правило, при отталкивании от опоры) начальное вращение (начальный кинетический момент).
Рассмотрим случай, когда начальный кинетический момент равняется нулю, то есть 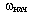= 0. Пример - падение кошки с высоты без начального вращения. В этом случае: 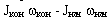= 0; так как 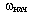= 0, то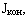 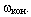= 0; 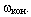= 0. Иными словами, если нет начального момента вращения 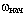, то и конечное вращение будет равно нулю. Но эти рассуждения справедливы лишь для твердого, неизменяемого тела. Из практики известно, что кошка, падающая спиной вниз, в полете успевает повернуться и приземляется всегда на лапы. Как это происходит? Тело кошки состоит из подвижных звеньев, которые вращаются друг относительно друга. Кинетический момент туловища кошки равен 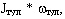, кинетический момент хвоста кошки равен 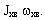. При этом суммарный кинетический момент тела кошки остается равным нулю:

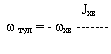
Знак "минус" показывает, что вращение туловища и хвоста кошки происходит в разных направлениях. При этом во сколько раз туловище кошки массивнее ее хвоста во столько раз кошка должна вращать свой хвост, чтобы успеть повернуть туловище лапами к земле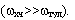
Эту закономерность используют гимнасты для создания вращения в безопорной фазе: скручивание туловища и рук в сторону вызывает поворот ног гимнаста в другую сторону:

Основы биомеханического анализа

1. ЭЛЕМЕНТЫ БИОМЕХАНИКИ
Биомеханика - учение о двигательной деятельности живых существ. Спортивная биомеханика - раздел биомеханики, изучающий двигательную деятельность спортсменов и людей, занимающихся массовыми формами физической культуры.
Основные задачи биомеханики:
1) раскрыть закономерности двигательной деятельности;
2) найти пути ее совершенствования.
Современная биомеханика - методически хорошо оснащенная, быстро прогрессирующая отрасль знаний. Она пополняется новыми разделами. Уже сформировались:

- частная биомеханика, посвященная биомеханическим закономерностям отдельных видов движений (например, биомеханика борьбы, биомеханика плавания и т.п.);
- дифференциальная биомеханика, изучающая индивидуальные и групповые (возрастные, квалификационные и т.д.) особенности моторики.
Совсем недавно возникли и интенсивно развиваются: инженерная биомеханика, основные достижения которой связаны с созданием роботов; медицинская биомеханика, исследующая причины, последствия и способы профилактики травматизма, прочность опорно - двигательного аппарата, вопросы протезирования; эргонометрическая биомеханика, изучающая взаимодействие человека с окружающими предметами с целью их оптимизации.
Для биомеханики характерна педагогическая направленность. По существу она служит связующим звеном между достаточно сложными теоретическими дисциплинами, объясняющими закономерности двигательной деятельности, и спортивно прикладными дисциплинами. Опираясь на знание основ биомеханики, педагогу легче оптимизировать двигательную деятельность своих учеников. Но, чтобы решить эту задачу, необходимо уметь анализировать двигательную деятельность ("читать движения"). Процедура биомеханического анализа техники движений включается в себя: определение топографии работающих мышц, анализ кинематики, динамики и энергетики, а также выявление оптимальных двигательных режимов. Когда анализируется тактика двигательной деятельности, необходимо, кроме того, установить, из каких двигательных действий она состоит.
2. ОСНОВЫ БИОМЕХАНИЧЕСКОГО КОНТРОЛЯ
Овладение культурой движений и повышение технико-тактического мастерства невозможно без биомеханического контроля. Двигательную культуру определяют:
- объем техники и тактики (перечень технических приемов и тактических вариантов, которыми владеет человек); например, в объем техники теннисиста входит удар справа, удар слева, различные виды подач и т.д.);
- разносторонность техники и тактики (степень разнообразия технических приемов и тактических вариантов, используемых человеком); например, биатлонист должен владеть современной техникой и тактикой в гонке, при подходе к огневому рубежу и на огневом рубеже.

Примечание: различают общий и соревновательных объем, а также общую и соревновательную разносторонность техники и тактики, поскольку в стрессовой ситуации использует только ту часть своего технико-тактического арсенала, которая наиболее освоена.
- освоенность техники и тактики (их стабильность в стандартных условиях и устойчивость в усложненных условиях, при перерывах в тренировке и т.п.); например, сохранились кинокадры бега В.Веденина, где этот великолепный мастер до последних метров дистанции сохраняет филигранную технику лыжного хода, а сразу после финиша падает на руки своих товарищей из-за крайнего утомления;
рациональность техники и тактики (степень соответствия используемых технических приемов и тактических вариантов целям двигательной деятельности и условиям, в которых она протекает); Например, из традиционных способов передвижения на лыжах на равнинной лыжне при хорошем скольжении рационален одновременных одношажный или бесшажный ход, а при преодолении крутого подъема - ступающий. Другой пример: при стремлении к экономичности рациональна тактика постоянной скорости, а при стремлении к наивысшему результату (на спринтерских и средних дистанциях) - тактический вариант - "вовсю".
Таким образом, рациональность характеризует способ двигательной деятельности безотносительно к личности исполнителя. При определении рациональности того или иного двигательного режима ориентируются на средние физические возможности людей разного пола, возраста, квалификации и т.п.;
- эффективности техники и тактики (степень соответствия используемых технических приемов и тактических вариантов двигательной деятельности и индивидуальным возможностям человека). Эффективной называется оптимальная техника или тактика, т.е. наилучшая для данного конкретного человека - в отличие от рациональной, которая является наилучшей для "среднего" человека.
Для количественной оценки показателей рациональности и эффективности применяются различные показатели, в зависимости от основного критерия оптимальности:

Дата добавления: 2015-05-09