
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Исходные данные. I. Итерационный метод нахождения корня уравнения F(a, y) = 0:
|
|
|
|
I. Итерационный метод нахождения корня уравнения F (a, y) = 0:
а) Метод касательных. При заданном начальном приближении корня y(0) по формуле
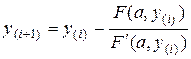
находятся очередные приближения до тех пор, пока не окажется

Тогда y ( k ) = y * принимается за искомое значение корня.
Формальными параметрами процедуры нахождения корня должны быть: начальное приближение корня y(0), точность приближения e, функции F (x, y), F¢ (x, y) и значение параметра x.
б) Метод половинного деления отрезка. При заданных начальных границах интервала  и
и 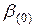 , содержащего искомый корень, итерационным процессом вычисляются новые границы
, содержащего искомый корень, итерационным процессом вычисляются новые границы 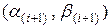 по границам
по границам 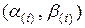 :
:
- вычисляется 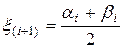 ;
;
- если  , то искомый корень
, то искомый корень  ;
;
- если 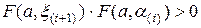 , то
, то 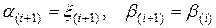 ;
;
- если  , то
, то 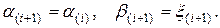
Итерации проводятся до тех пор, пока на некотором шаге не окажется  ; тогда
; тогда  принимается за искомое значение y *.
принимается за искомое значение y *.
Формальными параметрами процедуры нахождения корня должны быть: начальные границы  ,
, 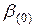 , точность приближения e, функция F (x, y) и значение ее параметра x.
, точность приближения e, функция F (x, y) и значение ее параметра x. 
в) Метод хорд. Этот метод отличается от предыдущего только тем, что точка  определяется другим выражением
определяется другим выражением
 .
.
II. Исходную функцию F (x, y) зададим в виде:
F (x, y) = y × f (x) + g (x) + h (y).
В качестве начального приближения выбрать (для x = a)
 .
.
В качестве начальных границ выбрать (для x = a)
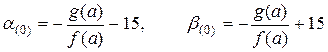 .
.
Функция F¢ (x, y) = f (x) + h ¢ (y)
Варианты задания функции g (x):
а)  ; г)
; г) 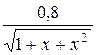 ;
;
б)  ; д)
; д) 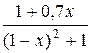 ;
;
в) 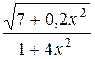 ; е)
; е)  .
.
Варианты задания функции f (x):
а) 3 + 2 x 2; г) 10,8 - x;
б) 6 + 9×½ x ½; д) 1,7 x 2 + 1;
в) 2× x 2 - x + 1,8; е) (1 + 0,6 x)2.
Варианты задания функции h (y) и h ¢ (y):
а) h (y) = -2,7 sin y; h ¢ (y) = -2,7 cos y;
б) h (y) = 1,14 cos2 y; h ¢ (y) = -1,14 sin 2 y;
в) h (y) = 0,2 e – y 2 ; h ¢ (y) = -0,4 ye - y 2;
г) h (y) = 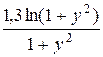 ; h ¢ (y) =
; h ¢ (y) = 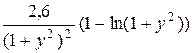 .
.
III. Числовые данные
| e | n | x 1 | x 2 | x 3 | x 4 | x 5 | x 6 | |
| а) | 0,1 | 1,1 | 1,5 | 1,8 | - | - | - | |
| б) | 0,2 | -0,8 | -0,2 | 1,4 | 1,9 | - | - | |
| в) | 0,1 | -0,6 | -0,1 | 1,7 | 2,2 | - | - | |
| г) | 0,3 | -4,1 | -2,1 | 1,6 | 2,4 | 2,5 | 3,0 | |
| д) | 0,2 | -2,7 | -1,8 | 1,1 | 2,1 | 2,6 | - | |
| е) | 0,3 | -1,8 | -1,2 | 1,5 | 1,9 | 2,3 | - |
1.3 Упорядочивание последовательности.
По заданным x 0 и n построить последовательность чисел 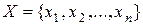 по закону
по закону 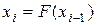 , i =1, 2, …, n. Затем эту последовательность упорядочить в новую последовательность
, i =1, 2, …, n. Затем эту последовательность упорядочить в новую последовательность  согласно правилу П и найти в Y номер r элемента, удовлетворяющего условию А.
согласно правилу П и найти в Y номер r элемента, удовлетворяющего условию А.
Входными данными программы являются значения x 0 и n; программа должна напечатать два массива чисел X и Y, также номер r. В программе предусмотреть:
- процедуру-функцию, вычисляющую значение F (x), с формальным параметром x;
- процедуру упорядочивания массива В размерности m в массив С в соответствии с правилом П - с формальными параметрами B, C, m.
Исходные данные
I. Функция F (x):
а) 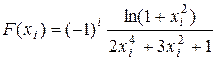 ;
;
б) 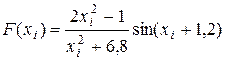 ;
;
в)  ;
;
г) 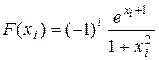 ;
;
д)  ;
;
II. Правило П упорядочивания массива X в массив Y:
а) 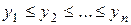 ;
;
б)  ;
;
в) 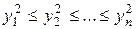 ;
;
г) 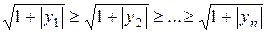 ;
;
д) любое отрицательное число левее любого положительного.
III. Условие А, которому должен удовлетворять элемент yr:
а) yr - первое слева положительное число (если таких чисел нет, то r = n + 1);
б) yr - первое справа отрицательное число (если таких чисел нет, то r = 0);
в)  ;
;
г) 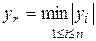 ;
;
д) 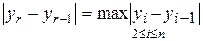 .
.
IV. Числовые данные
| а) | б) | в) | г) | д) | е) | |
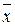
| 1,2 | 1,8 | -2,1 | -3,6 | 4,2 | -5,1 |
| n |
1.4 Оценка псевдослучайной последовательности. Образовать последовательность псевдослучайных чисел по рекуррентной формуле

при заданных x 0, x -1, x -2 и фиксированном значении a, i = 1, 2, …, N. Подсчитать x k - количество чисел этой последовательности, оказавшихся в полуинтервале
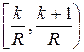 , k = 0, 1, …, R -1.
, k = 0, 1, …, R -1.
Вычислить математическое ожидание
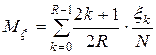
и дисперсию
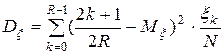 .
.
Провести вычисления для значения a = 0 и a = 1. Входными данными для программы служат значения x 0, x -1, x -2 , N, R; выходными данными - массив x [0, R -1], значения M x, D x для каждого значения a = 0 и a = 1.
В программе предусмотреть:
- процедуру-функцию, вычисляющую значение F (x, y, z, a), с формальными параметрами x, y, z, a;
- процедуру определения полуинтервала  которому принадлежит заданное число z, с прибавлением единицы к значению элемента массива x k - с формальными параметрами: числа R, Z и массив x[0, R -1].
которому принадлежит заданное число z, с прибавлением единицы к значению элемента массива x k - с формальными параметрами: числа R, Z и массив x[0, R -1].
Исходные данные
I. Функция F (x, y, z, a) = T (f (x, y, z, a)) причем функция f (x, y, z, a) определяется выражением:
а) | sin (ax + y - xz)|; е) 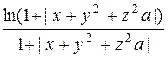 ;
;
б) 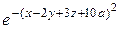 ; ж)
; ж)  ;
;
в) cos 2 (x + y - z - a); з) 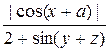 ;
;
г) 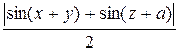 ; и)
; и) 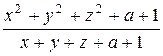 ;
;
д)  ; к)
; к)  .
.
II. Преобразование T (u) числа u задается следующим образом: если u = 0, u 1 u 2 u 3 … u 10 - представление в виде двоичной дроби с точностью до десятого знака после запятой (то есть 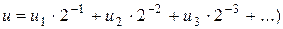 , то
, то
а) 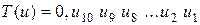 ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д)  ;
;
е) 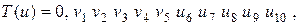 где
где
 ;
;
ж) 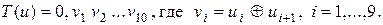
III. Числовые данные
| N | R | x 0 | x -1 | x -2 | |
| а) | 0,025 | 0,211 | 0,714 | ||
| б) | 0,230 | 0,050 | 0,928 | ||
| в) | 0,841 | 0,126 | 0,385 | ||
| г) | 0,052 | 0,568 | 0,687 | ||
| д) | 0,664 | 0,099 | 0,402 | ||
| е) | 0,273 | 0,591 | 0,741 |
1.5 Вычисление интеграла методом Монте-Карло.
Вычислить значения функции 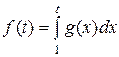 в заданных точках t 1, t 2, …, tm. Значение интеграла вычисляется приближенно по методу Монте-Карло: в интервале [1, t ] случайно выбираются M точек x 1, x 2, …, xM и
в заданных точках t 1, t 2, …, tm. Значение интеграла вычисляется приближенно по методу Монте-Карло: в интервале [1, t ] случайно выбираются M точек x 1, x 2, …, xM и 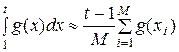 . Входными данными программы служат: числа m, M и массив значений ti, i = 1, 2, …, m.
. Входными данными программы служат: числа m, M и массив значений ti, i = 1, 2, …, m.
В программе предусмотреть:
- процедуру-функцию вычисления значения g (x), с формальным параметром x;
- процедуру без параметров образования «случайного» числа при i –ом обращении в процедуру из числа j i -1 образуется j i = F (j i -1) и затем xi = 1 + (t - 1) j i (значение j 0 =1).
Исходные данные
I. Подынтегральная функция g (x):
а) 2 x + 0,8; г) x + 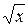 ;
;
б) x 2 - 1; д) x 3 + x - 1;
в) 1 + x + x 2; е) x 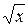 - 0,5.
- 0,5.
II. Рекуррента образования «случайного» числа
 , где функция h (z) задается выражением:
, где функция h (z) задается выражением:
а) | sin z |; г) 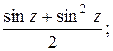
б) cos2 z; д) e - z ;
в)  е)
е) 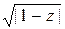 ,
,
и преобразование T - см. исходные данные предыдущей задачи.
III. Числовые данные
| M | m | t 1 | t 2 | t 3 | t 4 | |
| а) | 3,5 | - | - | |||
| б) | 6,5 | - | - | |||
| в) | 5,8 | 8,2 | 12,0 | - | ||
| г) | 4,3 | 6,0 | 10,2 | - | ||
| д) | 5,4 | 5,4 | 7,2 | 8,3 |
1.6 Вычисление вектора.
По заданному  , двум квадратным матрицам и функционалу F, заданному на векторах, вычислить вектор
, двум квадратным матрицам и функционалу F, заданному на векторах, вычислить вектор  по закону
по закону
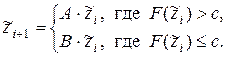
Входными данными программы служат: размерность n векторов, число С, а также элементы вектора 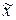 ; выходными данными - элементы вектора
; выходными данными - элементы вектора 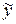 .
.
В программе предусмотреть:
- процедуру-функцию вычисления функционала F (a) с формальными параметрами: массив 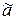 и его размерность m;
и его размерность m;
- процедуру умножения матрицы (квадратной) на вектор с формальными параметрами: массив D (матрица), массивы  и
и 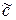 (векторы), размерность n (векторов матрицы).
(векторы), размерность n (векторов матрицы).
Примечание. Если элементы векторов и матриц - вещественные числа, то произведение матрицы D = (di, j) на вектор  = (b 1, …, bn) есть вектор
= (b 1, …, bn) есть вектор 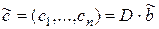 с компонентами
с компонентами
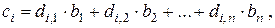
причем сложение и умножение - обычные операции. Если же элементы векторов и матриц - булевского типа, то в выражении для сi умножение понимается как конъюнкция, а сложение - как сложение по модулю 2.
Исходные данные
I. Функционал  для векторов с вещественными компонентами
для векторов с вещественными компонентами 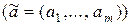
а) 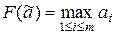 ; е)
; е)  ;
;
б)  ; ж)
; ж)  ; в)
; в) 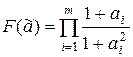 ; з)
; з)  ;
;
г) 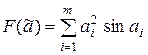 ; и)
; и) 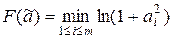 ;
;
д) 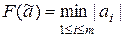 ; к)
; к)  .
.
II. Функционал  для векторов с булевскими компонентами
для векторов с булевскими компонентами
а)  = количество true в векторе
= количество true в векторе 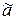 ;
;
б)  = количество true, предшествующих в
= количество true, предшествующих в 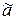 первому значению false (F (a) = m, если в
первому значению false (F (a) = m, если в 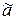 значений false нет);
значений false нет);
в) при трактовке true как 1 и false как 0 вектор 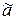 представляет в двоичной системе число
представляет в двоичной системе число  ;
;
г) 
д) 
е)  = максимальное количество значений true между двумя значениями false в векторе
= максимальное количество значений true между двумя значениями false в векторе 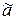 ;
;
ж) 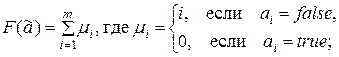
з) 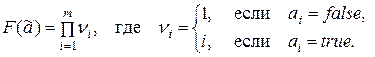
III. Числовые данные
Для элементов векторов и матриц - вещественных чисел
| а) | б) | в) | г) | д) | е) | |
| n | ||||||
| C | 0,5 | 5,8 | 1,2 | 9,6 | 4,3 | 8,6 |
Для элементов векторов и матриц - булевских чисел
| а) | б) | в) | г) | д) | е) | |
| n | ||||||
| C |
Элементы вектора 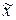 и матриц A, B выбираются произвольно.
и матриц A, B выбираются произвольно.
1.7 Вычисление матрицы.
Вычислить элементы квадратной матрицы М по выражению Â (A, B, X, Y), содержащему заданные матрицы A, B и числа x, y. Определить значение функционала F на матрице М. Входные данные для программы: число n - размерность матриц, числа x, y и элементы матриц A, B. Выходные данные: элементы матрицы М и значение функционала F (M).
В программе предусмотреть:
- процедуру-функцию вычисления функционала F (без параметров);
- процедуру для той операции над матрицами, которая входит в выражение Â.
Исходные данные
I. Выражение Â (A, B, X, Y) для вещественных матриц:
а) M = X × (A + y × B) + y × (B + x × A) (операция +)
б) 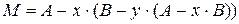 (операция -)
(операция -)
в)  (операция *)
(операция *)
г)  (операция /)
(операция /)
д)  (операция ´,
(операция ´,
причем A 2 = A ´ A, A 3 = A 2´ A).
Пояснение. Операции ×, +, - между числом и матрицей означает поэлементную операцию (между числом и каждым элементом матрицы); операции между матрицами +, -, *, / - операции поэлементные; операция ´ - обычное произведение матриц.
II. Функционал F
а)  ;
;
б)  ;
;
в)  - количество положительных чисел в i - й строке;
- количество положительных чисел в i - й строке;
г) F(M) = r, где r – номер того столбца, сумма элементов которого минимальна;
д) 
III. Числовые данные
| а) | б) | в) | г) | д) | е) | |
| x | 0,2 | 18,3 | 1,7 | 24,5 | 2,5 | 4,3 |
| y | 6,8 | 1,8 | 0,2 | 18,1 | 19,6 | 14,2 |
| n |
Элементы матриц А и В выбираются произвольно.
1.8 Преобразование матрицы.
По заданной матрице А (размерности n ´ n) вычислить новую матрицу X:
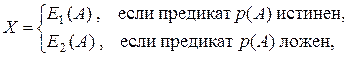
где Е 1 и Е 2 - заданные преобразования матрицы А. Входными данными программы являются: число n и элементы матрицы А; выходными - элементы матрицы X.
В программе предусмотреть:
- процедуру вычисления матрицы Е 1(А) с формальными параметрами: размерность матрицы m, массивы А и В (исходная матрица и вычисляемая);
- процедуру-функцию булевского типа вычисления значения предиката с формальными параметрами: размерность матрицы и массив ее элементов.
Исходные данные
I. Две различные операции Е 1 и Е 2 над вещественными матрицами из следующего списка:
а) транспонирование;
б) умножение на 3 всех элементов тех и только тех строк, в которых диагональный элемент больше 1;
в) возведение в l -ю степень (l = 3, 4);
г) замена элементов a i,j на sin a i,j для тех и только тех столбцов j, которые имеют в первой строке числа, принадлежащие интервалу [-1, +1] (т.е. -1 £ a i,j £ 1);
д) к элементам нечетных строк прибавить значение их логарифма;
е) преобразование в симметричную с сохранением элементов, находящихся справа от главной диагонали;
Операции Е 1 и Е 2 над булевскими матрицами:
ж) транспонирование;
з) инвертирование (замена true на false и false на true) элементов четных строк матрицы;
и) инвертирование элементов тех и только тех строк, которые на главной диагонали имеют true;
к) возведение в l -ю степень (l = 3, 4), при этом умножение трактуется как конъюнкция, а сложение – как неэквивалентность булевских чисел;
л) преобразование в симметричную с сохранением элементов, находящихся слева от главной диагонали;
м) в каждом нечетном столбце переставить местами первый и последний элементы, второй и предпоследний и так далее.
III. Предикат P (A) на вещественных матрицах:
а) все определители второго порядка положительны (т.е.
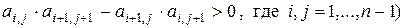 ;
;
б) каждая строка матрицы содержит и положительные и отрицательные числа;
в) в каждой строке и каждом столбце матрицы есть элемент по модулю не превосходящий 1;
г) для всех i и j таких, что i < j, имеет место a i , j < a j , i;
д)  ;
;
е) сумма элементов, находящихся слева от главной диагонали, вдвое превышает сумму элементов, находящихся справа от главной диагонали.
Предикат P (A) на булевских матрицах:
ж) все определители второго порядка равны true (определитель вычисляется по формуле
 ù
ù  , где i, j = 1, …, n -1);
, где i, j = 1, …, n -1);
з) каждая строка матрицы содержит значения как true, так и false;
и) в каждой строке количество значений true больше количества значений false;
к) в матрице имеется либо строка, либо столбец, целиком состоящий из true;
л) для всех i и j таких, что i < j, имеет место ai, j Ì a j , i;
м) количество значений true, находящихся слева от главной диагонали, больше количества значений false, находящихся справа от главной диагонали.
IV. Числовые данные. Размерность матрицы n = 5, 6, 7 или 8, а элементы матрицы выбираются произвольно.
1.9 Рекуррентное образование матрицы.
По двум заданным матрицам X и Y размерности n ´ m вычислить матрицу X 5 согласно следующему рекуррентному соотношению:
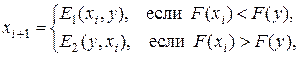
где x 0 = x, F (A) – функционал на матрице A, E 1 и E 2 – две операции над парой матриц образования новой матрицы.
Входными данными программы являются размерности n, m и элементы матриц X и Y; выходными данными – элементы матрицы X 5.
В программе предусмотреть:
- процедуру-функцию вычисления функционала F с формальными параметрами: размерности n и m массива и сам массив (элементов матрицы);
- процедуру образования матрицы согласно операции E 1 с формальными параметрами: размерности n, m и три массива (элементов матриц).
Исходные данные
I. Операции E 1 и E 2 выбираются из следующего списка (элементы матриц A, B и C = E (A, B) обозначены ai,j, bi,j, ci,j 1£ i £ n, 1£ j £ m.
В случае вещественных матриц:
а) 
б) 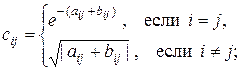
в) 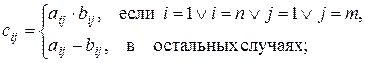
г) 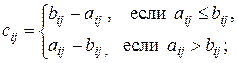
д) 
В случае булевских матриц:
е) 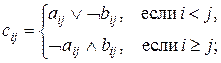
ж) 
з) 
и) 
к) 
II. Функционал F (A) на матрице A = (ai , j), 1 £ i £ n, 1 £ j £ m
В случае вещественных матриц:
а) 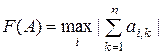 ;
;
б) 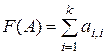 , где k = min(n, m);
, где k = min(n, m);
в)  ;
;
г)  , где j i - количество положительных чисел в i-ой строке матрицы A;
, где j i - количество положительных чисел в i-ой строке матрицы A;
д) 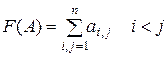 .
.
В случае булевских матриц:
е) 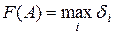 , где d i – количество true в i -й строке;
, где d i – количество true в i -й строке;
ж) F (A) количество false среди значений a 1,1, a 2,2 , …, ak, k, где k = min (n, m);
з) F (A) = max Li, где Li - целое число, двоичное представление которого дает i -ый столбец при замене true на 1 и false на 0;
и) общее количество true, среди значений ai,j, когда i < j;
к) F (A) = min(m i - n i), где m i - количество true и  n i - количество false в i -м столбце.
n i - количество false в i -м столбце.
III. Числовые данные
| а) | б) | в) | г) | д) | |
| n | |||||
| m |
Элементы матриц X и Y могут быть выбраны произвольно.
1.10 Определение характеристики степеней матрицы.
Для заданной квадратной матрицы A порядка m найти ее степени A 2, A 3, …, An и вычислить значения функционала F (Ai ), i = 1, …, n. Если для некоторого l (2 £ l £ n) окажется F (Al ) > c, то вывести на печать значение p = true и F (Al ), …, F (An); в противном случае напечатать значения p = false. Входными данными программы являются значения m, n, c и элементы матрицы A.
В программе предусмотреть:
- процедуру умножения двух матриц с формальными параметрами: три массива (элементов двух исходных матриц и матрицы их произведения) и порядок матрицы;
- процедуру-функцию вычисления значения функционала на матрице с формальными параметрами: массив элементов матрицы и ее порядок.
Исходные данные
I. Элементы матрицы A:
а) произвольные вещественные числа;
б) булевские числа;
в) вероятности, т.е. вещественные числа в пределах от 0 до 1 (стохастические матрицы).
II. Функционал F (A) на матрице – см. задачу 1.9.
III. Числовые данные
| а) | б) | в) | г) | д) | |
| n | |||||
| m | |||||
| с |
1.11 Преобразование сумм.
Функциональная сумма вида

задается массивом коэффициентов p 0, p 1, …, pr. По заданному выражению
F(p 1(x), p 2(x), p 3(x)) = Q (x)
над тремя такими суммами найти коэффициенты q 0, q 1, …, qr аналогичного вида суммы Q (x). Затем вычислить Q (xj), j = 1, …, m.
Входными данными программы являются: массивы коэффициентов сумм p 1(x), p 2(x), p 3(x); их размерность r; значения x 1, …, xm и число m. Выходными данными являются: массив коэффициентов q 0, q 1, …, qr и числа Q (x 1), …, Q (xm).
В программе предусмотреть:
- процедуры для тех операций над суммами, которые входят в выражение F с формальными параметрами: массивы (коэффициентов исходных сумм и результирующей) и их размерность;
- процедуру-функцию вычисления значения суммы p (x) в заданной точке с формальными параметрами: массив коэффициентов суммы и значение x.
Исходные данные
I. Задание функциональной суммы
а)  ;
;
б) 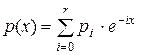 ;
;
в)  ;
;
г) 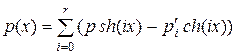 .
.
II. Выражение 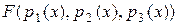 :
:

(операции – суммирование двух сумм, интегрирование одной суммы);

(операции – суммирование двух сумм и дифференцирование одной суммы);

(операции – вычитание одной сумм из другой и интегрирование одной функции);
г) 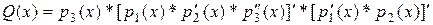
(операции – дифференцирование одной суммы и *);
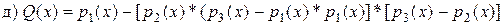
(операции – вычитание одной суммы из другой и *);
е) 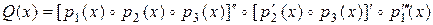
(операции – дифференцирование суммы и 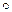 );
);

(операции – вычитания и 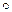 );
);
з) 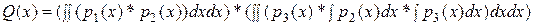
(операции – интегрирование и *).
Примечание. Если  и
и 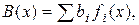 то сумма
то сумма  определяется так:
определяется так:

III. Числовые данные
| а) | б) | в) | г) | д) | |
| r | |||||
| m | |||||
| x 1 | -2,72 | -3,18 | -3,57 | -0,41 | -2,17 |
| x 2 | -0,04 | -1,92 | 0,82 | 1,63 | 4,31 |
| x 3 | 1,10 | 2,71 | 4,44 | 5,17 | |
| x 4 | 5,07 | 4,18 |
1.12 Арифметические операции над двоичными кодами.
Каждое целое число x (| x | £ 2 n –1) задается булевским массивом размерности n +1: массив (x0, x 1, …, xn) задает число
a 1× 2 n -1 + a 2× 2 n -2 + … + an -1× 2 + an,
где

причем знак числа определяется по x 0: знак +, если x 0 = true, и знак -, если x 0 = false.
По заданной функции F (x, y, z) и трем числам x, y, z (в виде булевских массивов) вычислить число u = F (x, y, z) - также в виде булевского массива. Полученное число вывести на печать. Входными данными программы являются: n и три булевских массива; выходным значением является u.
Функция F (x, y, z) содержит операции; для ее вычисления в программе предусмотреть процедуры выполнения этих операций над булевскими векторами.
Исходные данные
I. Функция F (x, y, z):
а)  ; (операции + и)
; (операции + и)
б) 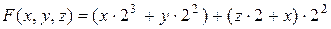 ; (+ и ×2 i)
; (+ и ×2 i)
в)  ; (+ и
; (+ и  i)
i)
г)  ; (- и
; (- и  )
)
д)  ; (- и
; (- и  i)
i)
е)  ; (+, ×2 i,
; (+, ×2 i,  i)
i)
ж)  ; (+, -,
; (+, -,  )
)
з)  ; (+,
; (+,  i,
i,  )
)
и) 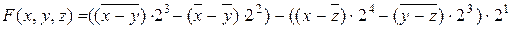 ;(-,
;(-,  ,×2 i)
,×2 i)
к) 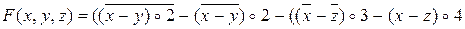 . (-,
. (-,  ,
,  i)
i)
Пояснение.
- операция + определяется как сложение чисел по модулю 2 n;
- операция - определяется как вычитание чисел по модулю 2 n;
- операция ×2 i – умножение числа на ×2 i (результат берется по модулю 2 n);
- операция  i - циклического сдвига значащих разрядов числа на i позиций вправо;
i - циклического сдвига значащих разрядов числа на i позиций вправо;
- операция  - изменения значащих разрядов числа на противоположное.
- изменения значащих разрядов числа на противоположное.
Старшими считаются операции ×2 i,  i,
i,  , младшими +, -.
, младшими +, -.
II. Вывод числа u - результата.
а) в виде массива булевских чисел;
б) в виде десятичного числа (перевод числа u в десятичную систему оформить в виде процедуры функции);
в) в шестнадцатеричном виде.
III. Числовые значения
| а) | б) | в) | г) | д) |
Значения булевских массивов для x, y, z произвольны.
|
|
|
|
|
Дата добавления: 2015-05-09; Просмотров: 474; Нарушение авторских прав?; Мы поможем в написании вашей работы!