Наблюдение и измерение цифровых изображений

Цифровое изображение хранится в памяти компьютера, в общем случае, в виде прямоугольной матрицы, элементы 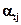которой несут информацию об оптических плотностях или цвете элементарных участков изображения, а номера i строки и j столбца элемента 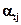определяют его положение в матрице. Нумерация строк и столбцов матрицы цифрового изображения начинается с нуля.

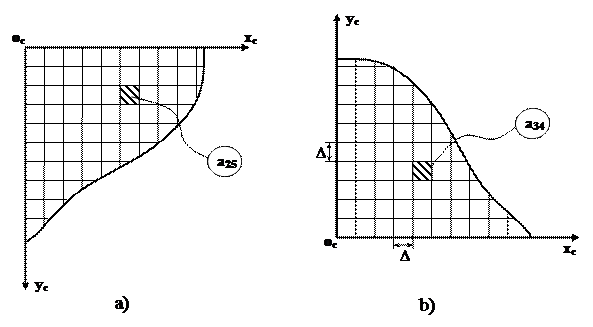
Рис.1.1

Координаты центров пикселей определяют в левой прямоугольной системе координат о_C x_C у_C (рис.1.1a), началом которой является левый верхний угол цифрового изображения и в правой - о_C x_C у_C (рис.1.1b), началом которой левый нижний угол цифрового изображения. В обеих системах координат ось x параллельна строкам, а ось y – столбцам матрицы цифрового изображения.

Левая система координат принята при записи изображений в файл во всех форматах и используется в большинстве программ по обработке изображений. В фотограмметрии традиционно применяется правая система координат снимка, и в большинстве современных цифровых фотограмметрических систем используют именно эту систему координат.

Пиксельные координаты (единицей измерения, в этом случае, является пиксель) центров пикселей в системе координат цифрового изображения о_C х_C у_C определяют по формулам:

. (1.1)

Для измерения координат точек цифрового изображения его визуализируют на экране дисплея. Если пиксель изображения на экране дисплея соответствует пикселю исходного цифрового изображения, то с помощью “мыши” или клавиатуры компьютера можно навести измерительную марку, формируемую в виде цифрового изображения на экране дисплея, на точку изображения с точностью до одного пикселя.

Для получения подпиксельной (субпиксельной) точности можно увеличить матрицу изображения на экране монитора относительно исходного цифрового изображения. В этом случае каждый пиксель исходного изображения будет изображаться матрицей n×n пикселей, численное значение всех элементов a'_ij которой будут равны численному значению элемента 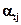матрицы исходного изображения.

Пиксельные координаты точек увеличенного изображения можно измерить с точностью до 1/n пикселя исходного изображения (рис.1.2.).

Рис. 1.2

Пиксельные координаты (в пикселях исходного изображения) элемента a'_ij увеличенного изображения определяют по формуле:

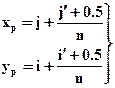, (1.2)

в которых: i,j - номера строки и столбца элемента матрицы исходного изображения, в котором находится элемент a'_ij увеличенного изображения:

i’,j’ - номера строки и столбца элемента a`_ij подматрицы n×n;

n – коэффициент увеличения изображения.

Например, для элемента a’₂₃ (рис.1.2) пиксельные координаты:

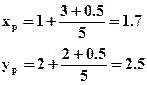
Значения физических координат центров пикселей цифрового изображения можно определить по значениям их пиксельных координат, если известны физические размеры стороны пикселя изображения Δ (предполагается, что пиксель имеет форму квадрата).

Значения физических координат определяют по формулам:

. (1.3)

Например, координаты центра пикселя, соответствующего элементу a’₂₃ (рис.1.2) при величине Δ=20 мкм будут равны х_c = 34 мкм и y_c = 50 мкм.

В некоторых цифровых системах начало системы координат цифрового изображения о_c х_c у_c выбирают в центре пикселя, расположенного в нижнем левом углу цифрового изображения (рис.1.3).

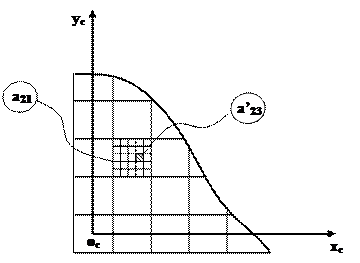
Рис.1.3

В этом случае значения пиксельных координат вычисляют по формулам:

, (1.4)

при измерениях с точностью до пикселя и по формулам:

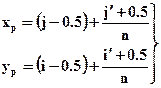, (1.5)

при измерениях с подпиксельной точностью.

Например, для того же элемента a’₂₃ (рис.1.3) пиксельные координаты равны:

Рассмотренный выше метод измерения цифрового изображения с подпиксельной точностью требует его увеличения на экране дисплея компьютера. Однако, даже при увеличении цифрового изображения только в два раза, на экране дисплея исходный аналоговый снимок изображается с весьма значительным оптическим увеличением. Так, например, снимок, преобразованный на сканере, с размером пикселя 14 мкм на экране дисплея с размером зерна 0.28 мм при увеличении цифрового изображения снимка в 2 раза имеет оптическое увеличение 40 раз. Такое увеличение приводит к значительному ухудшению изобразительных свойств наблюдаемого изображения и, как следствие, к снижению точности наведения измерительной марки на измеряемые объекты на изображении.

С целью обеспечения возможности измерения координат точек цифрового изображения с подпиксельной точностью без увеличения исходного изображения разработан метод измерения цифровых изображений, в котором цифровое изображение снимка может смещаться относительно неподвижной измерительной марки с шагом в n – раз меньшим размера пикселя.

Принцип измерения координат точек цифрового изображения по этому методу иллюстрируется на рис.1.4.

Рис. 1.4

На рис.1.4а представлен фрагмент исходного цифрового изображения с измерительной маркой (в виде креста) и точкой изображения m, координаты которой необходимо измерить. Как следует из этого рисунка, центр изображения измерительной марки не совпадает с изображением точки m, причем разности значений их пиксельных координат составляют величины Dx_P и Dy_P.

Для совмещения центра изображения измерительной марки с точкой m можно создать фрагмент цифрового изображения снимка, в котором координаты начала системы координат o’_с x’_с y ’_с будут иметь значения 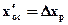, а .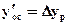

Создание такого фрагмента цифрового изображения производится следующим образом. По координатам центра каждого пикселя фрагмента изображения x’_pi, y’_pi определяют значения координат его проекции x_pi, y_pi в системе координат о_с х_с у_с исходного изображения.

Их значения определяют по формулам:

. (1.6)

Затем по значениям координат x_pi, y_pi находят ближайшие к изображению точки i, соответствующей центру пикселя

Рис. 1.5

создаваемого фрагмента цифрового изображения, четыре пикселя исходного цифрового изображения, например, M, K, L, N (рис.1.5)

Далее методом билинейного интерполирования определяют значения оптической плотности i -го пикселя создаваемого фрагмента изображения по формуле:

, (1.7)

в которой

.

Таким же образом формируются все элементы (пиксели) создаваемого фрагмента цифрового изображения.

На экране дисплея, на визуализированном фрагменте созданного цифрового изображения центр измерительной марки будет совмещен с изображением точки m. Пиксельные координаты точки m изображения в системе координат исходного изображения определяются по формулам 1.6.

Необходимо отметить, что создание фрагмента цифрового изображения требует значительных вычислительных процедур. Поэтому для достижения эффекта перемещения изображения на экране дисплея относительно марки в “реальном масштабе” времени фрагмент изображения не должен иметь большие размеры.

В случае если для измерений используются цветные цифровые изображения при формировании элементов создаваемого изображения методом билинейного трансформирования по формулам (1.7) определяются интенсивности красного (R), зеленого (G) и синего (В) компонентов цветного изображения.

Дата добавления: 2015-05-09