Пример применения логических элементов RS-триггер

Элемент ИЛИ-НЕ

Элемент И-НЕ

Исключающее ИЛИ

Этот логический элемент имеет необычный смысл работы: на выходе появится логический уровень в том случае, если только на одном из входов будет присутствовать логическая единица. Если на оба входа (или на все) подать одинаковые уровни, тогда на выходе уровень не изменится.

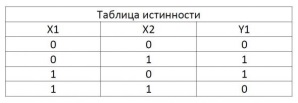
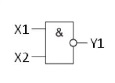
Элемент имеет ту же функцию что и элемент И, но только сигнал на выходе инвертируется. Из таблицы смысл не трудно понять. Это микросхемы серии ЛА: К155ЛА3

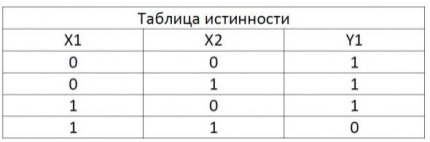
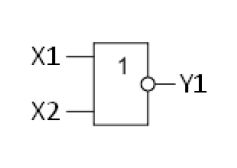
Этот элемент тоже имеет такую функцию, как и элемент ИЛИ. Микросхемы серии ЛЕ: К155ЛЕ1

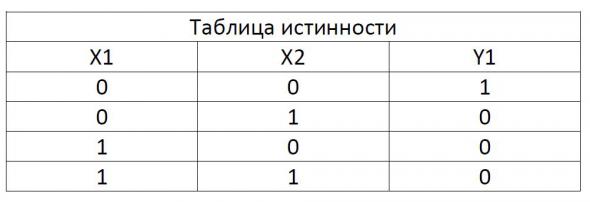
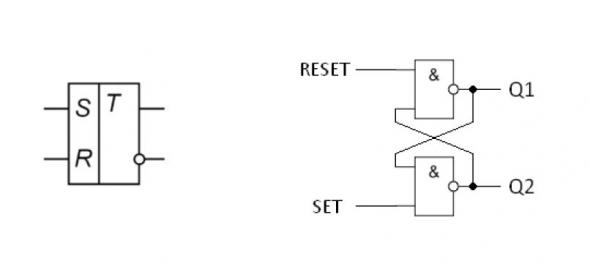
RS триггер – это устройство, которое может устойчиво сохранять одно из двух состояний, или можно сказать «ОЗУ на 1 бит». Q2 это инверсированный Q1 выход. SET установка, RESET сброс. При подаче логического сигнала на RESET, триггер обнуляется, т.е. на Q1 лог. уровень 0. Чтобы триггер перевести в состояние, где из Q1 выходит лог. 1, нужно в момент сброса установить на SET единицу. После прекращения подачи сигнала на RESET, триггер переходит в режим хранения, т.е. триггер запоминает состояние на входе SET.

Двоичные логические операции с цифровыми сигналами (битовые операции)[править | править исходный текст]

Логические операции (булева функция) своё теоретическое обоснование получили в алгебре логики.

Логические операции с одним операндом называются унарными, с двумя — бинарными, с тремя — тернарными (триарными, тринарными) и т. д.

Из 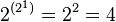возможных унарных операций с унарным выходом интерес для реализации представляют операции отрицания и повторения, причём, операция отрицания имеет большую значимость, чем операция повторения, так как повторитель может быть собран из двух инверторов, а инвертор из повторителей не собрать.

Отрицание, НЕ[править | править исходный текст]

Инвертор, НЕ

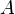
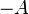
Мнемоническое правило для отрицания звучит так: На выходе будет:

· «1» тогда и только тогда, когда на входе «0»,

· «0» тогда и только тогда, когда на входе «1»

Повторение[править | править исходный текст]

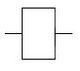
Повторитель (буфер)

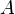
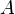
Преобразование информации требует выполнения операций с группами знаков, простейшей из которых является группа из двух знаков. Оперирование с большими группами всегда можно разбить на последовательные операции с двумя знаками.

Из 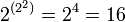возможных бинарных логических операций с двумя знаками c унарным выходом интерес для реализации представляют 10 операций, приведённых ниже.

Конъюнкция (логическое умножение). Операция И[править | править исходный текст]

И

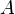
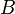
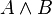
Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:

· «1» тогда и только тогда, когда на всех входах действуют «1»,

· «0» тогда и только тогда, когда хотя бы на одном входе действует «0»

Словесно эту операцию можно выразить следующим выражением: "Истина на выходе может быть при истине на входе 1 И истине на входе 2".

Дизъюнкция (логическое сложение). Операция ИЛИ[править | править исходный текст]

ИЛИ

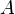
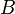
Мнемоническое правило для дизъюнкции с любым количеством входов звучит так: На выходе будет:

· «1» тогда и только тогда, когда хотя бы на одном входе действует «1»,

· «0» тогда и только тогда, когда на всех входах действуют «0»

Инверсия функции конъюнкции. Операция И-НЕ (штрих Шеффера)[править | править исходный текст]

И-НЕ

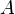
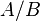
Мнемоническое правило для И-НЕ с любым количеством входов звучит так: На выходе будет:

· «1» тогда и только тогда, когда хотя бы на одном входе действует «0»,

· «0» тогда и только тогда, когда на всех входах действуют «1»

Инверсия функции дизъюнкции. Операция ИЛИ-НЕ (стрелка Пирса)[править | править исходный текст]

ИЛИ-НЕ

		↓

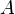
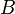
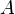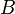
Мнемоническое правило для ИЛИ-НЕ с любым количеством входов звучит так: На выходе будет:

· «1» тогда и только тогда, когда на всех входах действуют «0»,

· «0» тогда и только тогда, когда хотя бы на одном входе действует «1»

Эквивалентность (равнозначность), ИСКЛЮЧАЮЩЕЕ_ИЛИ-НЕ[править | править исходный текст]

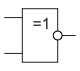
ИСКЛ-ИЛИ-НЕ

		↔

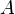
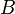
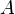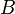
Мнемоническое правило эквивалентности с любым количеством входов звучит так: На выходе будет:

· «1» тогда и только тогда, когда на входе действует четное количество,

· «0» тогда и только тогда, когда на входе действует нечетное количество

Словесная запись: "истина на выходе при истине на входе 1 и входе 2 или при лжи на входе 1 и входе 2".

Сложение (сумма) по модулю 2 (Исключающее_ИЛИ, неравнозначность). Инверсия равнозначности.[править | править исходный текст]

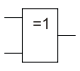
ИСКЛ-ИЛИ

В англоязычной литературе XOR.

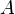
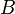
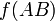
Мнемоническое правило для суммы по модулю 2 с любым количеством входов звучит так: На выходе будет:

· «1» тогда и только тогда, когда на входе действует нечётное количество,

· «0» тогда и только тогда, когда на входе действует чётное количество

Словесное описание: "истина на выходе - только при истине на входе1, либо только при истине на входе 2".

Импликация от A к B (прямая импликация, инверсия декремента, A<=B)[править | править исходный текст]

		→

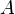
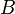
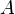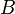
Мнемоническое правило для инверсии декремента звучит так: На выходе будет:

· «0» тогда и только тогда, когда на «B» меньше «А»,

· «1» тогда и только тогда, когда на «B» больше либо равно «А»

Импликация от B к A (обратная импликация, инверсия инкремента, A>=B)[править | править исходный текст]

		→

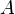
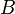
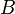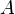
Мнемоническое правило для инверсии инкремента звучит так: На выходе будет:

· «0» тогда и только тогда, когда на «B» больше «А»,

· «1» тогда и только тогда, когда на «B» меньше либо равно «А»

Декремент. Запрет импликации по B. Инверсия импликации от A к B[править | править исходный текст]

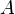
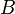
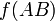
Мнемоническое правило для инверсии импликации от A к B звучит так: На выходе будет:

· «1» тогда и только тогда, когда на «A» больше «B»,

· «0» тогда и только тогда, когда на «A» меньше либо равно «B»

Инкремент. Запрет импликации по A. Инверсия импликации от B к A[править | править исходный текст]

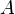
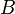
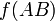
Мнемоническое правило для инверсии импликации от B к A звучит так: На выходе будет:

· «1» тогда и только тогда, когда на «B» больше «A»,

· «0» тогда и только тогда, когда на «B» меньше либо равно «A»

Примечание 1. Элементы импликаций не имеют промышленных аналогов для функций с количеством входов, не равным 2.
Примечание 2. Элементы импликаций не имеют промышленных аналогов.

Этими простейшими логическими операциями (функциями), и даже некоторыми их подмножествами, можно выразить любые другие логические операции. Такой набор простейших функций называется функционально полным логическим базисом. Таких базисов 4:

· И, НЕ (2 элемента)

· ИЛИ, НЕ (2 элемента)

· И-НЕ (1 элемент)

· ИЛИ-НЕ (1 элемент).

Для преобразования логических функций в один из названых базисов необходимо применять Закон (правило) де-Моргана.

Физические реализации[править | править исходный текст]

Реализация логических элементов возможна при помощи устройств, использующих самые разнообразные физические принципы:

· механические,

· гидравлические,

· пневматические,

· электромагнитные,

· электромеханические,

· электронные.

Физические реализации одной и той же логической функции, а также обозначения для истины и лжи, в разных системах электронных и неэлектронных элементов отличаются друг от друга.

Классификация электронных транзисторных физических реализаций логических элементов[править | править исходный текст]

Логические элементы подразделяются и по типу использованных в них электронных элементов. Наибольшее применение в настоящее время находят следующие логические элементы:

· РТЛ (резисторно-транзисторная логика)

· ДТЛ (диодно-транзисторная логика)

· ТТЛ (транзисторно-транзисторная логика)

Упрощённая схема двухвходового элемента И-НЕ ТТЛ.

Обычно входной каскад логических элементов ТТЛ представляет собой простейшие компараторы, которые могут быть выполнены различными способами (на многоэмиттерном транзисторе или на диодной сборке). В логических элементах ТТЛ входной каскад, кроме функций компараторов, выполняет и логические функции. Далее следует выходной усилитель с двухтактным (двухключевым) выходом.

В логических элементах КМОП входные каскады также представляют собой простейшие компараторы. Усилителями являются КМОП-транзисторы. Логические функции выполняются комбинациями параллельно и последовательно включенных ключей, которые одновременно являются и выходными ключами.

Транзисторы могут работать в инверсном режиме, но с меньшим коэффициентом усиления. Это свойство используются в ТТЛ многоэмиттерных транзисторах. При подаче на оба входа сигнала высокого уровня (1,1) первый транзистор оказывается включенным в инверсном режиме по схеме эмиттерного повторителя с высоким уровнем на базе, транзистор открывается и подключает базу второго транзистора к высокому уровню, ток идёт через первый транзистор в базу второго транзистора и открывает его. Второй транзистор «открыт», его сопротивление мало и на его коллекторе напряжение соответствует низкому уровню (0). Если хотя бы на одном из входов сигнал низкого уровня (0), то транзистор оказывается включенным по схеме с общим эмиттером, через базу первого транзистора на этот вход идёт ток, что открывает его и он закорачивает базу второго транзистора на землю, напряжение на базе второго транзистора мало и он «закрыт», выходное напряжение соответствует высокому уровню. Таким образом,таблица истинности соответствует функции 2И-НЕ.

· ТТЛШ (то же с диодами Шоттки)

Для увеличения быстродействия логических элементов в них используются транзисторы Шоттки (транзисторы с диодами Шоттки), отличительной особенностью которых является применение в их конструкции выпрямляющего контакта металл-полупроводник вместо p-n перехода. При работе этих приборов отсутствует инжекция неосновных носителей и явления накопления и рассасывания заряда, что обеспечивает высокое быстродействие. Включение этих диодов параллельно коллекторному переходу блокирует насыщение выходных транзисторов, что увеличивает напряжения логических 0 и 1, но уменьшает потери времени на переключение логического элемента при том же потребляемом токе (или позволяет уменьшить потребляемый ток при сохранении стандартного быстродействия). Так, серия 74хх и серия 74LSxx имеют приблизительно равное быстродействие (в действительности, серия 74LSxx несколько быстрее), но потребляемый от источника питания ток меньше в 4-5 раз (во столько же раз меньше и входной ток логического элемента).

· КМОП (логика на основе комплементарных ключей на МОП транзисторах)

· ЭСЛ (эмиттерно-связанная логика)

Эта логика, иначе называемая логикой на переключателях тока, построена на базе биполярных транзисторов, объединённых в дифференциальные каскады. Один из входов обычно подключён внутри микросхемы к источнику опорного (образцового) напряжения, примерно посредине между логическими уровнями. Сумма токов через транзисторы дифференциального каскада постоянна, в зависимости от логического уровня на входе изменяется лишь то, через какой из транзисторов течёт этот ток. В отличие от ТТЛ, транзисторы в ЭСЛ работают в активном режиме и не входят в насыщение или инверсный режим. Это приводит к тому, что быстродействие ЭСЛ-элемента при той же технологии (тех же характеристиках транзисторов) гораздо больше, чем ТТЛ-элемента, но больше и потребляемый ток. К тому же, разница между логическими уровнями у ЭСЛ-элемента намного меньше, чем у ТТЛ (меньше вольта), и, для приемлемой помехоустойчивости, приходится использовать отрицательное напряжение питания (а иногда и применять для выходных каскадов второе питание). Зато максимальные частоты переключения триггеров на ЭСЛ более, чем на порядок превышают возможности современных им ТТЛ, например, серия К500 обеспечивала частоты переключения 160—200 МГц, по сравнению с 10-15 МГц современной ей ТТЛ серии К155. В настоящее время и ТТЛ(Ш), и ЭСЛ практически не используются, так как с уменьшением проектных норм КМОП технология достигла частот переключения в несколько гигагерц.

Инвертор[править | править исходный текст]

Одним из основных логических элементов является инвертор. Инвертирующими каскадами являются однотранзисторный каскад с общим эмиттером, однотранзисторный каскад с общим истоком, двухтранзисторный двухтактный выходной каскад на комплементарных парах транзисторов с последовательным включением транзисторов по постоянному току (применяется в ТТЛ и КМОП), двухтранзисторный дифференциальный каскад с параллельным включением транзисторов по постоянному току (применяется в ЭСЛ) и др. Но одного условия инвертирования недостаточно для применения инвертирующего каскада в качестве логического инвертора. Логический инвертор должен иметь смещённую рабочую точку на один из краёв проходной характеристики, что делает каскад неустойчивым в середине диапазона входных величин и устойчивым в крайних положениях (закрыт, открыт). Такой характеристикой обладает компаратор, поэтому логические инверторы строят как компараторы, а не как гармонические усилительные каскады с устойчивой рабочей точкой в середине диапазона входных величин. Таких каскадов, как и контактных групп реле, может быть два вида: нормально закрытые (разомкнутые) и нормально открытые (замкнутые).

Применение логических элементов[править | править исходный текст]

Логические элементы входят в состав микросхем, например ТТЛ элементы — в состав микросхем К155 (SN74), К133; ТТЛШ — 530, 533, К555, ЭСЛ — 100, К500 и т. д.

Аналого-цифровые преобразователи (АЦП) предназначены для преобразования аналоговой величины в цифровой код. Другими словами, АЦП - это устройства, которые принимают аналоговые сигналы и генерируют соответствующие им цифровые.

В принципе, вполне реально осуществить преобразование различных физических величин непосредственно в цифровую форму. Однако, процесс этот весьма сложен и кое-где непригоден. Поэтому наиболее рациональным является сначала преобразование чего-то там в функционально связанные с ними электрические сигналы, а затем с помощью преобразователя напряжение-код в цифровые. Именно последние и понимаются, как АЦП.

Сама суть преобразования аналоговых величин заключается в представлении некой непрерывной функции (например, напряжения) от времени в последовательность чисел, отнесенных к неким фиксированным моментам времени. Если говорить простым языком, то пусть, к примеру, есть какой-то сигнал (непрерывный) и для преобразования его в цифровой необходимо этот самый сигнал представить в виде последовательности определенных чисел, каждое из которых относится к определенному моменту времени. Для преобразования аналогового (непрерывного) сигнала в цифровой необходимо выполнить три операции: дискретизация, квантование и кодирование. Во многих умных книжках последняя операция исключается. Об этом немного ниже. Итак, разберем пока непонятные понятия.

Дискретизация - это представление непрерывной функции (т. е. какого-то сигнала) в виде ряда дискретных отсчетов (по-буржуйски дискрет означает отличный, различный). По-другому можно сказать, что дискретизация - это преобразование непрерывной функции в непрерывную последовательность. Давайте глянем на рисунок 1, где изображен принцип дискретизации.

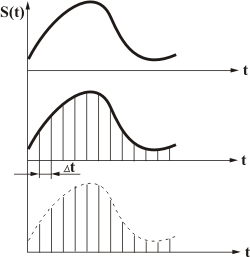
Рис. 1 - Принцип дискретизации

На рисунке показана наиболее распространенная равномерная дискретизация. Сначала имеется непрерывный сигнал S(t). Затем он подвергается разбиению на равные промежутки времени Δt. Вот эти промежутки "дельта тэ" и есть дискретные отсчеты, называемые периодами дискретизации. В результате получается последовательность отсчетов (дискретных) с шагом в Δt. По сути в основе дискретизации непрерывных сигналов лежит возможность представления их, т. е. сигналов в виде взвешенных сумм некоторых коэффициентов, обозначим их как a_i, иначе называемых отсчетами, и набора элементарных функций, обозначим их как f_i(t), используемых при восстановлении сигнала по его отсчетам.

Период дискретизации выбирается из условия:

Δt = 1/2F_в,

где F_в - максимальная частота спектра сигнала. Это выражение есть не что иное, как теорема Котельникова, которая гласит: Любой непрерывный сигнал можно абсолютно точно восстановить на выходе идеального полосового фильтра (ПФ) с полосой F_в, если дискретные отсчеты взяты через интервал Δt = 1 / 2F_в. А это значит, что частота дискретизации должна быть вдвое больше максимальной частоты сигнала. На практике, например, это хорошо иллюстрирует обычный компакт диск (КД или CD) или, как его называют, AudioCD. КД записывают с частотой дискретизации 44,1 кГц. А это значит, что максимальная верхняя частота будет равна 22 кГц, что, как считается, вполне достаточно для уха человека (помните, частотный диапазон для уха человека равен 20...20 000 Гц). Про компакт диски будет отдельная глава.

При квантовании шкала сигнала разбивается на уровни. Отсчеты помещаются в подготовленную сетку и преобразуются в ближайший номер уровня квантования. Опять посморим на рисунок:

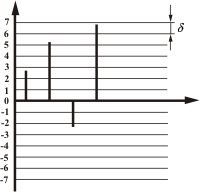
Рис. 2 - Квантование

На рисунке изображено равномерное квантование. Одним из основных параметров является δ - шаг квантования. Соответственно, при равномерном квантовании шаг квантования одинаков. Итак, согласно определению запихиваем отсчеты в подготовленную сетку. Первый (слева направо) отсчет находится ближе к уровню 3 (уровни квантования - по вертикальной оси). Второй - к 5-му уровню и т. п. Таким образом, вместо последовательности отсчетов получаем последовательность чисел, соответствующих уровням квантования.

При равномерном квантовании динамический диапазон получается довольно большим, а это не есть гуд. Поэтому придумали так называемое неравномерное квантование, при котором динамический диапазон уменьшается. Ну понятно, наверное, что шаг квантования δ будет различным при различных уровнях. При малых уровнях сигнала шаг небольшой, при больших он увеличивается. На практике же неравномерное квантование практически не используется. Вместо этого применяют компрессоры, причем америкосы используют μ-компрессоры, европейцы - А-компрессоры (грэческая буковка μ читается "мю"). Характеристика компрессора показана на рисунке 3.

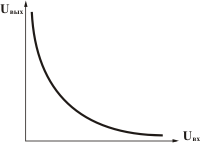
Рис. 3 - Амплитудная характеристика компрессора

Для восстановления ужатого динамического диапазона используют декомпрессор или экспандер. Понятно, что амплитудная характеристика экспандера обратна компрессору.

Кодирование - это сопоставление элементов сигнала с некоторой кодовой комбинацией символов. Широко используется двоичный код.

Ну а теперь перейдем собственно к АЦП. АЦП бывают последовательные и параллельные. Начнем с параллельных.

Дата добавления: 2015-05-09