Цикл Карно. Работа в тепловых машинах (двигатели внутреннего сгорания) осуществляется за счет круговых процессов (циклов)

Работа в тепловых машинах (двигатели внутреннего сгорания) осуществляется за счет круговых процессов (циклов), в которых рабочее тело (газ) получив тепло и совершив работу, возвращается в исходное состояние.

Рассмотрим работу идеальной паровой машины, в которой рабочим телом является 1 моль идеального газа. Цикл такой машины состоит из 4 стадий - процессов: изотермического расширения, адиабатического расширения, изотермического сжатия, адиабатического сжатия. Графически это можно представить как 2 изотермы и 2 адиабаты идеального газа. Все процессы проводятся обратимо.

1 стадия - изотермическое расширение: Газ имеет параметры Р₁,V₁, Т₁. Газ приводится в соприкосновение с нагревателем, имеющим такую же температуру. В результате тепло, поступаемое от нагревателя, не расходуется на повышение внутренней энергии, не теряется зря за счет равенства температур нагревателя и рабочего тела, а расходуется только на совершение работы – работы расширения.

P₁,V₁,T₁ → P₂,V₂,T₁

Тепло, полученное системой, идет на совершение работы:

Q₁ = A₁ = RT₁ln V₂/V₁

2 стадия – адиабатическое расширение: Рабочее тело изолируется от источника, тепло не поступает и не уходит из системы – т.е. без теплообмена, так называемый адиабатический процесс. При этом газ продолжает расширяться. Работа по расширению газа происходит за счет резервов внутренней энергии газа.

А = - ΔU

Внутренняя энергия газа при адиабатическом расширении уменьшается и рабочее тело охлаждается до температуры Т₂.

P₂,V₂,T₁ → P₃,V₃,T₂

При адиабатических процессах:

А₂ = - ΔU = - С_V (T₁-T₂)

3 стадия – изотермическое сжатие: Рабочее тело подается в холодильник, который имеет такую же температуру - Т₂. Опять достигается экономия: теплота не растрачивается зря, т.к. нет переноса тепла, связанного с разностью их температур. Тем не менее. Рабочее тело отдает некоторое количество теплоты Q₂ холодильнику, вследствие чего уменьшается объем рабочего тела до V₄, газ сжимается.

P₃,V₃,T₂ → P₄,V₄,T₂

Процесс сжатия тела необходим для обеспечения цикличности работы машины. Т.к. процесс изотермический, работа равна:

А₃ = - Q₃ = RT₂lnV₄/V₃

4 стадия – адиабатическое сжатие: На четвертой стадии рабочее тело отсоединяют от холодильника, изолируют от внешней среды: газ адиабатически сжимается до первоначального объема. При этом газ нагревается (внутренняя энергия увеличивается) до температуры Т₁. P₄,V₄,T₂ → P₁,V₁,T₁

Работа адиабатического процесса:

А₄ = ΔU = - С_V (T₁-T₂)

Общая работа тепловой машины равна сумме работ на каждой стадии: А = А₁ + А₃ = Q₁ – Q₂

Отсюда:

А = RT₁lnV₂/V₁ - RT₂lnV₄/V₃

Преобразуем уравнение, с учетом, что V₂/V₁ =V₄/V₃:

А = R (T₂ – T₁) ln V₂/V₁ = Q₁ – Q₂

После сокращением получаем:

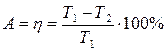
Отсюда еще одна формулировка второго закона термодинамики:

КПД теплового двигателя, работающего по циклу Карно не зависит от природы рабочего газа, а зависит от разности температур нагревателя и холодильника и не может быть равным 100%: вечный двигатель второго рода невозможен.

Все виды энергии могут целиком превращаться в теплоту. Обратный полный переход тепловой энергии в механическую работу невозможен. КПД тепловых двигателей всегда меньше 100%. В этом отношении самыми производительными (КПД = 96%) являются электродвигатели, т.к. электрическая энергия – энергия упорядоченного движения потока электронов, а тепловая энергия – энергия хаотического движения молекул. Само собой беспорядочное движение не может перейти в упорядоченное, поэтому тепловая энергия не может быть полностью превращена в другие виды энергии. Для сравнения: механическая энергия – энергия тоже упорядоченного движения тел.

Все материальные системы обнаруживают тенденцию к достижению максимального беспорядка. Так необратимость процессов характеризуется более вероятностным переходом от порядка к беспорядку, можно ввести количественную меру беспорядка системы – энтропию. Энтропия является функцией определяющей возможность протекания самопроизвольного процесса в изолированной системе

Энтропия (S) - функция состояния, характеризующая меру превращаемости тепла в работу, зависит от температуры и давления.

Второй закон термодинамики через энтропию: В изолированных системах, в которых возможны само­произвольные или необра­тимые процессы, энтропия не может уменьшаться (dS > 0). В этой формулировке заключен критерий самопроизвольности протекания процесса в изолированной системе.

Являясь мерой необратимости процесса энтропия прямо пропорциональна теплоте и обратно пропорциональна температуре:

Мерой превращаемости тепла в работу является функция состояния, зависящая от температуры и давления. Клаузиус (1865 г) предложил назвать эту функцию энтропия - S (от греческого – превращение).

Также как внутренняя энергия и энтальпия энтропия является характеристикой системы, ее функцией состояния. Ее нельзя полностью измерить, и судят только об изменении – ΔS.

Энтропия является количественной мерой беспорядка системы. Единица измерения: ккал/моль*град.

Н₂О _тв → Н₂О_ж ΔS = 30.6 ккал/моль*град

Значение энтропии зависит не только от агрегатного состояния вещества, но и от сложности молекул:

S_CO2 > S_CO ΔS = 16.2 Э.е.

Являясь мерой необратимости процесса энтропия прямо пропорциональна теплоте и обратно пропорциональна температуре:

Изменение энтропии в процессе равно отношению теплового эффекта и абсолютной температуры.

Если процессы протекают 1) самопроизвольно, то

2) в состоянии равновесия

3) в несамопроизвоьных процессах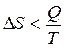

Второй закон термодинамики через энтопию: В изолированных системах, в которых возможны само­произвольные или необра­тимые процессы энтропия не может уменьшаться:

dS > 0

В этой формулировке заключен критерий самопроизвольности протекания процесса в изолированной системе.

Термодинамические потенциалы

Вспомним уравнение первого закона термодинамики:

ΔQ = ΔU + ΔA

Подставив Q =TΔS, получим

TΔS = ΔU + ΔA

Или ΔU = TΔS – ΔA

Рассматривая это уравнение можно заключить, что внутренняя энергия состоит из двух частей. Первая часть – произведенная работа. Эта работа производится системой за счет энергии, которую называют свободной энергией или изобарно-изотермическим потенциалом. В химических процессах протекают одновременно два противоположных процесса: стремление частиц объединиться – что приводит к уменьшению энтропии системы, и стремление частиц к разъединению – увеличение энтропии. Суммарный эффект этих тенденций, протекающих при постоянных температуре и давлении, и отражается в изобарно-изотермическом потенциале или энергии Гибса - ΔG:

ΔG = ΔH – TΔS

В случае изохорно-изотермических процессов T,V =const свободную энергию изохорно-изотермическим потенциалом или энергией Гельмгольца - ΔF:

ΔF = T ΔS - ΔU

Вторая часть внутренней энергии связана с теплотой. Она не переходит в работу, а всегда остается в виде тепла – TΔS. Это связанная энергия – энтропийный фактор. TΔS показывает какое количество теплоты бесполезно рассеяно в самом совершенном двигателе – связанная энергия.

Т.е. по характеру изменений термодинамических функций и энтропии мы можем ответить на вопросы:

1)о принципиальной возможности процесса

2) о направленности процесса

Общий вывод:

1) Если dF < 0, dG < 0, то в системе возможен самопроизвольный процесс без затраты работы и энергии извне. Химическая реакция в этом случае протекает только в одном – прямом направлении.

2) dF > 0, dG > 0 – в этом случае самопроизвольный процесс принципиально невозможен. Химическая реакция в прямом направлении протекает только за счет получения энергии, работы извне.

3) dF = 0, dG = 0 – в этом случае система находится в состоянии равновесия, которое является пределом самопроизвольности процесса при T, P, V = const.

Дата добавления: 2015-05-09