Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами

№2.9

№2.7

№2.6

№2.5

№2.4

№2.3

№2.1

Молекулярная физика и термодинамика.

Задание №1

Задание №2

Задание №3

Задание №4

Задание №5

Задание №6

Задание №7

Задание №8

Задание №9

Задание №10

Задание №11

Задание №12

Задание №13

Задание №14

Задание №15

Задание №16

Задание №17

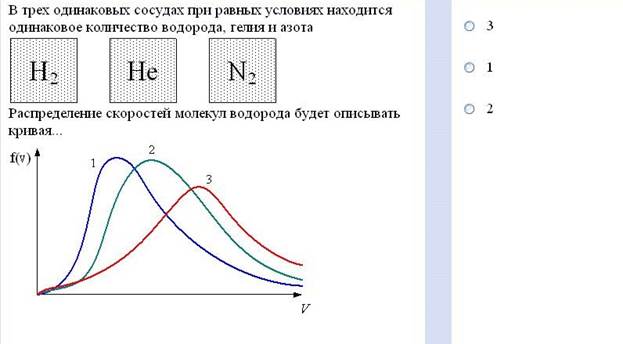
Задание №18

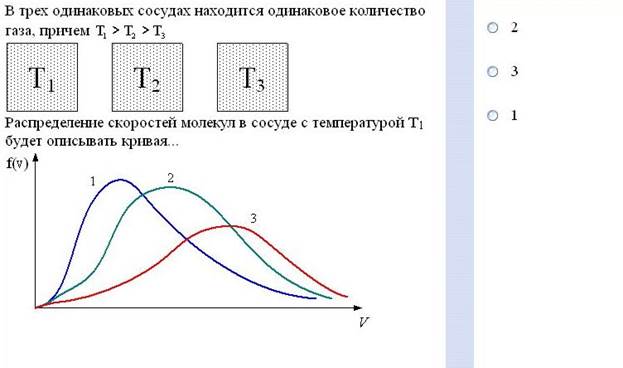
Задание №19

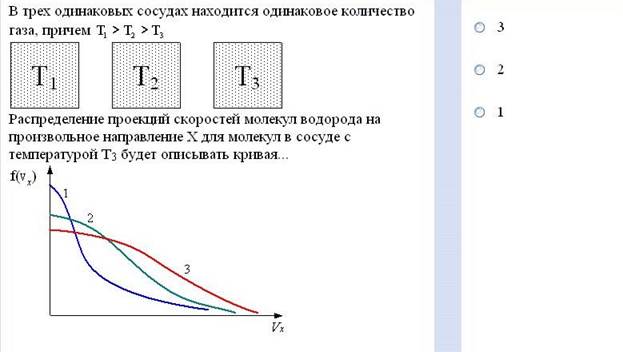
Задание №20

Задание №21

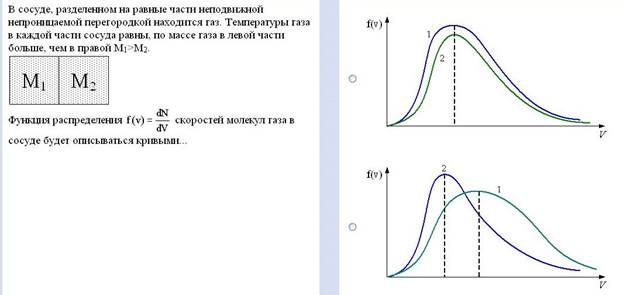
Задание №22

Задание №23

Задание №24

Задание №25

Задание №26

Задание №27

Статистический метод — это метод исследования систем из большого числа частиц, оперирующий статистическими закономерностями и средними (усредненными) значениями физических величин, характеризующих всю систему. Термодинамический метод — это метод исследования систем из большого числа частиц, оперирующий величинами, характеризующими систему в целом (например, давление, объем, температура) при различных превращениях энергии, происходящих в системе, не учитывая при этом внутреннего строения изучаемых тел и характера движения отдельных частиц. Молекулярная физика — раздел физики, изучающего строение и свойства вещества исходя из молекулярно-кинетических представлений, основывающихся на том, что все тела состоят из атомов, молекул или ионов находящихся в непрерывном хаотическом движении. термодинамическая система — совокупность макроскопических тел, которые взаимодействуют и обмениваются энергией как между собой, так и с другими телами (внешней средой). Любое изменениев термодинамической системе, связанное с изменением хотя бы одного из ее термодинамических параметров, называется термодинамическим процессом. Состояние системы задается термодинамическими параметрами (параметрами состояния) — совокупностью физических величин, характеризующих свойства термодинамической системы. Обычно в качестве параметров состояния выбирают температуру, давление и объем. Уравнением состояния термодинамической системы называется уравнение, которое связывает давление p, объем V и температуру T термодинамической системы, находящейся в состоянии термодинамического равновесия. Идеальный газ - это газ, в котором отсутствуют силы межмолекулярного взаимодействия, т. е. молекулы считаются упругими твердыми шариками соударения между которыми абсолютно упругие, силы притяжения межу ними отсутствуют. Физическая модель, идеального газа 1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда; 2) между молекулами газа отсутствуют силы взаимодействия; 3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие. Закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений n входящих в нее газов. Парциальное давление — давление, которое производил бы газ, входящий в состав газовой смеси, если бы он один занимал объем, равный объему смеси при той же температуре. Закон Бойля-Мариотта: Для данной массы газа m при постоянной температуре T произведение давления p на объем V есть величина постоянная: PV=const. Закон Гей-Люссака: Давление p данной массы m газа при постоянном объеме изменяется линейно с температурой t. Объем V данной массы m газа при постоянном давлении изменяется линейно с температурой t.

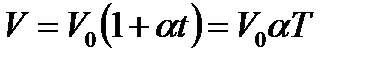
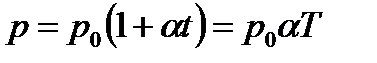
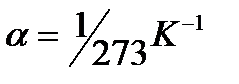
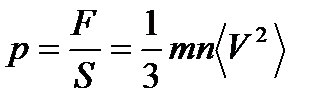
Основное:

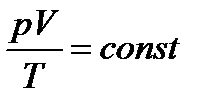
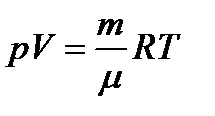Температура: физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы и определяющая направление теплообмена между телами. Уравнение состояния идеального газа:

Уравнение Менделеева-Клапейрона:

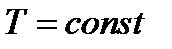Изотермический:

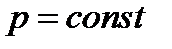
Изобарный:

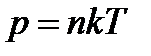
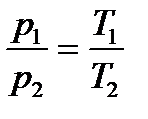
Изохорный:

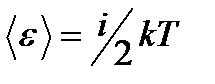
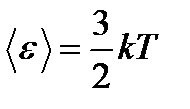№2.2

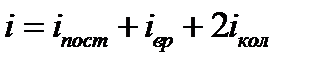
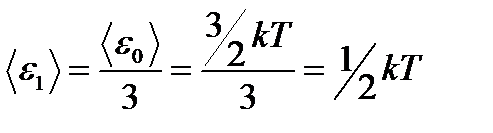Средняя: Для системы, находящейся в состоянии термодинамического равновесия на каждую поступательную и вращательную степень свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень свободы — в среднем энергия, равная kT.

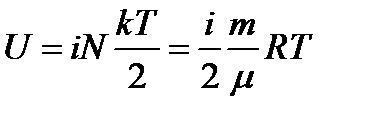Внутренняя энергия идеального газа, содержащего N не взаимодействующих молекул (общее число степеней свободы iN):

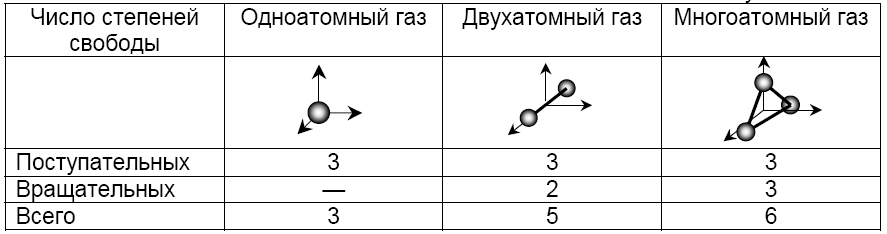
Внутренней энергией тела называют часть его полной энергии за вычетом кинетической энергии движения тела как целого и потенциальной энергии тела во внешнем поле. Таким образом, во внутреннюю энергию входят кинетическая энергия поступательного и вращательного движений молекул, потенциальная энергия их взаимодействия, энергия колебательного движения атомов в молекулах, а также энергия различных видов движения частиц в атомах.

Частные случаи:

Если, то это означает, что тепло к системе подводится.

Если, 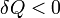аналогично — тепло отводится.

Если, то система не обменивается теплом с окружающей средой и называется адиабатически изолированной.

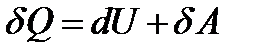Количество энергии, передаваемой системе внешними телами в форме теплоты, называется количеством теплоты или теплотой Q сообщаемой передаваемой системе. Первое начало термодинамики – это закон сохранения и превращения энергии в термодинамических процессах.: теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил.

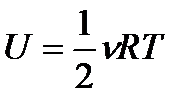
Изотермический:

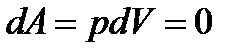
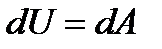
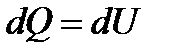
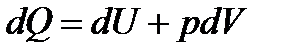Изобарный: Изохорный: Адиабата:

Изотермический:

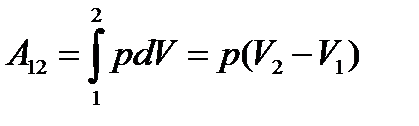
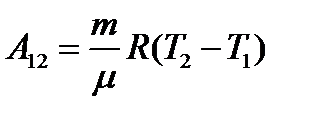
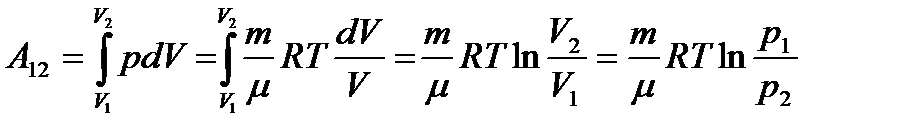
Изобарный:

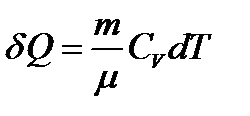
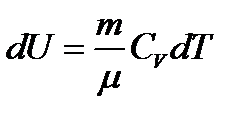
Изохорный:

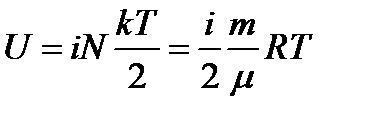Внутренняя энергия идеального газа, содержащего N не взаимодействующих молекул (общее число степеней свободы iN):

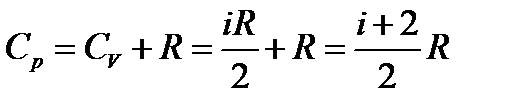
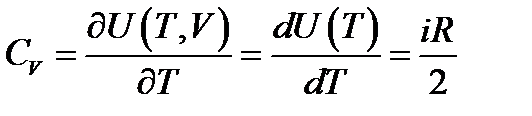Теплоемкость идеального газа в классической теории не зависит от температуры. В экспериментах соответствует только одноатомным газам.

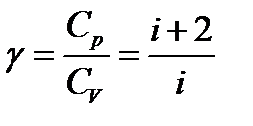
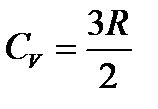
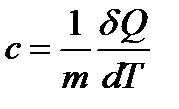
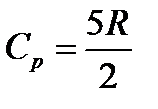
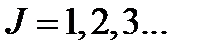
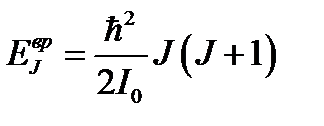
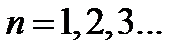
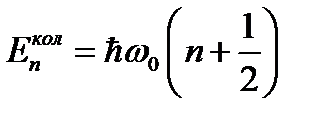Молярная теплоемкость C — величина, равная количеству теплоты, необходимому для нагревания 1моль вещества на 1К. Единица молярной теплоемкости — Дж/(моль К). Удельная теплоемкость вещества c: величина, равная количеству теплоты, необходимому для нагревания 1кг вещества на 1К. Единица удельной теплоемкости — Дж/(кг К).

Тепловая энергия сравнима с квантом колебательной

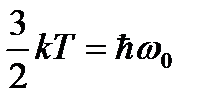
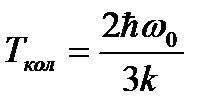
энергии:

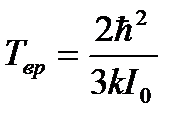
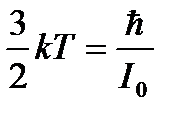
Тепловая энергия сравнима с квантом вращательной энергии:

КЛАССИЧЕСКАЯ ТЕОРИЯ ТЕПЛОЕМКОСТИ Эта теория основывается на предположении о равномерном распределении энергии по степеням свободы движения молекулы. Молекула идеал. однотомного газа, рассматриваемая как мат. точка, может иметь только энергию поступательного движения. Энергией вращательного движения такая молекула не обладает вследствие того, что при соударениях молекул идеального одноатомного газа энергия вращательного движения не передается.

Теорема Больцмана — Максвелла утверждает далее, что такое же количество внергии приходится на одну степень свободы в любом газе, независимо от числа степеней свободы, которыми обладает молекула этого газа. Поэтому задача о вычислении энергии газовой молекулы, а следовательно, и об определении его теплоемкости, сводится к определе- определению числа степеней свободы газовой молекулы.

Число степеней свободы в сложных молекулах может быть значительно больше шести, так как имеются многочисленные степени свободы колебательного движения атомов. Каждое колебательное движение в молекулы дает две степени свободы: одна из них соответствует кинетической энергии молекулы, другая — потенциальной.

Трудности классической теории:

1. Даже при "Комнатных" температурах теплоемкости разных газов с одинаковым количеством атомов отличаются друг от друга, и не кратны R.

2. Согласно Кл. теории С газов не должно зависеть от T, на самом деле С сильно понижается с понижением Т.

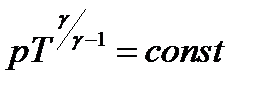
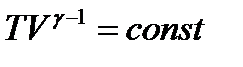
Адиабатическим называется процесс, при котором отсутствует теплообмен между системой и окружающей средой (δQ = 0). Уравнения Пуассона:

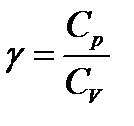
Коэффициент Пуассона:

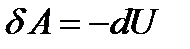Закон:

Процесс, в котором теплоемкость остается постоянной называется политропическим.

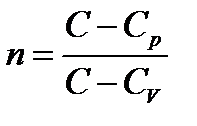
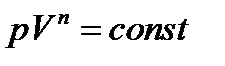Уравнение политропы: Показатель политропы:

Адиабатическим называется процесс, при котором отсутствует теплообмен (δQ=0) между системой и окружающей средой. Адиабатическим процессами можно считать все быстропротекающие процессы. Таковым, например, можно считать процесс распространения звука в среде, так как скорость распространения звуковой волны настолько большая по значению, что обмен энергией между средой и волной произойти не успевает. Адиабатические процессы происходят в двигателях внутреннего сгорания (сжатие и расширение горючей смеси в цилиндрах), в холодильных установках и т. д.

Состояние газа характеризуется p, V, T: макроскопическими параметрами. Описание системы внешними и внутренними параметрами. Внутренние параметры: состояние молекул газа. Состояние системы характеризующиеся положением и скоростями всех её молекул: микроскопическая. Статистическим ансамблем физической системы называется набор всевозможных состояний данной системы, отвечающих определённым критериям. Микроканонический ансамбль, описывающий состояния системы с заданными (постоянными) энергией, импульсом и моментом импульса системы.

Постулат равновероятности: все микроскопические состояния системы равновероятны. Эргодическая гипотеза: средняя величина, характеризующая частицу рассчитанная по числу её возможных состояний равна среднему значению этой величины усреднённому за достаточно большой промежуток времени. Термодинамическая вероятность состояния тела или системы: это число способов, которыми может быть реализовано данное конкретное термодинамическое состояние (макросостояние). Иначе говоря, это число всевозможных микрораспределений частиц по координатам и скоростям (микросостояний), которыми может быть осуществлено данное макросостояние.

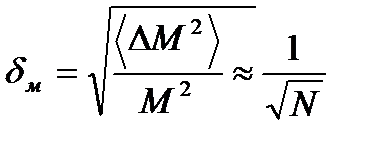где Г_о- число возможных микросостояний. Флуктуации — случайные отклонения от среднего значения физических величин, характеризующих систему из большого числа частиц. Можно показать, что чем больше частиц в системе, тем большие флуктуации менее вероятны:

где М- число частиц в системе.

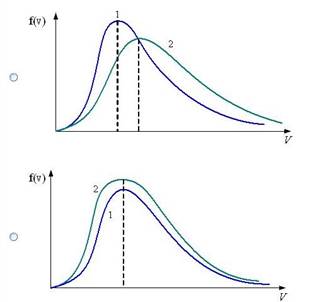
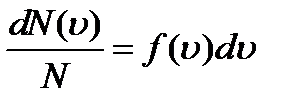Распределение вероятностей — это закон, описывающий область значений случайной величины и вероятности их принятия. В газе, находящемся в состоянии равновесия при данной температуре, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям. Это распределение описывается функцией f (v), называемой функцией распределения молекул по скоростям:

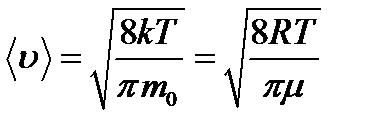
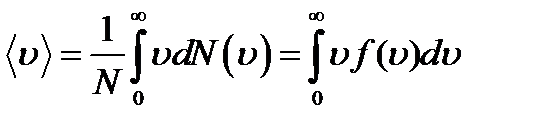Средняя скорость молекулы газа:

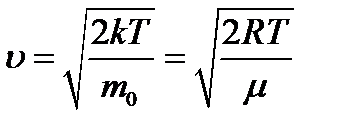Наиболее вероятная скорость молекул идеального газа:

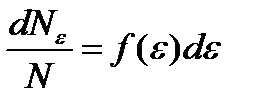
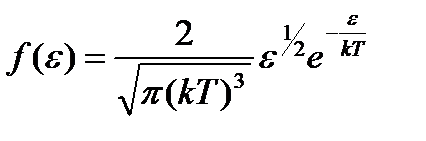
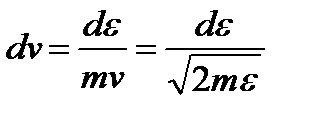
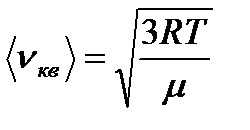
Средняя квадратичная скорость:

Распределение Ма́ксвелла — распределение вероятности, встречающееся в физике и химии. Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и диффузию. Распределение Максвелла также применимо для электронных процессов переноса и других явлений. Распределение Максвелла применимо к множеству свойств индивидуальных молекул в газе. О нём обычно думают как о распределении энергий молекул в газе, но оно может также применяться к распределению скоростей, импульсов, и модуля импульсов молекул. Также оно может быть выражено как дискретное распределение по множеству дискретных уровней энергии, или как непрерывное распределение по некоторому континууму энергии.

Распределение Максвелла может быть получено при помощи статистической механики (см. происхождение статсуммы). Как распределение энергии, оно соответствует самому вероятному распределению энергии, в столкновительно-доминируемой системе, состоящей из большого количества невзаимодействующих частиц, в которой квантовые эффекты являются незначительными. Так как взаимодействие между молекулами в газе является обычно весьма небольшим, распределение Максвелла даёт довольно хорошее приближение ситуации, существующей в газе.

Во многих других случаях, однако, даже приблизительно не выполнено условие доминирования упругих соударений над всеми другими процессами. Это верно, например, в физике ионосферы и космической плазмы, где процессы рекомбинации и столкновительного возбуждения (то есть излучательные процессы) имеют большое значение, в особенности для электронов. Предположение о применимости распределения Максвелла дало бы в этом случае не только количественно неверные результаты, но даже предотвратило бы правильное понимание физики процессов на качественном уровне. Также, в том случае где квантовая де Бройлева длина волны частиц газа не является малой по сравнению с расстоянием между частицами, будут наблюдаться отклонения от распределения Максвелла из-за квантовых эффектов.

Распределение энергии Максвелла может быть выражено как дискретное распределение энергии:

,

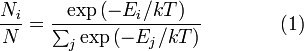
где является числом молекул имеющих энергию при температуре системы, является общим числом молекул в системе и — постоянная Больцмана. (Отметьте, что иногда вышеупомянутое уравнение записывается с множителем, обозначающим степень вырождения энергетических уровней. В этом случае сумма будет по всем энергиям, а не всем состояниям системы). Поскольку скорость связана с энергией, уравнение (1) может использоваться для получения связи между температурой и скоростями молекул в газе. Знаменатель в уравнении (1) известен как каноническая статистическая сумма.

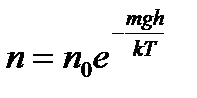
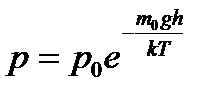№2.8

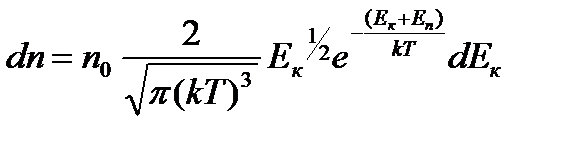Формула:: такое распределение называют распределением Больцмана (распределение частиц по значениям потенциальной энергии) для внешнего потенциального поля. Распределение Максвелла-Больцмана: где dn: количество молекул в единице объёма, и имеющих Е_п, а Е_к лежит в интервале от Е_к до Е_к+dЕ_к . Если частицы имеют одинаковую массу и находятся в состоянии хаотического теплового движения, то распределение Больцмана справедливо в любом внешнем потенциальном поле, а не только в поле сил тяжести.

Распределение Больцмана — распределение вероятностей различных энергетических состояний идеальной термодинамической системы (идеальный газ атомов или молекул) в условиях термодинамического равновесия; открыто Л. Больцманом в 1868—1871.

Согласно распределению Больцмана среднее число частиц с полной энергией Ei равно

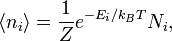
где Ni — кратность состояния частицы с энергией Ei — число возможных состояний частицы с энергией Ei. Постоянная Z находится из условия, что сумма ni по всем возможным значениям i равна заданному полному числу частиц n в системе (условие нормировки):

∑ni = n.

i

В случае, когда движение частиц подчиняется классической механике, энергию Ei можно считать состоящей из

кинетической энергии 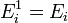(кин) частицы (молекулы или атома),

внутренней энергии (вн) (например, энергии возбуждения электронов) и

потенциальной энергии 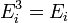(пот) во внешнем поле, зависящей от положения частицы в пространстве:

Дата добавления: 2015-05-09