Гипотеза де Бройля. Волновые свойства вещества

Энергия, масса и импульс фотона

Фотон обладает энергией Е = hv. Согласно теории отно­сительности, частица с энергией Е обладает массой m = Е/С². Фотон — частица, движущаяся со скоростью света С. При движении фотона его масса, как видно из приведенных формул, конечна. Однако подстановка в фор­мулы специальной теории относительности значения ско­рости движущегося объекта V=C приведет к равенству нулю массы покоя фотона. То есть фотон существенно от­личается от обычных известных к тому времени в физике частиц, так как не имеет массы покоя и может существо­вать только в движении. Из равенства вышеприведенных формул получим:

Импульс фотона Р = mС и, следовательно, равен:

где 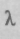— длина волны.

Основополагающей в квантовой механике является идея о том, что корпускулярно-волновая двойственность свойств, установленная для света, имеет универсальный характер. В 1924 году Луи де Бройль распространил идею о двойственной корпускулярно-волновой природе света на

все материальные объекты, введя представление о волнах, названных волнами де Бройля. Все частицы, обладающие конечным импульсом Р, обладают волновыми свойствами, и их движение сопровождается некоторым волновым про­цессом. Де Бройль, исходя из общих принципов теории относительности, получил закон, устанавливающий зависи­мость длины волны, связанной с движущейся частицей, от импульса частицы:

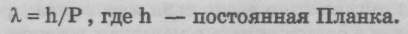
Вид зависимости полностью совпал с соотношением для фотона и связанной с ним световой волной. Как от­мечал сам автор идеи: «Так был осуществлен знаменитый синтез, ибо оказалось, что для частиц материи и для све­та установлен один и тот же вид дуализма». Однако воз­никает вопрос, если с какой-либо движущейся частицей, скажем, с движущимся электроном, связана волна, то дол­жны проявляться эффекты, определяемые волновыми свой­ствами электрона, например, дифракция электронов? Еще за несколько лет до опубликования статьи де Бройля К.Дж. Дэвиссон со своими коллегами по лаборатории «Белл те­лефон» экспериментально исследовали явления испускания вторичных электронов и получили непонятные результа­ты, которые тогда они не смогли объяснить. После опуб­ликования статьи де Бройля Дэвиссон и его сотрудник Л. Джермер возобновили опыты и установили, что элект­роны дифрагируют на кристаллах как волны, и длина этих волн полностью соответствует формуле де Бройля. Впослед­ствии экспериментальная проверка дифракции электронов была многократно повторена. В настоящее время во мно­гих университетах этот эксперимент используют в качест­ве демонстрационного материала при чтении лекций по квантовой физике. Позже были проведены эксперименты, устанавливающие дифракцию других элементарных час­тиц и даже атомов. Итак, сомнений в волново-корпуску­лярном дуализме частиц нет, но есть ли понимание это­го явления? Наверное, ситуация немного прояснится, если рассмотреть опыт с двумя щелями, подробно описанный Р. Фейнманом. «Я разберу только этот эксперимент, — пи­шет Р. Фейнман на странице 118 книги «Характер физи­ческих законов», — который специально придуман таким

образом, чтобы охватить все загадки квантовой механики и столкнуть нас со всеми парадоксами, секретами и стран­ностями природы на все сто процентов. Оказывается, что любой другой случай в квантовой механике всегда можно объяснить, сказав: «Помните наш эксперимент с двумя отверстиями? Здесь — то же самое». Интересующегося чи­тателя мы отсылаем к вышеназванной книге для более глубокого проникновения в суть результатов опыта, рас­смотренного Фейнманом для объяснения квантовой меха­ники. Мы же вкратце прокомментируем его результаты.

Фейнман рассматривает три случая прохождения через экран с двумя отверстиями различных объектов.

Случай 1. Пусть имеется источник с пулями, перед ко­торым установлен броневой щит с одним отверстием, про­пускающим пули. На большом расстоянии от первого щита поставим второй, уже с двумя отверстиями. До­статочно далеко от второго щита будет установлен третий щит, в котором пули, прошедшие через отверстия, будут застревать — так, что их можно будет сосчитать. Сразу можно обратить внимание на то, что пули представляют собой дискретные порции энергии. Предположим, что вся энергия движения пули полностью переходит во внутрен­нюю энергию мишени. Ясно, что энергия мишени при по­падании в нее пули увеличивается скачком на величину энергии одной пули, то есть дискретными порциями. Каж­дая пуля — одна нерасчленяемая и опознаваемая порция, поэтому если в качестве мишени использовать ящики с песком, расположенные вдоль поверхности последнего щита, то одна пуля может попасть только в один из ящи­ков. Если второе отверстие закрыть броневой завесой, то пули могут достичь мишени только через первое отверстие. При этом большая часть пролетевших пуль будет попадать в ящик с песком, находящимся прямо напротив этой щели. Число прошедших пуль за определенную единицу времени легко сосчитать. Скажем, это будет значение N_1. Теперь закроем первое отверстие, получим число пуль N₂, прошед­ших через второе отверстие. Если будут открыты оба от­верстия, то окажется, что число прошедших через обе щели пуль N₁₂ представляет собой простую сумму N₁ и N₂. Этот факт не является для нас поразительным, именно это мы и ожидали получить. Учитывая, что пули — это дискрет-

ные порции веществ, — частицы, а не волны, «отсутствие интерференции» в опыте находится в полном соответствии с нашим обыденным опытом.

Случай 2. Здесь через отверстия будут пропускаться волны, например, морские. Броневые щиты заменяют на дамбу с двумя проходами для воды. Оказывается в случае, если оба прохода будут открыты сразу, наблюдается явле­ние интерференции — явление перераспределения гребней и впадин в пространстве за дамбой вследствие наложения волн, проходящих через первый проход и через второй про­ход, друг на друга. Интенсивность суммарной волны уже не будет равна сумме интенсивностей волн, проходящих через первый проход (при закрытом втором проход) и че­рез второй проход (при закрытом первом проходе):

Здесь под величиной I понимается интенсивность вол­ны — величина, характеризующая энергию волны. Поло­жение максимумов интенсивностей, то есть гребни резуль­тирующей волны за дамбой, может быть достаточно легко рассчитано. Но что интересно: вовсе не обязательно, что они будут располагаться прямо напротив проходов.

Различие между корпускулами и волнами очевидно.

Случай 3. Теперь поэкспериментируем с электронами. Пусть у нас имеется источник с электронами, экран с дву­мя отверстиями и детектор, стоящий за экраном и способ­ный регистрировать заряд, приносимый электроном. При попадании электронов в детектор происходит щелчок. Мы легко установим по щелчкам, что электроны попадают в детектор дискретно, строго по одному, порциями. Следова­тельно, можно поступать так же, как и в случае с пулями: можно измерять вероятность появления электронов в каж­дой точке экрана. Экспериментально установлено, что если оба отверстия будут открыты, то мы получим кривую ве­роятности попадания, соответствующую кривой, получен­ной в опыте с интерференцией волн. Если поочередно за­крывать то одно отверстие, то другое, а при этом снимать кривые вероятности попадания одной дискретной порции в детектор, то мы получим значения N₁ и N₂, но вероят­ность попадания при условии, когда открыты оба отверстия, уже не равна их сумме:

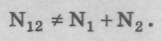
Электроны попадают в детектор дискретными порция­ми, как если бы это были частицы, но вероятности попа­дания этих частиц определяются по тем же законам, по которым определяется интенсивность волнения воды.

Теперь обратим внимание на следующее важное обсто­ятельство: когда были открыты оба отверстия, вследствие чего была получена интерференционная картина, мы не следили за тем, через какое из двух отверстий в данный момент пролетает электрон. Изменим экспериментальную ситуацию таким образом, чтобы можно было следить за этим. Поэтому за отверстиями помещают мощный источ­ник света: электроны рассеивают свет, и по вспышке за отверстием 1 или 2 можно точно установить, через какое из них пролетел электрон. При такой постановке экспери­мента мы получаем совершенно другой результат: интер­ференционная картина разрушается, и поведение электро­нов совпадает с поведением пуль в первом рассмотренном нами случае, так что N₁₂ = N₁ + N₂. И какие бы усовер­шенствования в постановке экспериментов не были бы предложены, каждый раз оказывается, что невозможно, с од­ной стороны, сказать, через какое отверстие пролетает наш электрон, то есть точно определить его координату, а с дру­гой стороны — не исказить картины распределения реги­стрируемых электронов, не нарушить характера интерферен­ции. По интерференционной картине всегда можно опреде­лить длину волны электронов, а затем по формуле де Бройля импульс электрона. Но в этом случае оказывает­ся, что мы знаем импульс электрона, но не знаем его ко­ординату, так как не определяли, через какое отверстие прошел электрон. И наоборот, если мы знаем координату электрона, то ничего не можем сказать об импульсе вслед­ствие разрушения интерференционной картины. В разных экспериментальных ситуациях электрон ведет себя по-раз­ному: в одних — как частица, а в других — как волна. Этот совершенно неожиданный, с точки зрения классичес­кой физики, результат был выражен в принципе неопреде­ленности Гейзенберга и принципе дополнительности Бора.

Дата добавления: 2015-05-07